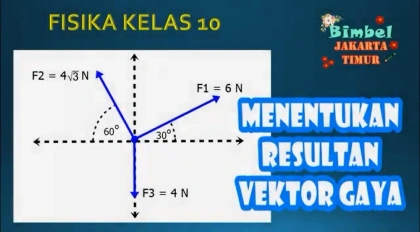
Menentukan Resultan Vektor Gaya
Pengantar
Dalam dunia fisika, vektor gaya merupakan konsep penting yang sering digunakan untuk menggambarkan dan menganalisis berbagai fenomena. Vektor gaya adalah besaran vektor yang mewakili gaya yang bekerja pada suatu benda. Setiap vektor gaya memiliki besaran (magnitude) dan arah. Ketika beberapa vektor gaya bekerja pada suatu benda, kita perlu menentukan resultan atau jumlah total dari vektor-vektor tersebut.
Menentukan resultan vektor gaya sangat berguna dalam berbagai aplikasi, seperti analisis struktur, mekanika benda rigid, dan dinamika partikel. Dengan mengetahui resultan vektor gaya, kita dapat memahami arah dan besaran gaya total yang bekerja pada suatu benda, sehingga dapat membuat keputusan yang tepat dalam perancangan atau analisis.
Dalam artikel ini, kita akan membahas bagaimana menentukan resultan vektor gaya, baik secara grafis maupun secara matematis. Kita juga akan melihat contoh-contoh penerapannya dalam berbagai situasi.
Menentukan Resultan Vektor Gaya Secara Grafis
Salah satu cara untuk menentukan resultan vektor gaya adalah dengan menggunakan metode grafis. Metode ini melibatkan penggambaran vektor-vektor gaya pada sebuah diagram, kemudian menentukan resultan vektor gaya secara geometris.
Berikut adalah langkah-langkah untuk menentukan resultan vektor gaya secara grafis:
Gambarkan vektor-vektor gaya: Pertama, gambarkan vektor-vektor gaya yang bekerja pada benda dengan memperhatikan besaran dan arah masing-masing vektor. Biasakan untuk memilih skala yang sesuai agar diagram terlihat jelas.
Susun vektor-vektor gaya: Susun vektor-vektor gaya tersebut sedemikian rupa sehingga ekor (pangkal) vektor yang satu berhimpit dengan ujung vektor yang lain. Hal ini disebut sebagai penjumlahan vektor secara grafis.
Gambarkan resultan vektor gaya: Tarik garis lurus dari ekor vektor pertama hingga ujung vektor terakhir. Garis ini merepresentasikan resultan vektor gaya, baik dalam besaran maupun arahnya.
Dengan mengikuti langkah-langkah di atas, kita dapat dengan mudah menentukan resultan vektor gaya secara grafis. Metode ini sangat berguna terutama untuk masalah-masalah sederhana dengan sedikit vektor gaya yang bekerja.
Menentukan Resultan Vektor Gaya Secara Matematis
Selain metode grafis, kita juga dapat menentukan resultan vektor gaya secara matematis. Metode ini melibatkan perhitungan matematis berdasarkan komponen-komponen vektor gaya.
Misalkan ada dua vektor gaya, F1 dan F2, yang membentuk sudut θ satu sama lain. Untuk menentukan resultan vektor gaya (R) secara matematis, kita dapat menggunakan rumus berikut:
R = √(F1^2 + F2^2 + 2F1F2cos(θ))
di mana:
- R adalah besaran resultan vektor gaya
- F1 dan F2 adalah besaran masing-masing vektor gaya
- θ adalah sudut antara kedua vektor gaya
Selain itu, kita juga dapat menentukan arah resultan vektor gaya (α) menggunakan rumus:
tan(α) = F2sin(θ) / (F1 + F2cos(θ))
di mana:
- α adalah arah resultan vektor gaya
Dengan menggunakan rumus-rumus ini, kita dapat menghitung resultan vektor gaya secara matematis, bahkan untuk kasus-kasus yang lebih kompleks dengan lebih dari dua vektor gaya.
Contoh Penerapan
Untuk memahami lebih jelas, mari kita lihat beberapa contoh penerapan dalam menentukan resultan vektor gaya.
Contoh 1: Dua Vektor Gaya yang Membentuk Sudut
Misalkan ada dua vektor gaya, F1 = 10 N dan F2 = 15 N, yang membentuk sudut 60 derajat satu sama lain. Tentukan resultan vektor gaya (R) dan arahnya (α).
Penyelesaian:
Menggunakan rumus untuk menentukan besaran resultan vektor gaya: R = √(F1^2 + F2^2 + 2F1F2cos(θ)) R = √(10^2 + 15^2 + 2 × 10 × 15 × cos(60°)) R = √(100 + 225 + 300) R = √625 R = 25 N
Menggunakan rumus untuk menentukan arah resultan vektor gaya: tan(α) = F2sin(θ) / (F1 + F2cos(θ)) tan(α) = 15sin(60°) / (10 + 15cos(60°)) tan(α) = 13 / 22 α = arctan(13/22) α = 30,96 derajat
Jadi, resultan vektor gaya (R) adalah 25 N dan arahnya (α) adalah 30,96 derajat.
Contoh 2: Tiga Vektor Gaya yang Membentuk Sudut
Misalkan ada tiga vektor gaya, F1 = 8 N, F2 = 12 N, dan F3 = 6 N, yang membentuk sudut 30 derajat, 45 derajat, dan 60 derajat satu sama lain. Tentukan resultan vektor gaya (R) dan arahnya (α).
Penyelesaian:
Langkah pertama adalah menggambarkan vektor-vektor gaya tersebut secara grafis.
Selanjutnya, kita dapat menentukan resultan vektor gaya (R) secara matematis: R = √(F1^2 + F2^2 + F3^2 + 2F1F2cos(30°) + 2F1F3cos(60°) + 2F2F3cos(45°)) R = √(8^2 + 12^2 + 6^2 + 2 × 8 × 12 × cos(30°) + 2 × 8 × 6 × cos(60°) + 2 × 12 × 6 × cos(45°)) R = √(64 + 144 + 36 + 192 + 96 + 144) R = √676 R = 26 N
Untuk menentukan arah resultan vektor gaya (α), kita dapat menggunakan rumus: tan(α) = (F2sin(45°) + F3sin(60°)) / (F1 + F2cos(45°) + F3cos(60°)) tan(α) = (12sin(45°) + 6sin(60°)) / (8 + 12cos(45°) + 6cos(60°)) tan(α) = (12 × 0,707 + 6 × 0,866) / (8 + 12 × 0,707 + 6 × 0,5) tan(α) = 15,852 / 22,242 α = arctan(15,852/22,242) α = 35,38 derajat
Jadi, resultan vektor gaya (R) adalah 26 N dan arahnya (α) adalah 35,38 derajat.
Kesimpulan
Menentukan resultan vektor gaya merupakan kemampuan penting dalam bidang fisika dan teknik. Dengan memahami konsep ini, kita dapat menganalisis dan memahami gaya-gaya yang bekerja pada suatu benda.
Dalam artikel ini, kita telah mempelajari dua metode untuk menentukan resultan vektor gaya, yaitu secara grafis dan secara matematis. Metode grafis membantu kita memvisualisasikan vektor-vektor gaya dan menentukan resultan secara geometris. Sementara itu, metode matematis menggunakan rumus-rumus untuk menghitung besaran dan arah resultan vektor gaya.
Dengan mempraktikkan contoh-contoh yang diberikan, Anda dapat semakin mahir dalam menentukan resultan vektor gaya dan menerapkannya dalam berbagai situasi. Pemahaman yang baik tentang konsep ini akan membantu Anda dalam memecahkan masalah-masalah fisika dan teknik yang melibatkan vektor gaya.