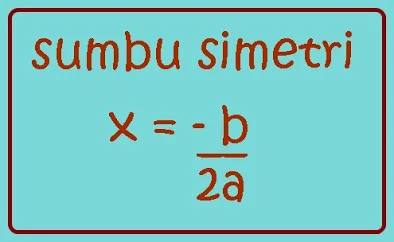Grafik Fungsi Kuadrat By Bimbel Jakarta Timur

Fungsi kuadrat yaitu fungsi yang persamaannya memiliki variabel dengan pangkat tertingginya 2. Dalam materi fungsi kuadrat kita pelajari ciri-ciri grafik fungsi kuadrat,sumbu simetri, nilai optimum (maksimum atau minimum) serta titik potongnyaterhadap sumbu pada koordinat kartesius. 

Persamaan umumfungsi kuadrat adalah :

F(x)=ax² + bx + c atau y=ax² + bx + c

Variabel x padafungsi kuadrat adalah variabel bebas sedangkan y sebagai variabel terikat. adan b sebagai koefisien dimana a ≠ 0  danc sebagai konstanta.

Grafik fungsi kuadrat adalah grafik berbentuk kurva parabola yangdihasilkan dari persamaan kuadrat yang digambarkan pada bidang kartesius.

Sifat-sifat grafik fungsi kuadrat

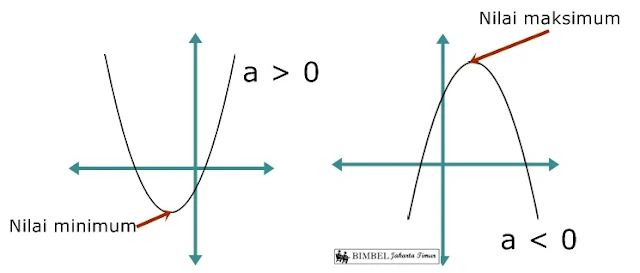
1. Nilai a

- Jika nilai a> 0, maka parabola akan terbuka ke atas. Pada grafik ini, titik puncakparabola berada di bawah sehingga menghasilkan nilai minimum.

- Jika nilai a< 0, maka parabola akan terbuka ke bawah. Pada grafik ini, titik puncakparabola berada di bawah sehingga menghasilkan nilai maksimum.

2. Nilai b

- Jika a dan bbertanda sama atau a . b > 0, maka puncak parabola berada di sebelah kirisumbu y.

- Jika a dan bberbeda tanda atau a . b < 0, maka puncak parabola berada di sebelah kanan sumbuy.

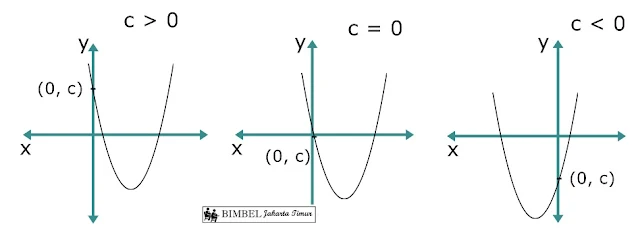
3. Nilai c

- Jika c > 0, parabola memotong sumbu ypositif.

- Jika c=0,maka salah satu akarnya adalah 0 sehingga memotong sumbu y di titik (0,0)

- Jika c < 0, parabola memotong sumbu y negatif.

Titik potongparabola dengan sumbu y didapat ketika nilai x=0. Substitusikan nilaitersebut pada persamaan umum fungsi kuadrat.

contoh : 

Titik potong fungsi y=x² + 3x + 2, x=0

y=0² + 3(0) + 2

y=0

titik potong=(0,2)

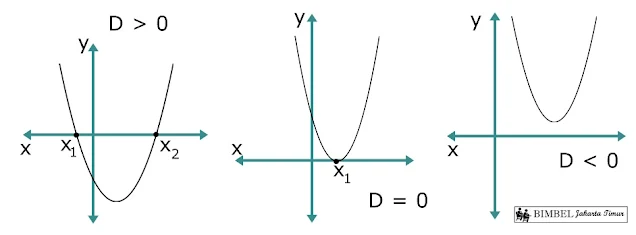
4. NilaiDiskriminan (D=b² – 4ac)

- Jika D > 0,maka parabola memotong sumbu x di dua titik.

- Jika D=0,maka parabola memotong sumbu x di satu titik atau menyinggung sumbu x.

- Jika D < 0,parabola tidak memotong sumbu x

Titik potongparabola dengan sumbu x didapat ketika nilai y=0. Titik potong tersebutadalah akar-akar persamaan yang ditentukan dengan cara memfaktorkan,menggunakan rumus atau kuadrat sempurna.

Baca juga :  Mencari akar-akar persamaan kuadrat

5. Titik ekstrim (titik puncak)

Grafik fungsi kuadrat atau kurva parabola memiliki titik ekstrim atau titik puncak (x, y) dimana nilai x adalah sumbu simetri dan nilai y adalah nilai ektrim.

Sumbu simetri

Parabola yangdibentuk dari fungsi kuadrat merupakan bentuk yang simetris yang dipotong olehsuatu garis menjadi dua bagian yang sama.

Garis sumbusimetri didapat dengan rumus

Nilai ekstrim fungsi kuadrat

Nilai ekstrim suatu fungsi kuadrat adalah nilai maksimum atau nilai minimum. Nilai minimum adalah nilai y di titik puncak parabola yang terbuka ke atas sedangkan nilai maksimum adalah nilai y di titik puncak parabola yang terbuka ke bawah. Lihat gambar di no 1.

Nilai ekstrim didapatkan dengan rumus :

8. Perubahan grafik fungsi kuadrat

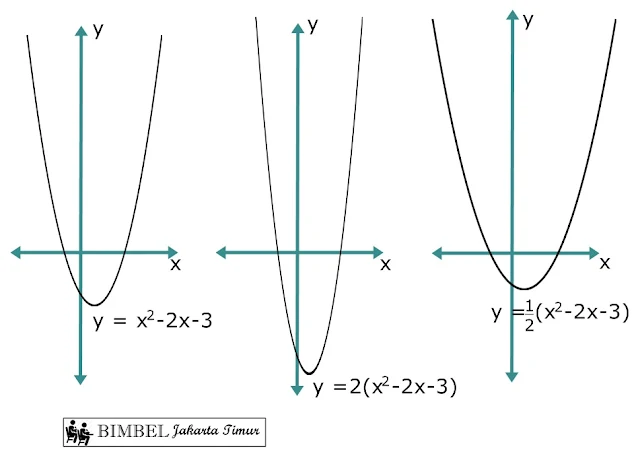
- Jika persamaan fungsi kuadrat dikalikan bilangan lebih kecil dari satu (0 < k < 1), maka kurva parabola yang baru akan lebih lebar dari kurva semula.

- Jika persamaan fungsi kuadrat dikalikan bilangan lebih besar dari satu (k > 1), maka kurva parabola yang baru akan lebih sempit/ramping dari kurva semula.

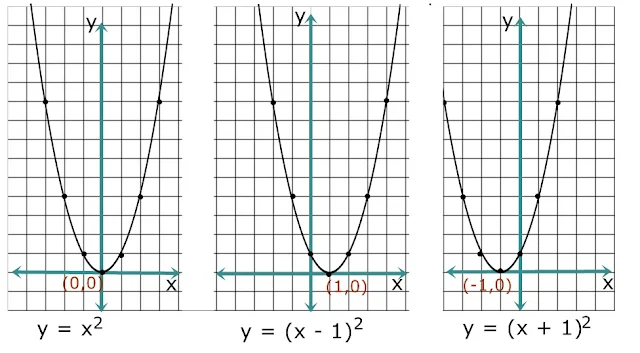
- Jika nilai x berkurang, maka kurva akan bergeser ke kanan dari kurva semula.  Jika nilai x bertambah, maka kurva akan bergeser ke kiri dari kurva semula. 

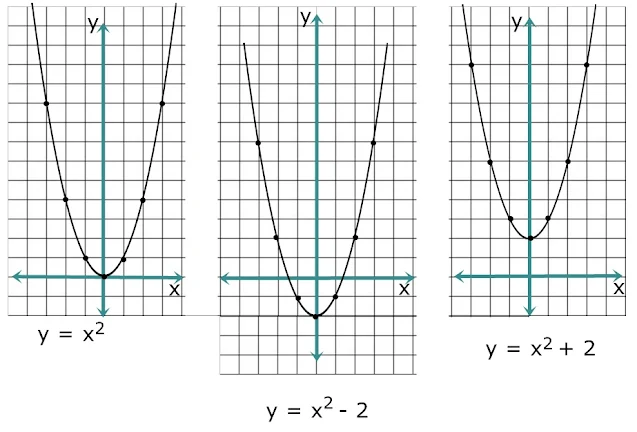
- Jika nilai y berkurang, maka kurva akan bergeser ke bawah. Jika nilai y bertambah, maka kurva akan bergeser ke atas dari kurva semula. 

Menentukan persamaan fungsi kuadrat

1. Jika diketahui tiga titik pada grafik/kurva

Substitusi nilai x dan y dari masing-masing titik ke persamaan umum fungsi, lalu eliminasi untuk mendapatkan nilai koefisien dan konstantanya.

contoh : 

Persamaan fungsi kuadrat yang melalui titik (-3, 9), (0, -6) dan (2, 4)

cara :

➤titik pertama (-3, 9), maka x=-3 dan y=9

Persamaan umum : y=ax² + bx + c

9=a(-3)² + b(-3) + c

9=9a - 3b + c ....... (I)

➤titik kedua (0, -6), maka x=0 dan y=-6

Persamaan umum : y=ax² + bx + c

-6= a(0)² + b(0) + c

-6=c

substitusi nilai c ke persamaan (I)

9=9a - 3b + c

9=9a - 3b - 6

9 + 6=9a - 3b

15=9a - 3b (sederhanakan dengan membagi 3)

3a - b=5.... (II)

➤ titik ketiga (2,4) maka x=2 dan y=4

Persamaan umum : y=ax² + bx + c

4=a(2)² + b(2) - 6

4 + 6=4a + 2b 

10=4a + 2b (sederhanakan dengan membagi 2)

2a + b=5....(III)

eliminasi (II) dan (III)

3a - b=5

2a + b=5  +

5a=10

a=2

2a + b=5

2(2) + b=5

b=5 - 4=1

nilai a=2, b=1 dan c=-6

Persamaan y=ax² + bx + c

y=2x² + x - 6

2. Jika diketahui titik potong sumbu x dan satu titik lain pada kurva.

Titik potong sumbu x adalah (x1, 0) dan (x2, 0), satu titik lain pada kurva adalah (x,y). Substitusi nilai-nilai berikut ke dalam rumus untuk mendapatkan nilai a.

Sebuah kurva memotong sumbu x di titik (3, 0) dan (5, 0) serta melalui titik (2, -3). Persamaan kurva tersebut adalah...

cara :

x1=3, x2=5 dan (x, y)=(2, -3)

Rumus : y=a (x - x1) (x - x2)

-3=a (2 - 3) (2 - 5)

-3=a (-1) (-3)

-3=3a

a=-1

substitusi kembali nilai a, x1 dan x2 ke dalam rumus

y= a (x - x1) (x - x2)

y=-1(x - 3) (x - 5)

y=-1(x² - 8x + 15)

y= -x² + 8x - 15

3. Jika diketahui titik puncak dan satu titik lain pada kurva

Titik puncak (xp, yp) dan satu titik lain pada kurva adalah (x,y). Substitusi nilai-nilai berikut ke dalam rumus untuk mendapatkan nilai a.

contoh :

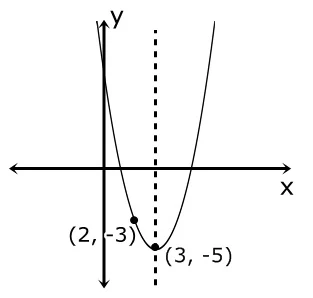
Tentukan persamaan dari fungsi berikut 

(xp, yp)=(3, -5) dan (x, y)=(2, -3)

Rumus : y - yp=a(x - xp)²

-3 - (-5)=a(2 - 3)²

2=a (-1)²

a=2

substitusi kembali nilai a, xp dan yp ke dalam rumus

y - (-5)=2(x - 3)²

y + 5=2(x² - 6x + 9)

y + 5= 2x² - 12x + 18

y= 2x² - 12x + 18 - 5

y= 2x² - 12x + 13

Demikian ringkasan materi tentang grafik fungsi kuadrat yang dapat kami berikan. Untuk dapat melatih kemampuanmu, kamu dapat mencoba soal-soal berikut : Soal Fungsi Kuadrat Kelas 9

https://www.radarhot.com/2020/10/grafik-fungsi-kuadrat.html