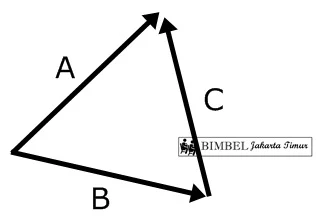
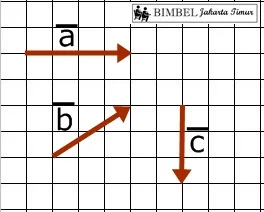
1. Tiga buah vektor A, B dan C memiliki arah dan besar seperti gambar berikut.
Pernyataan yang benar adalah....
a. A + B + C=0
b. A + B=C
c. B + C=A
d. A + C=B
Pembahasan :
Vektor A bertitik asal sama dengan vektor B dan berakhir di titik akhir vektor C, maka A=B + C atau
B + C=A
Jawaban : c
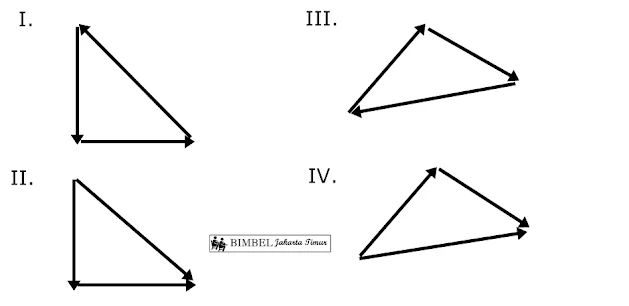
2. Perhatikan gambar penjumlahan vektor berikut.
Resultan vektor sama dengan 0 ditunjukkan oleh gambar...
a. I dan III
b. II dan IV
c. I, II, dan III
d. IV saja
Pembahasan :
Resultan vektor sama dengan 0 jika tidak ada tanda panah yang bertumbukan atau setiap titik asal vektor yang satu akan menyambung titik akhir (panah) vektor yang lain.
I. tidak ada tanda panah yang bertumbukan (resultan=0)
II. ada tanda panah yang bertumbukan (resultan ≠ 0)
III. tidak ada tanda panah yang bertumbukan (resultan=0)
IV. ada tanda panah yang bertumbukan (resultan ≠ 0)
Jawaban : a
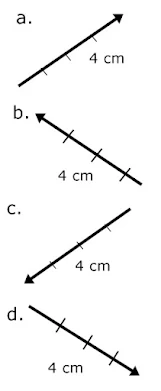
3. Sebuah vektor ā digambarkan seperti berikut
Maka vektor -2ā digambarkan sebagai....
Pembahasan :
Jika a panjangnya 2 cm, maka 2a panjangnya 2 x 2 cm=4 cm. Tanda negatif menunjukkan arah yang berlawanan. Jika a arahnya ke kanan atas, maka -2a arahnya ke kiri bawah.
Jawaban : c
4. Dua buah vektor F1 dan F2 masing- masing besarnya 5 N dan 8 N. Besar resultan kedua vektor yang tidak mungkin adalah...
a. 3 N
b. 5 N
c. 12 N
d. 15 N
Pembahasan :
Nilai resultan terkecil didapat jika kedua vektor sejajar dan berlawanan arah. Besarnya adalah selisih kedua vektor tersebut
8 - 5=3N
Nilai resultan terbesar didapat jika kedua vektor sejajar dan searah. Besarnya adalah penjumlahan kedua vektor tersebut
5 + 8=13 N
Nilai resultan yang tidak mungkin adalah yang nilainya lebih kecil dari selisih ataupun lebih besar dari jumlah vektor.
Jawaban : d
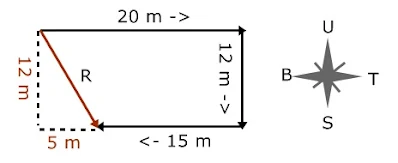
5. Sebuah mobil bergerak ke arah Timur sejauh 20 m lalu berbelok ke Selatan sejauh 12 m. Mobil itu kemudian berbelok kembali ke arah Barat sejauh 15 m. Besar perpindahan yang dilakukan mobil tersebut adalah....
a. 13 m
b. 25 m
c. 35 m
d. 47 m
Pembahasan :
Perhatikan gambar berikut !
Berdasarkan arah mata angin maka mobil itu bergerak ke Timur (kanan) 20 m, Selatan (bawah) 12 m dan ke Barat (kiri) 15 m. Dari gambar terlihat bahwa total pergerakan mobil ke arah vertiksl 12 m dan horisontal (20-15) m. Maka perpindahan mobil dapat kita hitung menggunakan phitagoras.
R²=12² + 5²
=144 + 25
=169
R=√169=13 m
Jawaban : a
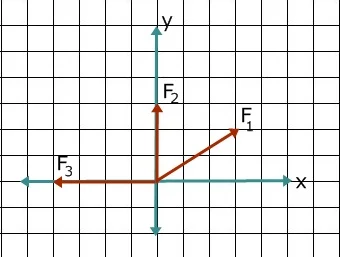
6. Tiga buah vektor digambarkan dalam diagram berpetak berikut. Setiap vektor dapat dinyatakan dalam bentuk koordinat (x,y).
Koordinat yang mewakili
a. (10,4)
b. (10,1)
c. (7,-1)
d. (7,1)
Pembahasan :
koordinat a=(4,0)
koordinat b=(3,2)
koordinat c=(0,-3)
R=a + 2b + c
Rx=4 + 2(3) + 0=10
Ry=0 + 2(2) - 3=1
koordinat R=(10,1)
Jawaban : b
7. Dari gambar nomer 6, besar
a. -5√2 satuan
b. -5 satuan
c. 5 satuan
d. 5√2 satuan
Pembahasan :
Rx=2(4) - 3 + 0=5
Ry=2(0) - 2 - 5=5
R²=Rx² + Ry²
=5² + (-5)²
=50
R=√50
=5√2 satuan
Jawaban : d
8. Dua buah vektor F1 dan F2 masing- masing besarnya 15 N dan 8 N. Jika resultan kedua vektor tersebut adalah 17 N, maka besar sudut yang diapit vektor F1 dan F2 adalah....
a. 30°
b. 45°
c. 60°
d. 90°
Pembahasan :
F² = F1² + F2² + 2.F1.F2. cos θ
17²=15² + 8² + 2.15.18.cos θ
289=225 + 64 + 540.cos θ
289 - 225 - 64= 540.cos θ
0 = 540.cos θ
cos θ=0
θ= 90°
Jawaban : d
9. Dua buah vektor F1 dan F2 masing- masing besarnya 6 N dan 8 N. Jika besar sudut yang diapit kedua vektor tersebut adalah 60°, maka besar |F1+F2| adalah...
a. √128 N
b. √148 N
c. √156 N
d. √196 N
Pembahasan :
|F1+F2|²= F1² + F2² + 2.F1.F2. . cos 𝛉
=6² + 8² + 2.6.8.cos 60°
=36 + 64 + 96. 0,5
=148
|F1+F2|=√148 N
Jawaban : b
10. Vektor A besarnya 7 N dan vektor B besarnya 5 N. Kedua vektor membentuk sudut 60°. Resultan selisih kedua vektor adalah....
a. 4 N
b. √39 N
c. √74 N
d. 9 N
Pembahasan :
|F1-F2|²= F1² + F2² - 2.F1.F2. cos 𝛉
=7² + 5² - 2. 7. 5. cos 60°
=49 + 25 - 35
=39
|F1-F2|=√39 N
Jawaban : b
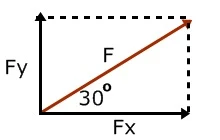
11. Jika sebuah vektor 18 N diuraikan menjadi dua buah vektor yang saling tegak lurus dan yang sebuah dari padanya membentuk sudut 30° dengan vektor itu, maka besar masing- masing vektor adalah...
a. 3 N dan 6 N
b. 9 N dan 9√2 N
c. 9 N dan 9√3 N
d. 9√3 N dan 18 N
Pembahasan :
Kita misalkan vektor yang akan diuraikan adalah F yang akan diuraikan menjadi dua vektor yang saling tegak lurus yaitu Fx dan Fy. Vektor Fx adalah vektor yang membentuk sudut 30° dengan vektor F seperti gambar berikut.
Fx=F. cos 30°
=18 . ½√3
=9√3 N
Fy=F. sin 30°
=18 . ½
=9 N
Jawaban : c
12. Sebuah vektor mempunyai komponen pada sumbu x, yaitu Fx=12 N. Vektor tersebut membentuk sudut 53° terhadap sumbu x positif. Besar komponen y vektor itu atau Fy adalah....
a. 8 N
b. 10 N
c. 15 N
d. 16 N
Pembahasan :
Fx=F. cos 53°
12=F. 0,6
F =12 : 0,6=20 N
Fy=F. sin 53°
=20. 0,8
=16 N
Jawaban : d
13. Dua buah vektor masing -masing besarnya 12 N dan 16 N saling tegak lurus. Arah resultan terhadap vektor 16 N adalah....
a. 30°
b. 37°
c. 53°
d. 60°
Pembahasan :
Diketahui : V1=12 N dan V2=16 N, θ=90°
Ditanya : sudut terhadap V2, kita misalkan β
Besar resultan kedua vektor (V)
V²=V1² + V2² + 2.V1.V2.cos 90°
=12² + 16² + 2.12.16.0
=144 + 256 + 0
=400
V=√400=20 N
mencari sudut β menggunakan rumus
V = V1
sin θ sin β
20 = 12
1 sin β
sin β= 12 x 1
20
=0,6
β= 37°
Jawaban : b
14. Dua buah vektor yang besarnya sama mengapit sudut β. Jika resultan jumlah kedua vektor besarnya dua kali resultan selisih, maka besar sudut β adalah....
a. 30°
b. 37°
c. 53°
d. 60°
Pembahasan :
Kedua vektor sama besarnya, kita misalkan A.
Sudut yang diapit adalah β, serta
|A + A| =2 |A - A|, maka
|A + A|²=4 |A - A|²
A² + A² + 2.A.A. cos β=4 (A² + A² - 2.A.A. cos β)
2A² + 2A². cos β =8A² - 8A². cos β
2A². cos β+ 8A². cos β = 8A² - 2A²
10A². cos β =6A²
cos β = 6A² : 10A²=0,6
β =53°
Jawaban : c
15. Tiga buah vektor digambarkan seperti gambar berikut dengan 1 skala=1 satuan.
Besar resultan ketiga vektor adalah...
a. √26 satuan
b. √27 satuan
c. √29 satuan
d. √30 satuan
Pembahasan :
F1x=3, F1y=2
F2x=0, F2y=3
F3x=-4, F3y=0
Fx=3 + 0 -4=-1
Fy=2 + 3 + 0=5
F²=Fx² + Fy²
=(-1)² + 5²
=1 + 25
=26
F=√26 satuan
Jawaban : a
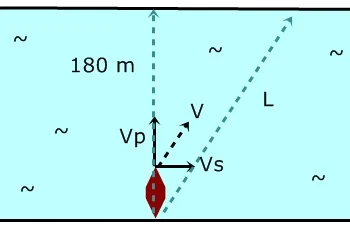
16. Sebuah perahu menyeberangi sungaiyang lebarnya 180 m dan kecepatan arus air 5 m/s. Bila perahu diarahkan menyeberang tegak lurus dengan kecepatan 12 m/s, tentukan panjang lintasan yang ditempuhperahu hingga sampai ke seberang sungai!
a. 75 m
b. 195 m
c. 240 m
d. 432 m
Pembahasan :
Perhatikan gambar berikut
Jika Vp adalah vektor kecepatan perahu dan Vs adalah vektor kecepatan arus sungai, maka V adalah resultan kedua vektor tersebut dengan sudut apit 90°.
V²=Vp² + Vs²
=12² + 5²
=144 + 25
=169
V=13 m/s
Karena lebar sungai sejajar dengan vektor kecepatan perahu dan panjang lintasan L sejajar dengan vektor kecepatan V, maka berlaku perbandingan
L = V
180 Vs
L= V x 180
Vs
= 13 x 180
12
=195 m
Jawaban : b
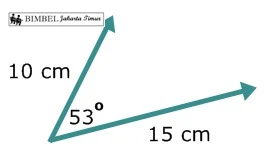
17. Dua buah vektor seperti gambar berikut
Besar resultan kedua vektor adalah....
a. √85 cm
b. √145 cm
c. √325 cm
d. √505 cm
Pembahasan :
|F1+F2|²= F1² + F2² + 2.F1.F2. cos 𝛉
=10² + 15² + 2.10.15. cos 53°
=100 + 225 + 2.10.15. 0,6
=325 + 180
=505
|F1+F2|= √505 cm
Jawaban : d
18. Dua buah vektor gaya masing-masing 8 N dan 5 N saling mengapit sudut 120°. Besar resultan kedua vektor tersebut adalah....
a. 6 N
b. 7 N
c. 9 N
d. 11 N
Pembahasan :
|F1+F2|²= F1² + F2² + 2.F1.F2. cos 𝛉
=8² + 5² + 2.8.5. cos 120°
=64 + 25 + 80. (-0,5)
=89 - 40
=49
|F1+F2|= √49=7 N
Jawaban : b
19. Dua buah vektor yang sama besar yaitu 9 N saling mengapit sudut 60°. Besar sudut yang dibentuk resultan kedua vektor dengan vektor pertama adalah....
a. 30°
b. 37°
c. 45°
d. 53°
Pembahasan :
R²=9² + 9² + 2.9.9. cos 60°
=81 + 81 + 2.81.0,5
=243
R= √243=9√3 N
Jika sudut yang dibentuk oleh resultan dan vektor pertama adalah β, maka
R = F2
sin θ sin β
9√3 = 9
½√3 sin β
sin β= 9 x ½√3
9√3
=0,5
β= 30°
Jawaban : a
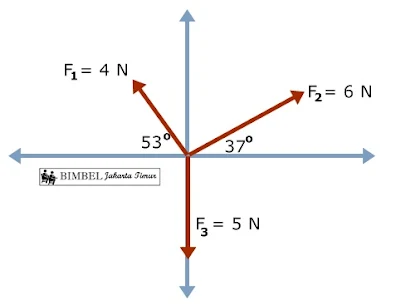
20. Diberikan tiga buah vektor seperti gambar berikut
Besar resultan ketiga vektor tersebut adalah....
a. √3 N
b. 3 N
c. 4 N
d. 5 N
Pembahasan :
Uraikan ketiga vektor berdasarkan komponen sumbu x dan sumbu y
F1x=F1. (-cos 53°)=4 . (-0,6)=-2,4 N
F1y=F1. sin 53°=4. 0,8=3,2 N
F2x=F2 . cos 37°=6 . 0,8=4,8 N
F2y=F2 . sin 37°=6. 0,5=3,6 N
F3x=0
F3y=- 5 N
Fx=-2,4 + 4,8 + 0=2,4 N
Fy=3,2 + 3,6 - 5=1,8 N
F²=Fx² + Fy²
=2,4² + 1,8²
=5,76 + 3,24
=9
F= √9=3 N
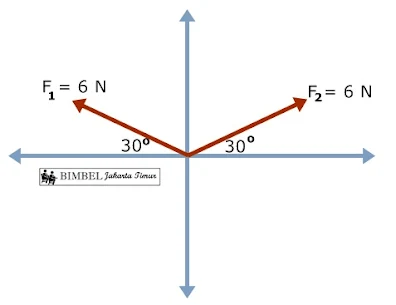
21. Dua buah vektor digambarkan pada sumbu koordinat seperti gambar berikut
Gaya ketiga yang membuat keseimbangan dengan gaya-gaya F1 dan F2 adalah....
a. 3 N dengan sudut 30° terhadap sumbu x negatif
b. 3 N searah sumbu y positif
c. 6 N searah sumbu y positif
d. 6 N searah sumbu y negatif
Pembahasan :
F1x=F1. (-cos 30°)=6 . (-½√3)=-3√3 N
F1y=F1. sin 30°=6. 0,5=3 N
F2x=F2 . cos 30°=6 . ½√3 = 3√3 N
F2y=F2 . sin 30°=6. 0,5=3 N
Fx= -3√3 + 3√3=0
Fy=3 + 3=6 N
Karena besar resultan kedua vektor adalah 6 N searah sumbu y negatif, maka agar gaya-gayanya seimbang harus diberi gaya ke tiga yang sama besar dan berlawanan arah yaitu 6 N searah sumbu y negatif.
Jawaban : d
22. Diketahui dua buah vektor yaitu vektor A=3i - 2j + 5k dan vektor B=5i + 11j + 7k. Resultan kedua vektor tersebut adalah...
a. 15 satuan
b. 17 satuan
c. 19 satuan
d. 21 satuan
Pembahasan :
A + B=(3 + 5)i + (-2 + 11)j + (5 + 7)k
=8i + 9j + 12k
|A + B|²=8² + 9² + 12²
=64 + 81 + 144
=289
|A + B|=√289=17 satuan
Jawaban : b
23. Diketahui dua buah vektor yaitu vektor p=i - j + 2k dan vektor q=i + k. Besar sudut yang diapit kedua vektor adalah....
a. 30°
b. 37°
c. 53°
d. 60°
Pembahasan :
p=(1,-1,2), q=(1, 0, 1)
p . q= (1x1) + (-1 x 0) + (2x1)
=1 + 0 + 2
=3
|p|=√(1² + (-1)² + 2²)
=√6
|q|= √(1² + 0² + 1²)
=√2
p . q=|p|.|q|.cos θ
3 = √6.√2. cos θ
3 =2√3 . cos θ
cos θ= 3
2√3
= ½√3
θ=30°
Jawaban : a
24. Dua buah vektor a dan b saling tegak lurus. Jika a=3i + j - 2k dan b=-i + pj + 2k, maka nilai |b| adalah....
a. 3 satuan
b. 3√3 satuan
c. 3√6 satuan
d. 6 satuan
Pembahasan :
a . b=|a|.|b|.cos θ
(3 x -1) + (1 x p) + (-2 x 2)= |a|.|b|.cos 90°
-3 + p -4= |a|.|b|. 0
p - 7=0
p=7
b=-i + 7j + 2k
|b|²=(-1)² + 7² + 2²
=1 + 49 + 4
=54
|b|=√54
=3√6 satuan
Jawaban : c
25. Diketahui dua buah vektor m dan n. Jika m=2i - 2j + 4k dan n=3i + j - 5k, maka hasil perkalian titik dan perkalian silang kedua vektor adalah...
a. -4 dan -6i - 2j - 8k
b. 4 dan -6i - 22j - 8k
c. 16 dan -6i - 2j - 8k
d. 16 dan -6i - 22j - 8k
Pembahasan :
m=2i - 2j + 4k
n=3i + j - 5k
Perkalian titik
m . n=(2x3) + (-2x1) + (4x-5)
=6 -2 -20
=-16
Perkalian silang
m x n=(-6k + 4i - 10j) - (10i + 12j + 2k)
=-6i - 22j - 8k
Jawaban : d
Baca juga : Soal GLB dan GLBB Kelas 10






%20By%20Bimbel%20Jakarta%20Timur.webp)



