Soal Sistem Persamaan Linear Kuadrat (SPLK) dan Sistem Persamaan Kuadrat Kuadrat (SPKK)
1. Sistem persamaan x - y=3 dan x² + y² + 2x - 6y - 15=0 mempunyai .... penyelesaian
a. 0
b. 1
c. 2
d. 3
Pembahasan :
x - y=3
- y=3 - x
y=x - 3
Substitusi persamaan linear ke persamaan kuadrat
x² + y² + 2x - 6y - 15=0
x² + (x-3)² + 2x - 6(x-3) - 15=0
x² + x² - 6x + 9 + 2x - 6x + 18 - 15=0
2x² - 10x + 12=0
a=2, b=-10, c=12
maka nilai diskriminan adalah
D=b² - 4ac
=(-10)² - 4.2.12
=100 - 96
=4
D > 0, garis dan kurva saling berpotongan di dua titik maka memiliki 2 penyelesaian.
Jawaban : c
2. Kedudukan garis y=x - 4 dan kurva y= x² - 7x + 12 adalah....
a. tidak saling berpotongan
b. bersinggungan di satu titik
c. berpotongan di dua titik
d. tidak dapat digambarkan
Pembahasan :
Substitusi garis y=x - 4 ke persamaan kurva y= x² - 7x + 12
y = x² - 7x + 12
x - 4 = x² - 7x + 12
0 = x² - 8x + 16
Tentukan nilai diskriminan
a=1, b=-8, c=16
D= b² - 4ac
=(-8)² - 4.1.16
=64 - 64
=0
D=0, garis dan kurva saling bersinggungan di satu titik
Jawaban : b
3. Kedudukan garis y=2x - 1 dan kurva x² + y² + 2xy - x - y + 4=0 adalah....
a. tidak saling berpotongan
b. bersinggungan di satu titik
c. berpotongan di dua titik
d. tidak dapat digambarkan
Pembahasan :
Substitusi garis y=2x - 1 dan kurva x² + y² + 2xy - x - y + 4=0
x² + y² + 2xy - x - y + 4=0
x² + (2x-1)² + 2x(2x-1) - x - (2x-1) + 4=0
x² + 4x² - 4x + 1 + 4x² - 2x - x - 2x + 1 + 4=0
9x² - 9x + 6=0
Tentukan nilai diskriminan
a=9, b=-9, c=6
D= b² - 4ac
=(-9)² - 4.9.6
=81 - 216
=- 135
D < 0, garis dan kurva tidak mempunyai penyelesaian karena tidak berpotongan
Jawaban : a
4. Absis perpotongan garis x - y=3 dengan kurva x² + y² + 4xy + 3=0 adalah...
a. 0 dan -2
b. -1 dan 1
c. 1 dan 2
d. 1 dan 3
Pembahasan :
x - y=3 ⇒ y=x - 3
x² + y² + 4xy + 3=0
x² + (x-3)² + 4x(x-3) + 3=0
x² + x² - 6x + 9 + 4x² - 12x + 3=0
6x² - 18x + 12=0 (sederhanakan)
x² - 3x + 2=0 (faktorkan)
(x - 1) (x - 2)=0
x=1 dan x=2
Jawaban : c
5. Garis y + x=0 dan kurva y=2x² - 11x + 12 memiliki dua titik potong di x1 dan x2. Nilai x1 + x2 adalah....
a. - 6
b. -5
c. 1
d. 5
Pembahasan :
y + x=0 ⇒ y=-x
y=2x² - 11x + 12
-x =2x² - 11x + 12
0= 2x² - 10x + 12 (sederhanakan)
0= x² - 5x + 6 (faktorkan)
0=(x-2) (x-3)
x1=2 dan x2=3
x1 + x2=2 + 3=5
Jawaban : d
6. Himpunan penyelesaian dari sistem persamaan
adalah....a. {(2,0) dan (4,2)}
b. {(2,0) dan (5,3)}
c. {(0,-2) dan (5,3)}
d. {(0,-2) dan (4,2)}
Pembahasan :
y=x - 2
(x-2)² + (y-3)²=9
(x-2)² + (x-2-3)²=9
(x-2)² + (x-5)²=9
x² - 4x + 4 + x² - 10x + 25 - 9=0
2x² - 14x + 20=0 (sederhanakan)
x² - 7x + 10=0 (faktorkan)
(x-2) (x-5)=0
x1=2 dan x2=5
y=x - 2, maka
y1=x1 - 2=2 - 2=0
(2,0)
y2=x2 - 2=5 - 2=3
(5,3)
Hp={(2,0) dan (5,3)}
Jawaban : b
7. Garis y + 2x=5 memotong kurva x² + 4x + y=8 di dua titik. Jarak kedua titik tersebut adalah....
a. 3 satuan
b. 4 satuan
c. 4√3 satuan
d. 4√5 satuan
Pembahasan :
y + 2x=5 ⇒ y=-2x + 5
x² + 4x + y=8
x² + 4x + (-2x + 5) - 8=0
x² + 2x - 3=0
(x + 3) (x - 1)=0
x=-3 dan x=1
y=-2x + 5, untuk x=-3
y=-2(-3) + 5
=6 + 5=11
(-3,11)
y=-2x + 5, untuk x=1
y=-2(1) + 5
=-2 + 5=3
(1,3)
Rumus jarak dua titik
R²=(x1 - x2)² + (y1 - y2)²
=(-3 - 1)² + (11 - 3)²
=16 + 64
=80
R=√80
=4√5 satuan
Jawaban : d
8. Garis y + x=8 memotong kurva x² + y² -4(x+y)=8 di dua titik. Jarak kedua titik tersebut adalah....
a. 2 satuan
b. 2√2 satuan
c. 4√2 satuan
d. 6√2 satuan
Pembahasan :
y + x=8 ⇒ y=8 - x
x² + y² -4(x+y)=8
x² + (8 - x)² -4(8) - 8=0
x² + 64 - 16x + x² - 32 - 8=0
2x² - 16x + 24=0 (sederhanakan)
x² - 8x + 12=0 (faktorkan)
(x - 2) (x - 6)=0
x=2 dan x=6
y=8 - x untuk x=2
y=8 - 2=6
(2,6)
y=8 - x untuk x=6
y=8 - 6=2
(6,2)
R²=(x1 - x2)² + (y1 - y2)²
=(2 - 6)² + (6 - 2)²
=16 + 16
=32
R=√32
=4√2 satuan
Jawaban : c
9. Garis y + 2x + a=0 menyinggung kurva y= x² + 6x + 5 di satu titik. Nilai a yang memenuhi adalah....
a. 3
b. 4
c. 9
d. 11
Pembahasan :
y + 2x + a=0 ⇒ y=- 2x - a
y= x² + 6x + 5
- 2x - a= x² + 6x + 5
0= x² + 6x + 5 + 2x + a
0= x² + 8x + 5 + a
Bersinggungan, maka D=0
a=1, b=8, c=5 + a
D= b² - 4ac
0=8² - 4.1.(5 + a)
0=64 - 20 - 4a
4a=44
a=11
Jawaban : d
10. Himpunan penyelesaian dari sistem persamaan
adalah....
a. {(0,12) dan (6,0)}
b. {(0,6) dan (12,0)}
c. {(0,12) dan (-6,0)}
d. {(0,-6) dan (12,0)}
Pembahasan :
y + 2x=12 ⇒ y=-2x + 12
y=-x² + 4x + 12
-2x + 12= -x² + 4x + 12
-2x + 12 + x² - 4x - 12=0
x² - 6x=0
x(x - 6)=0
x=0 dan x=6
y=-2x + 12 untuk x=0
y=-2(0) + 12=12
(0,12)
y=-2x + 12 untuk x=6
y=-2(6) + 12=0
(6,0)
Hp={(0,12) dan (6,0)}
Jawaban : a
11. Titik potong garis y=3x - 3 dengan kurva y= x² + 2x - 15 adalah...
a. (3,-9)
b. (-4,9)
c. (-3,-9) dan (4,9)
d. (3,-9) dan (-4,9)
Pembahasan :
y=3x - 3
y= x² + 2x - 15
Titik potong garis dan kurva
y= x² + 2x - 15
3x - 3= x² + 2x - 15
0= x² + 2x - 15 - 3x + 3
0= x² - x - 12
0=(x+3) (x-4)
x=-3 dan x=4
y=3x - 3 untuk x=-3
y=3(-3) - 3=-9
(-3,-9)
y=3x - 3
y=3(4) - 3=9
(4,9)
Jawaban : c
12. Hubungan kurva y= x² - 12x + 35 dan y=-x² + 8x - 15 adalah....
a. tidak saling berpotongan
b. bersinggungan di satu titik
c. berpotongan di dua titik
d. tidak dapat digambarkan
Pembahasan :
y= x² - 12x + 35 dan y=-x² + 8x - 15
x² - 12x + 35=-x² + 8x - 15
x² - 12x + 35 + x² - 8x + 15=0
2x² - 20x + 50=0
a=2, b=-20, c=50
D=b² - 4ac
=(-20)² - 4.2.50
=400 - 400
=0
D=0, bersinggungan di satu titik
Jawaban : b
13. Kurva parabola y= 2x² + 3x - 5 dan y= x² + x - 6 berpotongan di titik....
a. (0,-6)
b. (0,-5)
c. (-1,-6)
c. (-1,5)
Pembahasan :
y= 2x² + 3x - 5 dan y= x² + x - 6, maka
2x² + 3x - 5= x² + x - 6
2x² + 3x - 5 - x² - x + 6=0
x² + 2x + 1=0
(x+1) (x+1)=0
x=-1 (hanya 1 titik)
y= x² + x - 6
=(-1)² + (-1) - 6
=-6
titiknya (-1,-6)
Jawaban : c
14. Himpunan penyelesaian dari sistem persamaan y= x² + 2 dan x² + y²=4 adalah....
a.{(0,-3) dan (0,2)}
b.{(0,-3)}
c.{(0,-2)}
d.{(0,2)}
Pembahasan :
y= x² + 2
⇒ y - 2= x²
⇒ x² + y²=4
y - 2 + y²=4
y² + y - 6=0
(y+3) (y-2)=0
y=-3 dan y=2
⇒ y - 2= x² untuk y=-3
-3 - 2= x²
-5 = x² (tidak ada penyelesaian)
⇒ y - 2= x² untuk y=2
2 - 2= x²
0= x²
x=0
(0,2)
Jawaban : d
15. Kurva y=2x² - 20 dan y= x² + 2x - 12 berpotongan di dua titik. Jarak kedua titik tersebut adalah....
a. 9 satuan
b. 9√11 satuan
c. 9√17 satuan
d. 11 satuan
Pembahasan :
y=2x² - 20 dan y= x² + 2x - 12
2x² - 20 = x² + 2x - 12
2x² - 20 - x² - 2x + 12=0
x² - 2x - 8=0
(x+2)(x-4)=0
x=-2 dan x=4
y=2x² - 20 untuk x=-2
y=2(-2)² - 20=-12
(-2,-12)
y=2x² - 20 untuk x=4
y=2(4)² - 20=12
(4,12)
R²=(x1 - x2)² + (y1 - y2)²
=(-2 - 4)² + (-12 - 12)²
=36 + 576
=612
R=√612
=9√17 satuan
Jawaban : c
16. Titik potong kurva y=x² – 1 dan y=x² – 2x – 3 adalah...
a. (0,-1)
b. (0,1)
c. (1,0)
d. (-1,0)
Pembahasan :
y=x² – 1 dan y=x² – 2x – 3
x² – 1 =x² – 2x – 3
x² – x² + 2x = – 3 + 1
2x=-2
x=-1
y=x² – 1
=(-1)² - 1
=0
(-1,0)
Jawaban : d
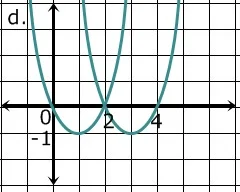
17. Sketsa penyelesaian sistem persamaan y= x² - 2x dan y=-x² + 6x - 8 adalah...
Pembahasan :
y= x² - 2x
Pembuat nol fungsi
x² - 2x=0
x(x-2)=0
x=0 dan x=2
(0,0) dan (2,0)
Puncak grafik
x=-b/2a=2/2=1
y=(1)² - 2(1)=-1
(1,-1)
y=-x² + 6x - 8
Pembuat nol fungsi
-x² + 6x - 8=0
(-x + 2) (x-4)=0
x=2 dan x=4
(2,0) dan (4,0)
Puncak grafik
x=-b/2a=-6/-2=3
y=-(3)² + 6(3) - 8
=-9 + 18 - 8=1
(3,1)
Titik potong y= x² - 2x dan y=-x² + 6x - 8
x² - 2x =-x² + 6x - 8
2x² - 8x + 8=0 (sederhanakan)
x² - 4x + 4=0
(x-2) (x-2)=0
x=2
y= x² - 2x
=2² - 2(2)=0
(2,0)
Jawaban : b
18. Kurva y= 2x² + x - 6 dan y= x² + x - 6 berpotongan di titik....
a. (0,-6)
b. (0,-3)
c. (0,0)
d. (0,2)
Pembahasan :
y= 2x² + x - 6 dan y= x² + x - 6
2x² + x - 6 = x² + x - 6
x²=0
x=0
y= x² + x - 6
y=0² + 0 - 6=-6
(0,-6)
Jawaban : a
19. Diketahui sistem persamaan kuadrat kuadrat
y=3x² + p
y= x² + 12x + 11
Nilai p yang memenuhi agar tepat memiliki satu penyelesaian adalah...
a. 12
b. 24
c. 29
d. 32
Pembahasan :
y=3x² + p
y= x² + 12x + 11
3x² + p = x² + 12x + 11
2x² - 12x + p - 11=0
agar tepat memiliki satu penyelesaian, maka D=0
a=2, b=-12, c=p - 11
D=b² - 4ac
0=(-12)² - 4.2.(p - 11)
0=144 -8p + 88
8p=232
p=29
Jawaban : c
20. Pasangan persamaan kuadrat yang tidak memiliki titik penyelesaian adalah...
a. y= x² + 2x - 3 dan y=-x² + 2x + 3
b. y= x² - 3x - 4 dan y= x² + 3x + 2
c. y=2x² - x - 10 dan y= x² + 7x + 10
d. y= x² + 2x - 3 dan y=-x² + 4x - 4
Pembahasan :
a. y= x² + 2x - 3 dan y=-x² + 2x + 3
x² + 2x - 3 =-x² + 2x + 3
2x² - 6=0
a=2, b=0, c=-6
D= b² - 4ac
=0² - 4.2.(-6)
=48
D > 0, memiliki dua penyelesaian
b. y= x² - 3x - 4 dan y= x² + 3x + 2
x² - 3x - 4 = x² + 3x + 2
- 6x - 6=0
- 6x=6
x=-1
memiliki satu penyelesaian
c. y=2x² - x - 10 dan y= x² + 7x + 10
2x² - x - 10 = x² + 7x + 10
x² - 8x - 20=0
a=1, b=-8, c=-20
D= b² - 4ac
=(-8)² - 4.1.(-20)
=64 + 80
=144
D > 0, memiliki dua penyelesaian
d. y= x² + 2x - 3 dan y=-x² + 4x - 4
x² + 2x - 3 =-x² + 4x - 4
2x² - 2x + 1=0
a=2, b=-2, c=1
D= b² - 4ac
=(-2)² - 4.2.1
=4 - 8
=-4
D < 0, tidak memiliki penyelesaian
Jawaban : d
D= b² - 4ac
=(-2)² - 4.2.1
=4 - 8
=-4
D < 0, tidak memiliki penyelesaian
Jawaban : d
Tidak ada komentar:
Posting Komentar