Penyelesaian pertidaksamaan rasional hampir mirip dengan pertidaksamaan kuadrat yaitu memfaktorkan, menentukan pembuat nol, menentukan interval yang mungkin terbentuk lalu menentukan tanda atau nilai positif negatif tiap interval dan menyesuaikan dengan ketidaksamaan soal. Pada soal dan penyelesaiannya, ada fungsi rasional yang mempunyai syarat atau aturan tertentu. Misalnya penyebut tidak boleh bernilai nol, fungsi yang memuat pembuat nol kuadrat serta fungsi definit. Untuk lebih jelasnya bisa kamu pelajari dalam contoh soal-soal dan pembahasannya berikut.
TENTUKAN HIMPUNAN PENYELESAIAN PERTIDAKSAMAAN-PERTIDAKSAMAAN BERIKUT !
a.{x| x < -5 atau x > 1}
b. {x| x < -1 atau x > 5}
c. {x| -5 < x < 1}
d. {x| -1 < x < 5}
Pembahasan :
Pembuat nol
x + 5=0, x=-5
x - 1=0, x=1
Intervalyang mungkin x < -5 ; -5 < x < 1; x > 1
untuk x <-5, ambil angka uji -6
(-6+5) : (-6 -1)=(-1) : (-7)=1/7
bernilai positif
untuk -5 < x < 1, ambil angka uji 0
(0+5) : (0 -1)=5 : (-1)=-5
bernilai negatif
untuk x > 1, ambil angka uji 2
(2+5) : (2 -1)=7 : 1=7
bernilai positif
Tanda setiap interval berurutan biasanya akan berselang seling (+) (-) (+) atau (-) (+) (-) kecuali ada syarat lain dalam ketidaksamaan.
Untuk soal ini tanda ketidaksamaan < 0, maka penyelesaian pada interval yang hasilnya negatif yaitu -5 < x < 1
Jawaban : c
a.{x| x < 2 atau x > 3}
b. {x| x < 2 atau x > 6}
c. {x| 2 < x < 3}
d. {x| 2 < x < 6}
Pembuat nol
x - 2=0, x=2
2x - 6=0, x=3
Interval yang mungkin x < 2 ; 2 < x < 3; x > 3
untuk x < 2, ambil angka uji 0
(0 - 2) : (2(0) -6)=(-2) : (-6)=1/3
bernilai positif
untuk 2 < x < 3, bernilai negatif
untuk x > 3, bernilai positif
Tanda ketidaksamaan soal > 0, maka penyelesaian pada interval yang hasilnya positif yaitu x < 2 atau x > 3
a. {x| x ≤ -5 atau x > 4}
b. {x| x ≤ -4 atau x > 5}
c. {x| -5 ≤ x < 4}
d. {x| -4 < x ≤ 5}
Pembuat nol
5 - x=0, x=5
x + 4=0, x=-4
Interval yang mungkin x < -4 ; -4 < x ≤ 5; x ≥ 5
Karena x + 4 adalah penyebut dan penyebut tidak boleh bernilai nol maka x ≠ 4 dan tanda pada -4 tetap < atau >
untuk x < -4, ambil angka uji -5
(5 -(-5)) : (-5+4)=10 : -1=-10
bernilai negatif
untuk -4 < x ≤ 5, bernilai positif
untuk x ≥ 5, bernilai negatif
Tanda ketidaksamaan soal ≤ 0, maka penyelesaian pada interval yang hasilnya negatif yaitu x < -4 atau x ≥ 5
Jawaban : b
a. {x| x ≤ -6 atau x > 2}
b. {x| x < 2 atau x ≥ 6}
c. {x| -6 ≤ x < 2}
d. {x| 2 < x ≤ 6}
Pembahasan :
Pembuat nol
-x + 6=0, x=6
x - 2=0, x=2
Interval yang mungkin x < 2 ; 2 < x ≤ 6; x ≥ 6
untuk x < 2 ambil angka uji 0
(-0+6) : (0-2)=6 : -2=-3
bernilai negatif
untuk 2 < x ≤ 6, bernilai positif
untuk x ≥ 6, bernilai negatif
Tanda ketidaksamaan soal ≥ 0, maka penyelesaian pada interval yang hasilnya positif yaitu 2 < x ≤ 6
Jawaban : d
a.{x| x < 7/3 atau x > 5/2}
b. {x| x < 5/2 atau x > 17/3}
c. {x| 7/3 < x < 5/2}
d. {x| 5/2 < x < 17/3}
Kumpulkan di sebelah kiri dan samakan penyebut
Pembuat nol
-3x + 17=0, x=17/3
2x - 5=0, x=5/2
Interval yang mungkin x < 5/2 ; 5/2 < x < 17/3; x > 17/3
untuk x < 5/2, ambil angka uji 0
(-3(0)+17) : (2(0) -5)=17 : (-5)=-17/5
bernilai negatif
untuk 5/2 < x < 17/3
bernilai positif
untuk x > 17/3
bernilai negatif
Tanda ketidaksamaan soal > 0, maka penyelesaian pada interval yang hasilnya positif yaitu 5/2 < x < 17/3
Jawaban : d
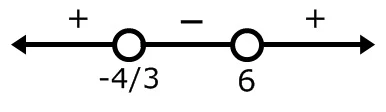
a.{x| x < -4/3}
b. {x| x > -4/3}
c. {x| x < -4/3 atau x > 6}
d. {x| -4/3 < x < 6}
Kumpulkan di sebelah kiri dan samakan penyebut
Pembuat nol
3x + 4=0, x=-4/3
2x - 12=0, x=6
Interval yang mungkin x < -4/3 ; -4/3 < x < 6; x > 6
untuk x < -4/3, ambil angka uji -2
(3(-2)+4) : (2(-2)-12)=(-2) : (-16)=1/8
bernilai positif
untuk -4/3 < x < 6, bernilai negatif
untuk x > 6, bernilai positif
Tanda ketidaksamaan soal > 0, maka penyelesaian pada interval yang hasilnya positif yaitu x < -4/3 atau x > 6
Jawaban : c
a. {x| x ≤ -1 atau x > 2}
b. {x| x < -½ atau x ≥ 1}
c. {x| 1 ≤ x < 2}
d. {x| -½ < x ≤ 1}
Pembahasan :
Kumpulkan di sebelah kiri dan samakan penyebut
Pembuat nol
-2x + 2=0, x=1
2x + 1=0, x=-½
Interval yang mungkin x < -½ ; -½ < x ≤ 1; x ≥ 1
untuk x < -½ , ambil angka uji -1
(-2(-1)+2) : (2(-1)+1)=4 : (-1)=-4
bernilai negatif
untuk -½ < x ≤ 1, bernilai positif
untuk x ≥ 1, bernilai negatif
Tanda ketidaksamaan soal ≥ 0, maka penyelesaian pada interval yang hasilnya positif yaitu -½ < x ≤ 1
Jawaban : d
a.{x| x < -2 atau -1 ≤ x ≤ 5 }
b.{x| x < -2 atau x ≥ 5}
c.{x| -2 < x ≤ -1 atau x ≥ 5}
d.{x| -1 ≤ x ≤ 5}
Pembahasan :
Pembuat nol
x + 1=0, x=-1
x - 5=0, x=5
x + 2=0, x=-2
interval yang mungkin adalah x < -2; -2 < x ≤ -1; -1 ≤ x ≤ 5; x ≥ 5
untuk x < -2, ambil angka uji -3
(-3+1).(-3-5) : (-3+2)
=(-).(-) : (-)=(-) bernilai negatif
untuk -2 < x ≤ -1, bernilai positif
untuk -1 ≤ x ≤ 5, bernilai negatif
untuk x ≥ 5, bernilai positif
Perhatikan bahwa hasilnya selang seling antara positif dan negatif.
Tanda ketidaksamaan soal ≤ 0, maka penyelesaian pada interval yang hasilnya negatif yaitu x < -2 atau -1 ≤ x ≤ 5
Jawaban : a
a. {x| x < -2 atau x ≥ 4}
b. {x| x < -2 atau 3 < x ≤ 4}
c. {x| x ≤ -2 atau 3 ≤ x ≤ 4}
d. {x| -2 < x < 3 atau x > 4}
Pembahasan :
Pembuat nol
x - 4=0, x=4
3 - x=0, x=3
x + 2=0, x=-2
Interval yang mungkin x < -2; -2 < x < 3; 3 < x ≤ 4; x ≥ 4
untuk x < -2, ambil angka uji -3
(-3-4).(3-(-3)) : (-3+2)
=(-).(+) : (-)=(+)
bernilai positif
untuk -2 < x < 3, bernilai negatif
untuk 3 < x ≤ 4, bernilai positif
untuk x ≥ 4, bernilai negatif
Tanda ketidaksamaan soal ≥ 0, maka penyelesaian pada interval yang hasilnya positif yaitu x < -2 atau 3 < x ≤ 4
Jawaban : b
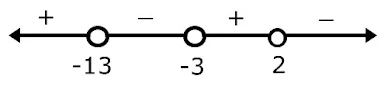
a.{x| x < -13 atau -3 < x < 2}
b. {x| x < -13 atau x > 2}
c. {x| -13 < x < -3 atau x > 2}
d. {x| -13 < x < 2, x ≠ -3}
Pembahasan :
Pembuat nol
-x-13=0, x=-13
x + 3=0, x=-3
x - 2=0, x=2
Interval yang mungkin x < -13; -13 < x < -3; -3 < x < 2; x > 2
untuk x < -13, ambil angka uji -14
(14 - 13) : ((-14 + 3).(-14 - 2))
=(+) : ((-).(-))=(+)
bernilai positif
untuk -13 < x < -3, bernilai negatif
untuk -3 < x < 2, bernilai positif
untuk x > 2, bernilai negatif
Tanda ketidaksamaan soal < 0, maka penyelesaian pada interval yang hasilnya negatif yaitu -13 < x < -3 atau x > 0
Jawaban : c

a.{x| x ≤ -4 atau -2 < x ≤ 0}
b.{x| -4 ≤ x < -2 atau 0 ≤ x < 4}
c.{x| -2 < x ≤ 0 atau x > 4}
d. {x| x ≤ -4 atau -2 < x ≤ 0 atau x > 4}
Pembahasan :
Pembuat nol
x=0
x + 4=0, x=-4
x + 2=0, x=-2
x - 4=0, x=2
Interval yang mungkin x ≤ -4; -4 ≤ x < -2; -2 < x ≤ 0; 0 ≤ x < 4; x > 4
untuk x ≤ -4, ambil angka uji -5
-5(-5+4) : (-5+2).(-5-4)
=-(-) : ((-).(-))=(+)
bernilai positif
untuk -4 ≤ x < -2, bernilai negatif
untuk -2 < x ≤ 0, bernilai positif
untuk 0 ≤ x < 4, bernilai negatif
untuk x > 4, bernilai positif
Tanda ketidaksamaan soal ≤ 0, maka penyelesaian pada interval yang hasilnya negatif yaitu -4 ≤ x < -2 atau 0 ≤ x < 4
Jawaban : b
a.{x| x < -1 atau x > 4}
b. {x| x < -1 atau 3 < x < 4}
c.{x| -1 < x < 4}
d. {x| -3 < x < 4}
Pembahasan :
x² + 3x + 4 adalah definit positif, artinya akan bernilai positif untuk semua x
Definit positif dapat dilihat dengan ciri D < 0 dan a > 0
Selanjutnya cukup faktorkan
x² - 3x - 4=(x + 1) (x - 4)
Pembuat nol
x + 1=0, x=-1
x - 4=0, x=4
Interval yang mungkin x < -1; -1 < x < 4; x > 4
untuk x < -1, ambil angka uji -2
(+) : ((-2+1).(-2-4)
= (+) : ((-).(-))=(+) bernilai positif
maka untuk -1 < x < 4 bernilai negatif
dan untuk x > 4 bernilai positif
Tanda ketidaksamaan soal ≥ 0, maka penyelesaian pada interval yang hasilnya positif yaitu x < -1 atau x > 4
Jawaban : a
a.{x| x < -5 atau x > 4}
b. {x| x < -5 atau x > 5}
c.{x| -5 < x < 4}
d. {x| -5 < x < 5}
Pembahasan :
-x² + 4x - 5 adalah definit negatif, artinya akan bernilai negatif untuk semua x
Definit positif dapat dilihat dengan ciri D < 0 dan a < 0
Selanjutnya cukup faktorkan
x² - 25=(x + 5) (x - 5)
Pembuat nol
x + 5=0, x=-5
x - 5=0, x=5
Interval yang mungkin x < -5; -5 < x < 5; x > 5
untuk x < -5, ambil angka uji -6
(-) : ((-6+5).(-6-5)
= (-) : ((-).(-))=(-) bernilai negatif
maka untuk -5 < x < 5 bernilai positif
dan untuk x > 5 bernilai negatif
Tanda ketidaksamaan soal < 0, maka penyelesaian pada interval yang hasilnya negatif yaitu x < -5 atau x > 5
Jawaban : b
b. {x| x ≤ -2 atau x ≥ 4}
c. {x| -2 ≤ x < 1 atau 1 < x ≤ 4}
d. {x| -2 ≤ x < 1 atau x ≥ 4}
Pembahasan :
Faktorkan
x² - 2x - 8=(x + 2) (x - 4)
x² - 2x + 1=(x - 1)²
Pembuat nol
x + 2=0, x=-2
x - 4=0, x=4
x - 1=0, x=1
Interval yang mungkin x ≤ -2; -2 ≤ x < 1; 1 < x ≤ 4; x ≥ 4
Karena x - 1 berbentuk kuadrat, maka angka 1 terbagi di dua interval dengan tanda yang sama
untuk x ≤ -2, ambil angka uji -3
(-3 + 2) (-3 - 4) : (-3 -1)²
=(-) (-) : (-)²=(+) bernilai positif
maka untuk -2 ≤ x < 1 bernilai negatif
untuk 1 < x ≤ 4 juga bernilai negatif
untuk x ≥ 4 bernilai positif
Tanda ketidaksamaan soal ≤ 0, maka penyelesaian pada interval yang hasilnya negatif yaitu -2 ≤ x < 1 atau 1 < x ≤ 4. Atau dapat juga ditulis -2 ≤ x ≤ 4 dan x ≠ 1 karena 1 bukan penyelesaian.
Jawaban : b
a. {x| x < -3 atau 0 < x < 3}
b. {x| x < -3 atau x > 3}
c. {x| -3 < x < 0 atau x > 3}
d.{x| x < -3 atau 0 < x < 3 atau x > 3}
Pembahasan :
Faktorkan
x² + 3x=x(x + 3)
x² - 6x + 9=(x - 3)²
Pembuat nol
x=0
x + 3=0, x=-3
x - 3=0, x=3
Interval x < -3; -3 < x < 0; 0 < x < 3; x > 3
untuk x < -3, ambil angka uji -4
-4 (-4 + 3) : (-4 - 3)²
=(-) (-) : (-)²=(+) bernilai positif
maka untuk -3 < x < 0 bernilai negatif
untuk 0 < x < 3 bernilai positif
karena (x - 3) berbentuk kuadrat, maka untuk x > 3 juga bernilai positif
Tanda ketidaksamaan soal > 0, maka penyelesaian pada interval yang hasilnya positif yaitu x < -3 atau 0 < x < 3 atau x > 3
Jawaban : d
a.{x| x ≤ -6 atau -3 < x ≤ 1}
b. {x| -6 ≤ x < -3 atau 1 ≤ x < 3}
c. {x| -3 < x ≤ 1 atau x > 3}
d. {x| x ≤ -6 atau -3 < x ≤ 1 atau x > 3}
Pembahasan :
Samakan penyebut dan faktorkan
Pembuat nol
x + 6=0, x=-6
x - 1=0, x=1
x + 3=0, x=-3
x - 3=0, x=3
Interval x ≤ -6; -6 ≤ x < -3; -3 < x ≤ 1; 1 ≤ x < 3; x > 3
untuk x ≤ -6, ambil angka uji -7
(-7 + 6) (-7 - 1) : [(-7 + 3) (-7 - 3)]
=(-) (-) : [(-) (-)]=(+) bernilai positif
untuk -6 ≤ x < -3 bernilai negatif
untuk -3 < x ≤ 1 bernilai positif
untuk 1 ≤ x < 3 bernilai negatif
untuk x > 3 bernilai positif
Tanda ketidaksamaan soal ≤ 0, maka penyelesaian pada interval yang hasilnya negatif yaitu -6 ≤ x < -3 atau -6 ≤ x < -3
Jawaban : b
a.{x| -1 < x < 2}
b.{x| 2 < x < 6}
c.{x| x < -1 atau x > 3}
d. {x| -1 < x < 3}
Pembahasan :
Kumpulkan di satu ruas (kiri) lalu samakan penyebut
Pembuat nol
x - 3=0, x=3
x + 1=0, x=-1
Interval x < -1; -1 < x < 3; x > 3
Pembilang adalah konstanta bernilai negatif
untuk x < -1, ambil angka uji -2
-12 : [(-2 - 3) (-2 + 1)]
=(-) : [(-) (-)]=(-) bernilai negatif
untuk -1 < x < 3 bernilai positif
untuk x > 3 bernilai negatif
Tanda ketidaksamaan soal ≥ 0, maka penyelesaian pada interval yang hasilnya positif yaitu -1 < x < 3
Jawaban : d
a.{x| x < -1 atau -½ ≤ x < 0 atau x ≥ 5}
b.{x| x < -1 atau -½ ≤ x < 0 atau 0 < x ≤ 5}
c. {x| -1 < x ≤ -½ atau 0 < x ≤ 5}
d.{x| -½ ≤ x < 0 atau x ≥ 5}
Pembahasan :
Faktorkan
2x² - 9x - 5= (2x + 1) (x - 5)
x³ + x²= x²(x + 1)
Pembuat nol
2x + 1=0, x=-½
x - 5=0, x=5
x²=0, x=0
x + 1=0, x=-1
Interval x < -1; -1 < x ≤ -½; -½ ≤ x < 0; 0 < x ≤ 5; x ≥ 5
untuk x < -1, ambil angka uji -2
(2(-2)+1) (-2-5) : [(-2)²(-2+1)]
=(-) (-) : [(+)(-)]=(-) bernilai negatif
untuk -1 < x ≤ -½ bernilai positif
untuk -½ ≤ x < 0 bernilai negatif
untuk 0 < x ≤ 5 juga bernilai negatif
untuk x ≥ 5 bernilai positif
Tanda ketidaksamaan soal ≤ 0, maka penyelesaian pada interval yang hasilnya negatif yaitu x < -1 atau -½ ≤ x < 0 atau 0 < x ≤ 5
Jawaban : b
a.{x| x < -5 atau 3,5 < x < 5}
b. {x| x < -√5 atau √5 < x < 3,5}
c. {x|-5 < x < 3,5 atau x > 5}
d. {x|-√5 < x < √5 atau x > 3,5}
Pembahasan :
Pembuat nol
2x - 7=0, x=3,5
x + √5=0, x=-√5
x - √5=0, x=√5
Interval x < -√5; -√5 < x < √5; √5 < x < 3,5; x > 3,5
untuk interval x < -√5, ambil angka uji -3
(2(-3)-7) : [(-3+√5)(-3-√5)]
=(-) : [(-) (-)]=(-) bernilai negatif
untuk -√5 < x < √5 bernilai positif
untuk √5 < x < 3,5 bernilai negatif
untuk x > 3,5 bernilai positif
Tanda ketidaksamaan soal > 0, maka penyelesaian pada interval yang hasilnya positif yaitu -√5 < x < √5 atau x > 3,5
Jawaban : d
a.{x| x < -2 atau 0 < x < 2}
b.{x| -2 < x < 0 atau x > 2}
c.{x| -4 < x < 2 dan x ≠ 0}
d. {x| -2 < x < 2 dan x ≠ 0}
Pembahasan :
Pembuat nol
x²=0, x=0
-x² + 2x - 4=definit negatif
x²+4=definit positif
x + 2=0. x=-2
x - 2=0, x=2
Interval x < -2; -2 < x < 0; 0 < x < 2; x > 2
untuk x < -2, ambil angka uji -3
(-3)²(-) : [(+) (-3+2)(-3-2)]
=(+)(-) : [(+) (-)(-)]=(-) bernilai negatif
untuk -2 < x < 0 bernilai positif
untuk 0 < x < 2 bernilai positif
untuk x > 2 bernilai negatif
Tanda ketidaksamaan soal > 0, maka penyelesaian pada interval yang hasilnya positif yaitu -2 < x < 0 atau 0 < x < 2, dapat dituliskan -2 < x < 2 dan x ≠ 0.

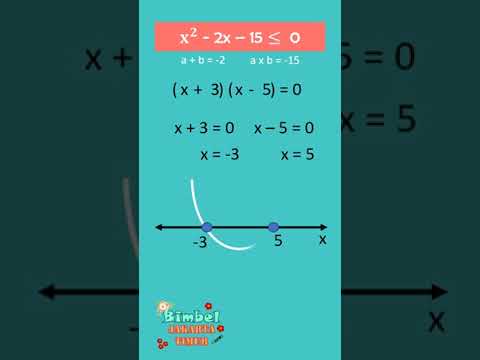
















































.webp)

.webp)