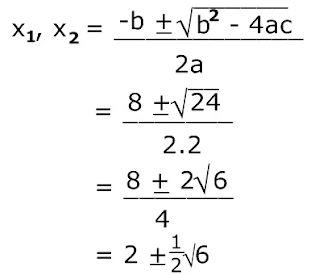Pertidaksamaan adalah suatu kalimat matematika yang menggunakan tanda ketidaksamaan. Tanda ketidaksamaan itu adalah <, >, ≤ atau ≥. Pertidaksamaan kuadrat adalah bentuk pertidaksamaan yang memuat kalimat matematika dengan derajat tertinggi variabelnya adalah dua.
Pertidaksamaan kuadrat memiliki bentuk umum yaitu
ax² + bx + c < 0
ax² + bx + c > 0
ax² + bx + c ≤ 0
ax² + bx + c ≥ 0
Langkah Penyelesaian :
1. Jika soal belum berbentuk persamaan umum, maka ubahlah dulu ke dalam bentuk umum pertidaksamaan kuadrat
contoh : x(x+3) < 2(3x+5)
dikalikan menjadi : x² + 3x < 6x + 10
kumpulkan di satu ruas : x² + 3x - 6x - 10 < 0
bentuk pertidaksamaan umum : x² - 3x - 10 < 0
2. Tentukan pembuat nol dengan terlebih dahulu pergunakan tanda = dan faktorkan. Jika tidak dapat difaktorkan, bisa gunakan rumus abc atau kuadrat sempurna seperti yang pernah kamu pelajari di kelas 9.
contoh : x² - 3x - 10 < 0
Gunakan tanda = : x² - 3x - 10 = 0
Faktorkan : (x + 2) (x - 5) = 0
Tentukan nilai x : x + 2 = 0, maka x = -2
x - 5 = 0, maka x = 5
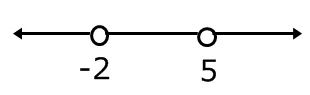
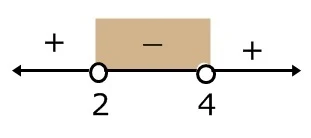
3. Gambar pembuat nol pada garis bilangan. Ingat angka yang lebih kecil harus diletakkan di sebelah kiri. Titik pembuat nol digambarkan dengan bulatan. Jika pada soal tanda ketidaksamaan adalah < atau >, maka bulatan berbentuk lingkaran kosong (⚪). Jika pada soal tanda ketidaksamaan adalah ≤ atau ≥, maka bulatan berbentuk lingkaran isi (⚫).
4. Uji nilai pada setiap daerah garis bilangan yang telah dibagi oleh pembuat nol. Gunakan angka yang mudah dihitung. Umumnya tanda nilai uji berseling +, _, + atau -, +, - kecuali nilai pembuat nol adalah angka kembar.
contoh :
x < -2, ambil -3 sebagai titik uji
x² - 3x - 10 = (-3)² - 3(-3) - 10
= 8 (bernilai +)
-2 < x < 5, ambil angka 0 sebagai titik uji
x² - 3x - 10 = (0)² - 3(0) - 10
= -10 (bernilai -)
x > 5 , ambil angka 6 sebagai titik uji
x² - 3x - 10 = 6² - 3(6) - 10
= 8 (bernilai +)
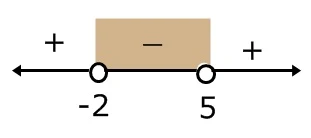
karena pada soal adalah x² - 3x - 10 < 0 , himpunan penyelesaiannya adalah daerah yang menghasilkan nilai negatif. Seperti gambar berikut :
5. Tentukan himpunan penyelesaian
HP = {x| -2 < x < 5}
Semoga pendahuluan di atas dapat kamu pahami. Selanjutnya supaya kamu dapat lebih mahir, latihlah dengan soal-soal di bawah ini
1. Perhatikan pernyataan-pernyataan berikut :
I. x² + 3x - 18 = 0
II. x(x-5) + 3 < 0
III. x³ - 2x² + 5 > 0
IV. 2x² + 3x - 6 ≤ x² - 1
Yang merupakan pertidaksamaan kuadrat adalah....
a. I dan III
b. II dan IV
c. I, II dan III
d. IV saja
Pembahasan :
I. x² + 3x - 18 = 0
menggunakan tanda =
bukan pertidaksamaan
II. x(x-5) + 3 < 0
diuraikan menjadi x² - 5x + 3 < 0
pertidaksamaan kuadrat
III. x³ - 2x² + 5 > 0
pangkat tertinggi 3
bukan pertidaksamaan kuadrat
IV. 2x² + 3x - 6 ≤ x² - 1
Disederhanakan menjadi
2x² + 3x - 6 - x² + 1 ≤ 0
x² + 3x - 5 ≤ 0
pertidaksamaan kuadrat
Jawaban : b
2. Himpunan penyelesaian dari x² ≥ 7x - 10, x ∈ R adalah...
a. { x | x ≤ -2 atau x ≥ 5}
b. { x | x ≤ 2 atau x ≥ 5}
c. { x | -2 ≤ x ≤ 5}
d. { x | 2 ≤ x ≤ 5}
Pembahasan :
x² ≥ 7x - 10
x² - 7x + 10 ≥ 0
Pembuat nol
x² - 7x + 10 = 0
(x-2) (x-5) = 0
x = 2 dan x = 5
untuk x ≤ 2, gunakan angka 1
x² - 7x + 10 = 1² - 7(1) + 10
= 1 - 7 + 10 = 4
bernilai positif
untuk 2 ≤ x ≤ 5, gunakan angka 3
x² - 7x + 10 = 3² - 7(3) + 10
= 9 - 21 + 10
= - 2
bernilai negatif
untuk x ≥ 5, gunakan angka 6
x² - 7x + 10 = 6² - 7(6) + 10
= 36 - 42 + 10
= 4
bernilai positif
Tanda ketidaksamaan ≥ 0, maka himpunan penyelesaian adalah daerah yang bertanda positif
{ x | x ≤ 2 atau x ≥ 5}
Jawaban : b
3. Himpunan penyelesaian dari 3x² < 12 , x ∈ R adalah....
a. { x | x < -2 atau x > 2}
b. { x | x < -3 atau x > 12}
c. { x | -2 < x < 2}
d. { x | -3 < x < 12}
Pembahasan :
3x² < 12
3x² - 12 < 0
Pembuat nol
3x² - 12 = 0
3 (x+2) (x-2) = 0
x = -2 dan x = 2
untuk x < -2, gunakan angka -3
3x² - 12 = 3(-3)² - 12
= 27 - 12 = 15
bernilai positif
untuk -2 < x < 2, gunakan angka 0
3x² - 12 = 3(0)² - 12
= 0 - 12 = -12
bernilai negatif
untuk x > 2, gunakan angka 3
3x² - 12 = 3(3)² - 12
= 27 - 12 = 15
bernilai positif
Tanda ketidaksamaan < 0, maka himpunan penyelesaian adalah daerah yang bertanda negatif.
HP = { x | -2 < x < 2}
Jawaban : c
4. Himpunan penyelesaian dari x² - 8x + 15 ≤ 0, x ∈ R adalah...
a. {x | 3 ≤ x ≤ 5, x ∈ R}
b. {x | -5 ≤ x ≤ -3, x ∈ R}
c. {x | x ≤ -5 atau x ≥ -3, x ∈ R}
d. {x | x ≤ 3 atau x ≥ 5, x ∈ R}
Pembahasan :
Pembuat nol
x² - 8x + 15 = 0
(x-3) (x-5) = 0
x = 3 dan x = 5
untuk x ≤ 3, gunakan angka 0
x² - 8x + 15 = 0² - 8(0) + 15
= 0 - 0 + 15 = 15
bernilai positif
untuk 3 ≤ x ≤ 5, gunakan angka 4
x² - 8x + 15 = 4² - 8(4) + 15
= 16 - 32 + 15 = -1
bernilai negatif
untuk x ≥ 5, gunakan angka 6
x² - 8x + 15 = 6² - 8(6) + 15
= 36 - 48 + 15 = 3
bernilai positif
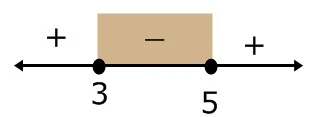
Tanda ketidaksamaan ≤ 0, maka himpunan penyelesaian adalah daerah yang bertanda negatif
HP = {x | 3 ≤ x ≤ 5, x ∈ R}
Jawaban : a
5. Himpunan penyelesaian dari 2x² + x - 15 > 0, x ∈ R adalah...
a. { x | x < -2 atau x > 5/2}
b. { x | x < -3 atau x > 5/2}
c. { x | -2 < x < 5/2}
d. { x | -3 < x < 5/2}
Pembahasan :
Pembuat nol
2x² + x - 15 = 0
(2x-5) (x+3) = 0
x = 5/2 dan x = -3
untuk x < -3, gunakan angka -4
2x² + x - 15 = 2(-4)² + (-4) - 15
= 32 - 4 - 15 = 13
bernilai positif
untuk -3 < x < 5/2, gunakan angka 0
2x² + x - 15 = 2(0)² + 0 - 15
= - 15
bernilai negatif
untuk x > 5/2, gunakan angka 3
2x² + x - 15 = 2(3)² + 3 - 15
= 18 + 3 - 15 = 6
bernilai positif
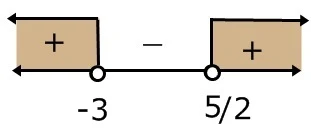
Tanda ketidaksamaan > 0, maka himpunan penyelesaian adalah daerah yang bertanda positif.
HP = { x | x < -3 atau x > 5/2}
Jawaban : b
6. Himpunan penyelesaian dari 2x(x - 3) < x² - 8, x ∈ R adalah...
a. { x | x < -2 atau x > 4}
b. { x | x < 2 atau x > 4}
c. { x | -2 < x < 4}
d. { x | 2 < x < 4}
Pembahasan :
2x(x - 3) < x² - 8
2x² - 6x - x² + 8 < 0
x² - 6x + 8 < 0
Pembuat nol
x² - 6x + 8 = 0
(x-2) (x-4) = 0
x = 2 dan x = 4
untuk x < 2, gunakan angka 0
x² - 6x + 8 = 0² - 6(0) + 8
= 8
bernilai positif
untuk 2 < x < 4, gunakan angka 3
x² - 6x + 8 = 3² - 6(3) + 8
= 9 - 18 + 8 = -1
bernilai negatif
untuk x > 4, gunakan angka 5
x² - 6x + 8 = 5² - 6(5) + 8
= 25 - 30 + 8 = 3
bernilai positif
Tanda ketidaksamaan < 0, maka himpunan penyelesaian adalah daerah yang bertanda negatif.
HP = { x | 2 < x < 4}
Jawaban : d
7. Himpunan penyelesaian dari x² + 4x - 9 ≥ 0, x ∈ R adalah...
a. {x | -√13 - 2 ≤ x ≤ √13 -2}
b. {x | √13 - 2 ≤ x ≤ √13 + 2}
c. {x | x ≤-√13 - 2 atau x ≥ √13 - 2}
d. {x | x ≤ √13 - 2 atau x ≥ √13 + 2 }
Pembahasan :
Pembuat nol
x² + 4x - 9 = 0
tidak dapat difaktorkan, maka pergunakan rumus abc atau kuadrat sempurna
menggunakan kuadrat sempurna
x² + 4x = 9
x² + 4x + (4/2)² = 9 + (4/2)²
x² + 4x + 4 = 9 + 4
(x+2)² = 13
x + 2 = ±√13
x = - √13 - 2 dan x = √13 - 2
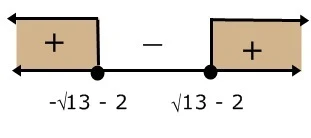
untuk x ≤ - √13 - 2, gunakan angka -6
x² + 4x - 9 = (-6)² + 4(-6) - 9
= 36 - 24 - 9 = 3
bernilai positif
untuk - √13 - 2 ≤ x ≤ √13 - 2, gunakan angka 0
x² + 4x - 9 = 0² + 4(0) - 9
= - 9
bernilai negatif
untuk x ≥ √13 - 2, gunakan angka 2
x² + 4x - 9 = 2² + 4(2) - 9
= 4 + 8 - 9 = 3
bernilai positif
HP = {x | x ≤-√13-2 atau x ≥ √13-2}
Jawaban : c
8. Himpunan penyelesaian dari 2x² - 8x + 5 ≤ 0, x ∈ R adalah...
a. {x | 2 - ½√6 ≤ x ≤ 2 + ½√6}
b. {x | 4 - √6 ≤ x ≤ 4 + √6}
c. {x | x ≤ 2 - ½√6 atau x ≥ 2 + ½√6}
d. {x | x ≤ 4 - √6 atau x ≥ 4 + √6}
Pembahasan :
Pembuat nol
2x² - 8x + 5 = 0
idak dapat difaktorkan, maka pergunakan rumus abc atau kuadrat sempurna
menggunakan rumus abc
a = 2, b = -8, c = 5
b² - 4ac = (-8)² - 4.2.5
= 64 - 40 = 24
Rumus abc
x = 2 - ½√6 dan x = 2 + ½√6
untuk x ≤ 2 - ½√6, gunakan angka -1
2x² - 8x + 5 = 2(-1)² - 8(-1) +5
= 2 + 8 + 5 = 15
bernilai positif
untuk 2 - ½√6 ≤ x ≤ 2 + ½√6, gunakan angka 1
2x² - 8x + 5 = 2(1)² - 8(1) + 5
= 2 - 8 + 5 = - 1
bernilai negatif
untuk x ≥ 2 + ½√6, gunakan angka 4
2x² - 8x + 5 = 2(4)² - 8(4) + 5
= 32 - 32 + 5 = 5
bernilai positif
Tanda ketidaksamaan ≤ 0, maka himpunan penyelesaian adalah daerah yang bertanda negatif
Hp = {x | 2 - ½√6 ≤ x ≤ 2 + ½√6}
Jawaban : a
9. Himpunan penyelesaian dari -2x² - x + 6 > 0, x ∈ R adalah...
a. {x | -2 < x < -3/2}
b. {x | -2 < x < 3/2}
c. {x | x < -2 atau x > -3/2}
d. {x | x < -2 atau x > 3/2}
Pembahasan :
-2x² - x + 6 > 0 (dikalikan -1 agar koefisien x² menjadi positif)
2x² + x - 6 < 0 (karena dikali angka negatif, maka tanda berbalik arah)
Pembuat nol :
2x² + x - 6 = 0
(2x-3) (x+2) = 0
x = 3/2 dan x = -2
untuk x < -2, gunakan angka -3
2x² + x - 6 = 2(-3)² + (-3) - 6
= 18 - 3 - 6 = 9
bertanda positif
untuk -2 < x < 3/2, gunakan angka 0
2x² + x - 6 = 2(0)² + 0 - 6
= - 6
bertanda negatif
untuk x > 3/2, gunakan angka 2
2x² + x - 6 = 2(2)² + 2 - 6
= 10 - 6 = 4
bertanda positif
Tanda kesamaan yang digunakan < 0, maka himpunan penyelesaian yang bernilai negatif
Hp = {x | -2 < x < 3/2}
Jawaban : b
10. Himpunan penyelesaian dari 3x² ≤ 10 - x, x ∈ R adalah...
a. {x| -2 ≤ x ≤ 5/3}
b. {x| -2 ≤ x ≤ 3/5}
c. {x| x ≤ -2 atau x ≥ 5/3}
d. {x| x ≤ -2 atau x ≥ 3/5}
Pembahasan :
3x² ≤ 10 - x
3x² + x - 10 ≤ 0
Pembuat nol
3x² + x - 10 = 0
(3x-5) (x + 2) = 0
x = 5/3 dan x = -2
untuk x ≤ -2, gunakan angka -3
3x² + x - 10 = 3(-3)² + (-3) - 10
= 27 - 3 - 10 = 14
bertanda positif
untuk -2 ≤ x ≤ 5/3, gunakan angka 0
3x² + x - 10 = 3(0)² + 0 - 10
= - 10
bertanda negatif
untuk x ≥ 5/3, gunakan angka 2
3x² + x - 10 = 3(2)² + 2 - 10
= 12 + 2 - 10 = 4
bertanda positif
Tanda ketidaksamaan ≤ 0, maka himpunan penyelesaian adalah daerah yang bertanda negatif
HP = {x| -2 ≤ x ≤ 5/3}
Jawaban : a
11. Batas nilai p yang memenuhi agar persamaan x² - (p-1)x + (p-2) = 0 mempunyai dua akar real yang berbeda adalah...
a. {p| 1 < p < 5}
b. {p| 2 < p < 3}
c. {p| p < 1 atau p > 5}
d. {p| p < 2 atau p > 3}
Pembahasan :
Supaya persamaan x² - (p-1)x + (p-1) = 0 mempunyai dua akar real yang berbeda, maka nilai D harus > 0
a = 1, b = -(p-1), c = (p-1)
D = b² - 4ac
[-(p-1)]² - 4.1.(p-1) > 0
p² - 2p + 1 - 4p + 4 > 0
p² - 6p + 5 > 0
Pembuat nol
p² - 6p + 5 = 0
(p -1) (p-5) = 0
p = 1 dan p = 5
untuk p < 5, gunakan angka 0
p² - 6p + 5 = 0² - 6(0) + 5
= 5
bernilai positif
untuk 1 < p < 5, gunakan angka 2
p² - 6p + 5 = 2,² - 6(2) + 5
= 4 - 12 + 5
= -3
bernilai negatif
untuk p > 5, gunakan angka 6
p² - 6p + 5 = 6² - 6(6) + 5
= 36 - 36 + 5
= 5
bernilai positif
Tanda ketidaksamaan > 0, maka himpunan penyelesaian adalah yang bernilai positif
HP = {p| p < 1 atau p > 5}
Jawaban : c
12. Batas nilai m yang memenuhi agar persamaan (m-5)x² - 4mx + m - 2 = 0 tidak memiliki akar real adalah....
a. {m| 10/3 < m < 1}
b. {m| -10/3 < m < 1}
c. {m| m < -10/3 atau m > 1}
d. {m| m < 10/3 atau m > 1}
Pembahasan :
Supaya persamaan (m-5)x² - 4mx + m - 2 = 0 tidak memiliki akar real, maka nilai D harus < 0
a = m-5, b = -4m, c = m-2
b² - 4ac < 0
(-4m)² - 4 (m-5) (m-2) < 0
16m² - 4m² + 28m - 40 < 0
12m² + 28m - 40 < 0
Pembuat nol
12m² + 28m - 40 = 0 (sederhanakan)
3m² + 7m - 10 = 0
(3m + 10) (m -1) = 0
m = -10/3 dan m = 1
untuk m < -10/3, gunakan angka -4
3m² + 7m - 10 = 3(-4)² + 7(-4) - 10
= 48 - 28 - 10 = 10
bernilai positif
untuk -10/3 < m < 1, gunakan angka 0
3m² + 7m - 10 = 3(0)² + 7(0) - 10
= -10
bernilai negatif
untuk m > 1, gunakan angka 2
3m² + 7m - 10 = 3(2)² + 7(2) - 10
= 12 + 14 - 10 = 16
bernilai positif
Tanda kesamaan yang digunakan < 0, maka himpunan penyelesaian yang bernilai negatif
HP = {m| -10/3 < m < 1}
Jawaban : b
13. Pak Rahman akan membuat kolam ikan di sebagian tanah miliknya. Ia mempunyai bahan untuk membuat kolam dengan keliling 28 m. Jika Pak Rahman menginginkan luas kolam renangnya tidak kurang dari 45 m², berapa batas panjang kolam renang yang dapat dibuat?
a. p ≤ 5 atau p ≥ 9
b. 5 ≤ p ≤ 9
c. p ≤ 6 atau p ≥ 8
d. 6 ≤ p ≤ 8
Pembahasan :
Keliling = 28 m
2(p+l) = 28
p + l = 14
l = 14 - p
Luas kolam renangnya tidak kurang dari 45 m², artinya bisa sama dengan atau lebih. Tanda yang dipakai adalah ≥ 45
Luas ≥ 45
p x l ≥ 45
p(14-p) ≥ 45
14p - p² - 45 ≥ 0 (kalikan dengan -1)
p² - 14p + 45 ≤ 0
Pembuat nol
p² - 14p + 45 = 0
(p-5) (p-9) = 0
untuk p ≤ 5
p² - 14p + 45 = 0² - 14(0) + 45 = 45
bernilai positif
untuk 5 ≤ p ≤ 9
p² - 14p + 45 = 6² - 14(6) + 45
= 36 - 84 + 45 = -3
bernilai negatif
untuk p ≥ 9
p² - 14p + 45 = 10² - 14(10) + 45
= 100 - 140 + 45 = 5
bernilai positif
Derah yang memenuhi untuk p² - 14p + 45 ≤ 0 adalah 5 ≤ p ≤ 9
Jawaban : b
14. Sebuah peluru ditembakkan ke atas dengan persamaan ketinggian adalah h(t) = 47t - 2t² (dengan h dalam meter dan t dalam detik). Berapa lama peluru itu mencapai ketinggian di atas 240 m?
a. 6 detik
b. 7,5 detik
c. 8,5 detik
d. 16 detik
Pembahasan :
Ketinggian di atas 240 m berarti > 240
47t - 2t² > 240
47t - 2t² - 240 > 0 (kalikan dengan -1)
2t² - 47t + 240 < 0
Pembuat nol :
2t² - 47t + 240 = 0
(2t - 15) (t - 16) = 0
t = 7,5 dan t = 16
untuk t < 7,5
2t² - 47t + 240 = 2(0)² - 47(0) + 240 = 240
bernilai positif
untuk 7,5 < t < 16
2t² - 47t + 240 = 2(10)² - 47(10) + 240
= 200 - 470 + 240 = - 30
bernilai negatif
untuk x > 16
2t² - 47t + 240 = 2(20)² - 47(20) + 240
= 800 - 940 + 240 = 100
bernilai positif
Karena yang dihitung adalah pertidaksamaan akhir yang bertanda < 0, maka yang memenuhi adalah yang bernilai negatif
7,5 < t < 16
Peluru berada di atas ketinggian 240 m antara detik ke 7,5 dan 16
Lamanya adalah 16 - 7,5 = 8,5 detik
Jawaban : c
15. Ane akan menggambar segitiga siku-siku yang panjang sisi siku-sikunya berselisih 4 cm. Jika ia menginginkan panjang hipotenusa tidak kurang dari 20 cm, maka batas panjang sisi terpendek dari segitiga itu adalah....
a. x ≤ -16
b. x ≥ 12
c. x ≤ -16 atau x ≥ 12
d. -16 ≤ x ≤ 12
Pembahasan :
Misalkan sisi terpendek adalah x, maka sisi segitiga yang lain adalah x + 4.
Panjang hipotenusa tidak kurang dari 20, artinya ≥ 20
Panjang hipotenusa menggunakan rumus phytagoras seperti berikut
x² + (x+4)² ≥ 20²
x² + x² + 8x + 16 ≥ 400
2x² + 8x + 16 - 400 ≥ 0
2x² + 8x - 384 ≥ 0 (sederhanakan)
x² + 4x - 192 ≥ 0
(x + 16) (x - 12) = 0
x = -16 atau x = 12
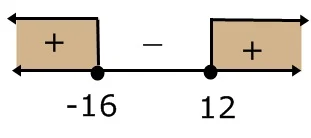
untuk x ≤ -16, ambil nilai uji -17
(-17)² + 4(-17) - 192 = 29 (bernilai positif)
untuk -16 ≤ x ≤ 12, ambil nilai uji 0
0² + 4(0) - 192 = - 192 (bernilai negatif)
Untuk x ≥ 12, ambil nilai uji 13
13² + 4(13) - 192 = 29 (bernilai positif)
b. x ≥ 12
c. x ≤ -16 atau x ≥ 12
d. -16 ≤ x ≤ 12
Pembahasan :
Misalkan sisi terpendek adalah x, maka sisi segitiga yang lain adalah x + 4.
Panjang hipotenusa tidak kurang dari 20, artinya ≥ 20
Panjang hipotenusa menggunakan rumus phytagoras seperti berikut
x² + (x+4)² ≥ 20²
x² + x² + 8x + 16 ≥ 400
2x² + 8x + 16 - 400 ≥ 0
2x² + 8x - 384 ≥ 0 (sederhanakan)
x² + 4x - 192 ≥ 0
(x + 16) (x - 12) = 0
x = -16 atau x = 12
untuk x ≤ -16, ambil nilai uji -17
(-17)² + 4(-17) - 192 = 29 (bernilai positif)
untuk -16 ≤ x ≤ 12, ambil nilai uji 0
0² + 4(0) - 192 = - 192 (bernilai negatif)
Untuk x ≥ 12, ambil nilai uji 13
13² + 4(13) - 192 = 29 (bernilai positif)
Karena tanda ketidaksamaan dalam soal adalah ≥ 0, maka himpunan penyelesaian adalah yang bernilai positif yaitu x ≤ -16 atau x ≥ 12.
Tetapi kamu juga harus mencermati bahwa hal yang dibicarakan dalam soal adalah panjang sisi, sehingga tidak mungkin bernilai negatif. Maka batas sisi terpendek yang memenuhi adalah x ≥ 12.
Tetapi kamu juga harus mencermati bahwa hal yang dibicarakan dalam soal adalah panjang sisi, sehingga tidak mungkin bernilai negatif. Maka batas sisi terpendek yang memenuhi adalah x ≥ 12.
Demikian sedikit ringkasan materi beserta soal latihan tentang Pertidaksamaan Kuadrat yang dapat kami sajikan. Semoga berguna untuk siswa yang sedang mempelajari materi ini.