Soal Pertidaksamaan Irasional By Bimbel Jakarta Timur

Pertidaksamaan Irasional adalah bentuk pertidaksamaan, yang memiliki fungsi dalam tanda akar baik fungsi di ruas kiri, fungsi di ruas kanan atau di kedua ruasnya. Pertidaksamaan irasional terdefinisi jika syarat-syaratnya terpenuhi yaitu jika fungsi dalam akar besarnya lebih besar atau sama dengan nol.


1. Nilai x yang memenuhi adalah...

Pembahasan :
kuadratkan kedua ruas

x + 5 < 9

x < 9 - 5

x < 4

syarat :

x + 5 ≥ 0

x ≥ - 5

Maka nilai x yang memenuhi adalah -5 ≤ x < 4

2. Nilai x yang memenuhi  adalah...

Pembahasan : 
kuadratkan kedua ruas 

2x - 1 > 25
2x > 25 + 1
2x > 26
x > 13

syarat :
2x - 1 ≥ 0
2x ≥ 1
  x ≥ 1/2

Maka nilai x yang memenuhi adalah x > 13

3. Himpunan penyelesaian dari  adalah.....

Pembahasan :
kedua ruas dikuadratkan menjadi
4 - 3x ≥ x²
- x² - 3x + 4 ≥ 0 (kalikan dengan -1)
x² + 3x - 4 ≤ 0
(x + 4) (x - 1) ≤ 0

pembuat nol
x + 4=0, x=-4
x - 1=0, x=1
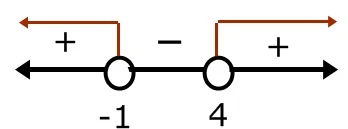
interval x ≤ -4, -4 ≤ x ≤ 1, x ≥ 1

untuk interval -4 ≤ x ≤ 1, titik uji 0
0² + 3(0) - 4=-4 (negatif)
maka
x ≤ -4 positif
-4 ≤ x ≤ 1 negatif
 x ≥ 1 positif

syarat :
4 - 3x ≥ 0
   - 3x ≥ - 4
       x ≤ 4/3

HP={x| x ≤ -4  atau 1 ≤ x ≤ 4/3}

4. Himpunan penyelesaian dari  adalah....
Pembahasan :
Kuadratkan kedua ruas
x + 5 > x² - 2x + 1
x + 5 - x² + 2x - 1 > 0
- x² + 3x + 4 > 0
x² - 3x - 4 > 0
(x + 1) (x - 4) > 0

Pembuat nol
x + 1=0, x=-1
x - 4=0, x=4
interval x < -1, -1 < x < 4, x > 4

untuk -1 < x < 4, titik uji 0
0² - 3(0) - 4=-4 (negatif)
maka
x < -1 positif
-1 < x < 4 negatif 
x > 4 positif

syarat :
x + 5 ≥ 0
x ≥  -5

HP={x| -5 ≤ x < -1 atau x > 4

5. Himpunan penyelesaian dari  adalah....
Pembahasan :
pindahkan x ke ruas kanan lalu kuadratkan kedua ruas
< x + 1
3x + 7 < x² + 2x + 1
3x + 7 - x² - 2x - 1 < 0
- x² + x + 6 < 0 dikali -1, tanda berbalik arah
x² - x - 6 > 0

pembuat nol
x² - x - 6=0
(x + 2) (x - 3)=0
x=-2, x=3
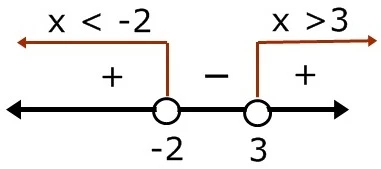
interval x < -2, -2 < x < 3, x > 3

untuk -2 < x < 3 titik uji 0
0² - 0 - 6=negatif, maka
x < -2 positif
x > 3 positif

syarat :
3x + 7 ≥ 0
3x ≥ -7
x  ≥ -7/3

HP={x| -7/3 ≤ x < -2 atau x > 3}

6. Himpunan penyelesaian dari  adalah....

Pembahasan :
kuadratkan kedua ruas
x - 1 ≤ x² - 6x + 9
x - 1 - x² + 6x - 9 ≤ 0 
- x² + 7x - 10 ≤ 0
 x² - 7x + 10 ≥ 0

pembuat nol
x² - 7x + 10=0
(x - 2) (x - 5)=0
x=2, x=5
interval  x ≤ 2, 2 ≤ x ≤ 5, x ≥ 5

untuk x ≤ 2 titik uji 0
0² - 0x + 10=10 (positif), maka
2 ≤ x ≤ 5 negatif
x ≥ 5 positif

syarat :
x - 1 x ≥ 0
x  ≥ 1

HP={x| 1 ≤ x ≤ 2 atau x ≥ 5}

7. Himpunan penyelesaian dari  adalah....

Pembahasan :

x² - 7x + 10 < 4
x² - 7x + 10 - 4 < 0
x² - 7x + 6 < 0

pembuat nol
x² - 7x + 6=0
(x - 1) (x - 6)=0
x=1, x=6
interval x < 1, 1 < x < 6, x > 6

untuk x < 1 titik uji 0
0² - 7(0) + 6=6 (positif), maka
1 < x < 6 negatif 
x > 6 positif

syarat : 
x² - 7x + 10 ≥ 0

pembuat nol
x² - 7x + 10=0
(x - 2) (x - 5)=0
x=2, x=5
interval x ≤ 2, 2 ≤ x ≤ 5, x ≥ 5

untuk x ≤ 2 titik uji 0
0² - 7(0) + 10=10 (positif), maka
2 ≤ x ≤ 5 negatif
x ≥ 5 positif

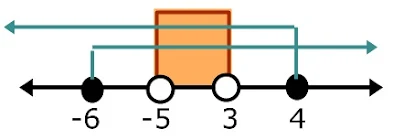
kedua garis bilangan digabung lalu tentukan irisannya

HP={x| -1 < x ≤ 2 atau 5 ≤ x < 6}

8. Himpunan penyelesaian dari  adalah....
Pembahasan :

x² + 6x - 7 < 9
x² + 6x - 7 - 9 < 0
x² + 6x - 16 < 0

pembuat nol
x² + 6x - 16=0
(x + 8) (x - 2)=0
x=-8, x=2
interval x < -8, -8 < x < 2, x > 2

untuk -8 < x < 2 titik uji 00² + 6(0) - 16=- 16 (negatif), maka
x < -8 positif
x > 2 positif

syarat :

x² + 6x - 7 ≥ 0

pembuat nol
x² + 6x - 7=0
(x + 7) (x - 1)=0
x=-7, x=1
interval x ≤ -7, -7 ≤ x ≤ 1, x ≥ 1

untuk -7 ≤ x ≤ 1 titik uji 0
0² + 6(0) - 7=-7 (negatif), maka
x ≤ -7 positif
x ≥ 1 positif

kedua garis bilangan digabung lalu tentukan irisannya

HP= {x| -8 < x ≤ -7 atau 1 ≤ x < 2}

9. Himpunan penyelesaian dari  adalah.....

Pembahasan :

syarat 1 :

kuadratkan kedua ruas

3x + 2 < x + 6

3x - x < 6 - 2

2x < 4

x < 2

syarat 2 :

3x + 2 ≥ 0

3x ≥ -2

x ≥ -2/3

syarat 3 :

x + 6 ≥ 0

x ≥ -6

HP={x| -2/3 ≤ x < 2}

10. Himpunan penyelesaian dari  adalah.....

Pembahasan : 

syarat 1 :

kuadratkan kedua ruas

2x - 5 > 4 - x

2x + x > 4 + 5

3x > 9

x > 3

syarat 2 :

2x - 5 ≥ 0

2x ≥ 5

x ≥ 5/2

syarat 3 :

4 - x ≥ 0

  -x ≥ -4

   x ≤ 4

HP={x| 3 < x ≤ 4}

11. Himpunan penyelesaian dari adalah...

Pembahasan :
syarat 1 :
> 2 -  (kuadratkan kedua ruas)
6 - x  > 4 - 4 + x + 4
4 > 8 + x - 6 + x
4 > 2 + 2x
2 > x + 1 
4 (x + 4) > x² + 2x + 1
4x + 16 - x² - 2x - 1> 0
-x² + 2x + 15 > 0
x² - 2x - 15 < 0

pembuat nol
x² - 2x - 15=0
(x + 3) (x - 5)=0
x=-3, x=5
interval x < -3, -3 < x < 5, x > 5

untuk -3 < x < 5 titik uji 0
0² - 2(0) - 15=-15 (negatif)
x < -3 positif
x > 5 positif
Tanda ketidaksamaan < 0, daerah yang memenuhi -3 < x < 5

syarat 2 :
6 - x ≥ 0
- x ≥ - 6
x ≤ 6

syarat 3 :
x + 4 ≥ 0
x ≥ - 4

HP={x| -5 < x < 3}

12. Nilai x yang memenuhi  adalah....

Pembahasan :
syarat 1
3x + 7 ≥ 0
3x ≥ - 7
x ≥ -7/3

syarat 2 :

1 < 3x + 7
-3x < 7 - 1
-3x < 6
x > -2

syarat 3 :

3x + 7 < 4
3x < 4 - 7
3x < - 3
x < -1

HP={x| -2 < x < -1}

13. Nilai x yang memenuhi  adalah....

Pembahasan :

syarat 1 :
x² + 2x < 5x
x² - 3x < 0

pembuat nol
x² - 3x=0
x (x - 3)=0
x=0, x=3
interval x < 0, 0 < x < 3, x > 3

untuk 0 < x < 3 titik uji 1
1² - 3(1)=-2 (negatif)
x < 0 positif
x > 3 positif
Tanda ketidaksamaan < 0, daerah yang memenuhi 0 < x < 3

syarat 2 :
x² + 2x ≥ 0

pembuat nol
x² + 2x=0
x (x + 2)=0
x=0, x=-2
interval x ≤ -2, -2 ≤ x ≤ 0, x ≥ 0

untuk x ≥ 0 titik uji 1
1² + 2(1)=3 positif
x ≤ -2 positif
-2 ≤ x ≤ 0 negatif
Tanda ketidaksamaan ≥ 0, daerah yang memenuhi x ≤ -2 atau x ≥ 0 


syarat 3 :
5x ≥ 0
x ≥ 0

HP={x| 0 < x < 3}

14. Nilai x yang memenuhi   adalah....

Pembahasan :
syarat 1:
 < x - 3
4x < x² - 6x + 9
0 < x² - 10x + 9
x² - 10x + 9 > 0

pembuat nol
x² - 10x + 9=0
(x - 1) (x - 9)=0
x=1, x=9
interval x < 1, 1 < x < 9, x > 9

untuk x < 1 titik uji 0
0² - 10(0) + 9=9 (positif)
1 < x < 9 negatif
x > 9 positif
Tanda ketidaksamaan > 0, daerah yang memenuhi x < 1 atau x > 9

syarat 2:
4x ≥ 0
x ≥ 0

HP={x| 0 ≤ x < 1 atau x > 9}

15. Nilai x yang memenuhi  adalah....

Pembahasan :

syarat 1 :
x² - x - 2 ≥ 0

pembuat nol
x² - x - 2=0
(x - 2) (x + 1)=0
x=2, x=-1
interval x ≤ -1, -1 ≤ x ≤ 2, x ≥ 2

untuk -1 ≤ x ≤ 2 titik uji 0
0² - 0 - 2=- 2 (negatif)
x ≤ -1 positif
x ≥ 2 positif
Tanda ketidaksamaan  ≥ 0, daerah yang memenuhi x ≤ -1 atau x ≥ 2

syarat 2:
x² + 5x + 6 ≥ 0

pembuat nol
x² + 5x + 6=0
(x + 3) (x + 2)=0
x=-3, x=-2
interval x ≤ -3, -3 ≤ x ≤ -2, x ≥ -2

untuk x ≥ -2 titik uji 0
0² + 5(0) + 6=6 (positif)
x ≤ -3 positif
-3 ≤ x ≤ -2 negatif
Tanda ketidaksamaan  ≥ 0, daerah yang memenuhi x ≤ -3 atau x ≥ -2

syarat 3:
x² - x - 2 < x² + 5x + 6
  - x - 5x < 6 + 2
  - 6x   < 8
      x > -4/3

HP={x| -4/3 < x ≤ -1 atau x ≥ 2}

16. Nilai x yang memenuhi  adalah....

Pembahasan :
syarat 1 :

2x² + x - 6 ≥ 0

pembuat nol 
2x² + x - 6=0
(2x - 3) (x + 2)=0
x=3/2, x=-2
interval x ≤ -2, -2 ≤ x ≤ 3/2, x ≥ 3/2

untuk -2 ≤ x ≤ 3/2 titik uji 0
2(0)² + 0 - 6=- 6 (negatif)
x ≤ -2 positif
x ≥ 3/2 positif

Tanda ketidaksamaan  ≥ 0, daerah yang memenuhi x ≤ -2 atau x ≥ 3/2

syarat 2:

x² + x ≥ 0

pembuat nol
x(x+1)=0

x=0, x=-1

interval x ≤ -1, -1 ≤ x ≤ 0, x ≥ 0

untuk x ≥ 0 titik uji 1
1² + 1=2 (positif)
x ≤ -1 positif
-1 ≤ x ≤ 0 negatif

Tanda ketidaksamaan  ≥ 0, daerah yang memenuhi x ≤ -1 atau x ≥ 0

syarat 3 :
2x² + x - 6 < x² + x
x² - 6 < 0

pembuat nol
x² - 6=0
(x + √6) (x - √6)=0
x=-√6, x=√6
interval x < -√6, -√6 < x < √6, x > √6

untuk -√6 ≤ x ≤ √6 titik uji 0
0² - 6=-6 (negatif)
x < -√6 positif
x > √6 positif

Tanda ketidaksamaan < 0, daerah yang memenuhi -√6 < x < √6

HP={x| -√6 < x ≤ -2 atau 3/2 ≤ x < √6}

17. Himpunan penyelesaian dari  adalah....

Pembahasan :
syarat 1 :
2x + 8 ≥ 0
2x ≥ - 8
x ≥ -4

syarat 2 :
kuadratkan kedua ruas
x² > 2x + 8
x² - 2x - 8 > 0

pembuat nol 
x² - 2x - 8=0
(x + 2) (x - 4)=0
x=-2, x=4
interval x < -2, -2 < x < 4, x > 4

untuk -2 < x < 4 titik uji 0
0² - 2(0) - 8=-8 (negatif)
x < -2 positif
x > 4 positif
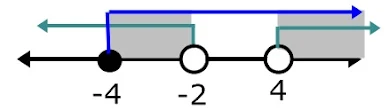
Tanda ketidaksamaan  > 0, daerah yang memenuhi x < -2 atau x > 4

HP={x| -4 ≤ x < -2 atau x > 4}

18. Himpunan penyelesaian dari √x + 2 < x  adalah....

Penyelesaian : 

syarat 1 :
x ≥ 0

syarat 2 :
√x < x - 2
x < x² - 4x + 4
0 < x² - 5x + 4
x² - 5x + 4 > 0

pembuat nol
x² - 5x + 4=0
(x - 1) (x - 4)=0
x=1, x=4
interval x < 1, 1 < x < 4, x > 4

untuk x < 1 titik uji 0
0² - 5(0) + 4=4 (positif) 
1 < x < 4 negatif
x > 4 positif
Tanda ketidaksamaan  > 0, daerah yang memenuhi x < 1 atau x > 4

HP={x| -4 ≤ x < -2 atau x > 4}

19. Himpunan penyelesaian dari  adalah....

Pembahasan :

syarat 1 : 

x² - 4 ≥ 0

pembuat nol

x² - 4=0

(x + 2) (x - 2)=0

x=-2, x=2

interval x ≤ -2, -2 ≤ x ≤ 2, x ≥ 2

untuk -2 ≤ x ≤ 2 titik uji 0
0² - 4=-4 (negatif)
x ≤ -2 positif
x ≥ 2 positif

Tanda ketidaksamaan ≥ 0, daerah yang memenuhi x ≤ -2 atau x ≥ 2

syarat 2:
x² - 4 < 4
x² - 8 < 0

pembuat nol
x² - 8=0
(x + 2√2)(x - 2√2)=0
x=-2√2, x=2√2

interval x < -2√2, -2√2 < x < 2√2, x > 2√2

untuk -2√2 < x < 2√2 titik uji 0
0² - 8=-8 (negatif) 
x < - 2√2 positif
x > 2√2 positif
Tanda ketidaksamaan x < 0, daerah yang memenuhi - 2√2 < x < 2√2 

HP={x| -2√2 < x ≤ -2 atau 2 ≤ x < 2√2}

20. Himpunan penyelesaian dari  adalah....

Pembahasan :

syarat 1 :

pembuat nol

x + 3=0, x=-3

x - 1=0, x=1

interval x ≤ -3, -3 ≤ x ≤ 1, x ≥ 1

untuk -3 ≤ x ≤ 1, titik uji 0

(0+3) : (0-1)=3/-1=-3 (negatif)

x ≤ -3 positif

x ≥ 1 positif

Tanda ketidaksamaan  ≥ 0, daerah yang memenuhi x ≤ -3 atau x ≥ 1

syarat 2 :
x ≥ 0

syarat 3 :

pembuat nol

x - 3=0, x=3
x + 1=0, x=-1

x - 1=0, x=1

interval x ≤ -1, -1 ≤ x ≤ 1, 1 ≤ x ≤3, x ≥ 3

untuk x ≤ -1, titik uji -2
(-2-3) (-2+1) : (-2-1)=(-5)(-1):(-3)=5/-3 (negatif)
-1 ≤ x ≤ 1 positif
1 ≤ x ≤ 3 negatif
x ≥ 3 positif
Tanda ketidaksamaan ≥  0, daerah yang memenuhi  -1 ≤ x ≤ 1 atau x ≥ 3

HP={x| x ≥ 3}

SEMOGA BERMANFAAT

https://www.radarhot.com/2020/08/soal-pertidaksamaan-irasional.html

Bimbel Jakarta Timur

Nemo enim ipsam voluptatem quia voluptas sit aspernatur aut odit aut fugit, sed quia consequuntur magni dolores eos qui ratione voluptatem sequi nesciunt.