Persamaan dan Pertidaksamaan Linear Satu Variabel yang memuat Nilai Mutlak. Dari sudut pandang geometri,
nilai mutlak dari x ditulis | x |, adalah jarak dari x ke 0 pada garis bilangan real. Karena jarak selalu positif atau nol maka nilai mutlak x juga selalu bernilai positif atau nol untuk setiap x bilangan real.
1. Di antara persamaanberikut ini yang merupakan persamaan linear satu variabel adalah ....
a. 2x + 3y=12
b. x² - 9=0
c. 3(2x + 7)=15
d. x(2x - 3) + 16=0
Pembahasan :
a. memiliki dua variabel yaitu x dan y
b. memiliki suku x² yaitu berpangkat dua, bukan linear
c. dijabarkan 3(2x + 7)=15 ⇔ 6x + 21=15 ✓
d. djiabarkan x(2x - 3) + 16=0 ⇔ 2x² - 3x + 16=0 (fungsi kuadrat)
Jawaban : c
2. Nilai xyang memenuhi persamaan 9 - 2x=12 adalah…
a. -3/2
b. -1/2
c. 2/3
d. 3/2
Pembahasan :
9 - 2x=12
- 2x=12 - 9
- 2x=-3
x= -3
-2
x=3/2
Jawaban : d
a. -3/2
b. -1/2
c. 2/3
d. 3/2
Pembahasan :
9 - 2x=12
- 2x=12 - 9
- 2x=-3
x= -3
-2
x=3/2
Jawaban : d
3. Persamaan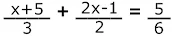 
mempunyai penyelesaian....
a. x=-1/4
b. x=-1/2
c. x=-2
d. x=-4
Pembahasan :
x+5 + 2x-1 = 5 (kali dengan kpk penyebut)
3 2 6
2(x+5) + 3(2x-1)=5
2x + 10 + 6x - 3=5
2x + 6x=5 - 10 + 3
8x =-2
x =-1/4
Jawaban : a
mempunyai penyelesaian....a. x=-1/4
b. x=-1/2
c. x=-2
d. x=-4
Pembahasan :
x+5 + 2x-1 = 5 (kali dengan kpk penyebut)
3 2 6
2(x+5) + 3(2x-1)=5
2x + 10 + 6x - 3=5
2x + 6x=5 - 10 + 3
8x =-2
x =-1/4
Jawaban : a
a. x=3
b. x=3,5
c. x=4
d. x=7
Pembahasan :
5x-1 =3
x + 2
5x-1=3(x+2)
5x-1=3x+6
5x-3x=6+1
2x =7
x =7/2=3,5
Jawaban : b
5. Pak Amin mempunyai sebidang kebun yang berukuran panjang (3x + 1) meter dan lebar 2x meter. Pak Amin membutuhkan kawat sepanjang 82 meter untuk memagari kebun tersebut di sekelilingnya. Ukuran kebun Pak Amin adalah....
a. panjang=21 m, lebar=20 m
b. panjang=23 m, lebar=18 m
c. panjang=25 m, lebar=16 m
d. panjang=27 m, lebar=14 m
Pembahasan :
Keliling=2 (p+l)
82 =2 ((3x+1)+(2x))
82 =6x + 2 + 4x
82 - 2=10x
80 =10x
x=8 m
p=3x + 1=3(8)+1=25 m
l =2x=2(8)=16 m
Jawaban : c
6. Tigabilangan ganjil positif berurutan jumlahnya 81. Hasil kali bilangan terkecil dan terbesarnya adalah....
a. 625
b. 725
c. 729
d. 731
Pembahasan :
Bilangan ganjil berurutan mempunyai selisih 2
Misal : bilangan pertama=a
bilangan kedua=a + 2
bilangan ketiga=a + 4
Jumlah=a + (a+2) + (a+4)
81 =3a + 6
81 - 6=3a
75=3a
a=75/3=25
bilangan terkecil=a=25
bilangan terbesar=a + 4=29
Hasil kali=25 x 29=725
Jawaban : b
a. 625
b. 725
c. 729
d. 731
Pembahasan :
Bilangan ganjil berurutan mempunyai selisih 2
Misal : bilangan pertama=a
bilangan kedua=a + 2
bilangan ketiga=a + 4
Jumlah=a + (a+2) + (a+4)
81 =3a + 6
81 - 6=3a
75=3a
a=75/3=25
bilangan terkecil=a=25
bilangan terbesar=a + 4=29
Hasil kali=25 x 29=725
Jawaban : b
7. Diketahui f(x)=|5x -7|. Himpunan penyelesaian fungsi f(x) untuk daerah asal{x|-1≤ x ≤ 3, x ∈ bilangan bulat}adalah....
a.{-12, -7, -2, 3, 8}
b.{-12, -8, -7, -3, -2}
c. {-2, 3, 7, 8, 12}
d. {2, 3, 7, 8, 12}
Pembahasan :
f(x)=|5x -7|
f(-1)=|5(-1)-7|=|-5-7|=|-12|=12
f(0)=|5(0)-7|=|0-7|=|-7|=7
f(1)=|5(1)-7|=|5-7|=|-2|=2
f(2)=|5(2)-7|=|10-7|=|3|=3
f(3)=|5(3)-7|=|15-7|=|8|=8
Hp={2, 3, 7, 8, 12}
Jawaban : d
b.{-12, -8, -7, -3, -2}
c. {-2, 3, 7, 8, 12}
d. {2, 3, 7, 8, 12}
Pembahasan :
f(x)=|5x -7|
f(-1)=|5(-1)-7|=|-5-7|=|-12|=12
f(0)=|5(0)-7|=|0-7|=|-7|=7
f(1)=|5(1)-7|=|5-7|=|-2|=2
f(2)=|5(2)-7|=|10-7|=|3|=3
f(3)=|5(3)-7|=|15-7|=|8|=8
Hp={2, 3, 7, 8, 12}
Jawaban : d
8. Nilai x yang memenuhi persamaan mutlak |2x - 9|=5 adalah....
a. -2
b. 2
c. -2 dan 7
d. 2 dan 7
Pembahasan :
|2x - 9|=5
2x - 9=5 atau 2x - 9=-5
⇔ 2x - 9=5
2x =5 + 9
2x =14
x =7
⇔ 2x - 9=-5
2x =-5 + 9
2x =4
x =2
Nilai x yang memenuhi adalah 2 dan 7
Jawaban : d
a. -2
b. 2
c. -2 dan 7
d. 2 dan 7
Pembahasan :
|2x - 9|=5
2x - 9=5 atau 2x - 9=-5
⇔ 2x - 9=5
2x =5 + 9
2x =14
x =7
⇔ 2x - 9=-5
2x =-5 + 9
2x =4
x =2
Nilai x yang memenuhi adalah 2 dan 7
Jawaban : d
9. Himpunanpenyelesaian dari |3x - 4|=|x + 18| adalah ....
a. {-3½, 11}
b. {3½, 11}
c. {-3½, -11}
d. {3½, -11}
Pembahasan :
|3x - 4|=|x + 18|
3x - 4=x + 18 atau 3x - 4=-x -18
⇔ 3x - 4=x + 18
3x - x=18 + 4
2x =22
x =11
⇔ 3x - 4=-x -18
3x + x=-18 + 4
4x =-14
x =-14/4
x =-3½
a. {-3½, 11}
b. {3½, 11}
c. {-3½, -11}
d. {3½, -11}
Pembahasan :
|3x - 4|=|x + 18|
3x - 4=x + 18 atau 3x - 4=-x -18
⇔ 3x - 4=x + 18
3x - x=18 + 4
2x =22
x =11
⇔ 3x - 4=-x -18
3x + x=-18 + 4
4x =-14
x =-14/4
x =-3½
Hp={-3½, 11}
Jawaban : a
Jawaban : a
10. Himpunan penyelesaian dari 31− ∣4a−5∣ =20 adalah....
a. {-1½, -11}
b. {1½, -11}
c. {-1½, 11}
d. {1½, 11}
Pembahasan :
31− ∣4a−5∣ =20
− ∣4a−5∣ =20 - 31
- |4a-5|=-11
|4a-5|=11
4a - 5=11 atau 4a - 5=-11
⇔ 4a - 5=11
4a =11 + 5
4a =16
a =4
⇔ 4a - 5=-11
4a =-11 + 5
4a =-6
a =-1½
Hp={-1½, 11}
Jawaban : c
11. Himpunan penyelesaian dari |3t - 2| + |t + 5|=6 adalah...
a. {-9/4, 1/2, 3/4}
b. {-1/2, 3/4, 9/4}
c. {-1/2, 3/4}
d. {1/2, 3/4}
Pembahasan :
Untuk menentukan penyelesaian soal tersebut, gunakan definisi nilai mutlak
|3t - 2|=3t - 2 jika t ≥ 2/3
|3t - 2|=-3t+2 jika t < 2/3 dan
|t + 5|=t + 5 jika t ≥ -5
|t + 5|=-t -5 jika t < -5
dapat dipetakan seperti berikut
Untuk daerah I (hijau)
|3t - 2| + |t + 5|=6
-3t + 2 - t - 5=6
-4t=6 + 5 - 2
-4t=9
t=-9/4 (tidak memenuhi)
Untuk daerah II (coklat)
|3t - 2| + |t + 5|=6
-3t + 2 + t + 5=6
-2t=6 - 2 - 5
-2t= -1
t=1/2 (memenuhi)
Untuk daerah III (pink)
|3t - 2| + |t + 5|=6
3t - 2 + t + 5=6
4t =6 + 2 - 5
4t =3
t =3/4 (memenuhi)
Hp={1/2, 3/4}
Jawaban : d
a. -1/13 dan 5/13
b. -1/13 dan - 5/13
c. -1/13 dan 13/5
d. -1/13 dan -13/5
Pembahasan :
|4p + 7| =3
|3p - 2|
|4p + 7|=3|3p - 2|
4p + 7=3 (3p - 2) atau 4p + 7=3 (-3p + 2)
⇔ 4p + 7=3 (3p - 2)
4p + 7=9p - 6
4p - 9p=- 6 - 7
- 5p=- 13
p=13/5
⇔ 4p + 7=3 (-3p + 2)
4p + 7=-9p + 6
4p + 9p=6 - 7
13p=-1
p=-1/13
Jawaban : c
13. Nilai x yang memenuhi persamaan |2x+5|²+|2x+5| – 6=0 adalah....
a. - 7/2 atau - 3/2
b. - 5/2 atau - 3/2
c. - 3/2 atau 5/2
d. 3/2 atau 7/2
Pembahasan :
misalkan |2x+5|=y, maka
|2x+5|²+|2x+5| – 6=0
⇒ y² + y - 6=0 (faktorkan)
(y + 3) (y - 2)=0
y=-3 atau y=2
|2x+5|=-3 tidak memenuhi karena negatif
|2x+5|=2 memenuhi karena positif, dapat dicari nilai x
2x + 5=2 atau 2x + 5=-2
2x=2 - 5 atau 2x=- 2 - 5
2x=-3 atau 2x=- 7
x=-3/2 atau x=-7/2
Jawaban : a
14. Batas nilai x yang memenuhi pertidaksamaan 3x - 1 > x + 11 adalah....
a. x > -6
b. x < -6
c. x > 6
d. x < 6
Pembahasan :
3x - 1 > x + 11
3x - x > 11 + 1
2x > 12
x > 6
Jawaban : c
15. Himpunan penyelesaian pertidaksamaan 5 - x/6 ≤ 1 adalah....
a. x ≤ 6
b. x ≥ 6
c. x ≤ 24
d. x ≥ 24
Pembahasan :
5 - x/6 ≤ 1 (kalikan dengan 6)
30 - x ≤ 6
- x ≤ 6 - 30
- x ≤ - 24
x ≥ 24 (tanda dibalik karena dibagi angka negatif)
Jawaban : d
a. x ≤ 2/3
b. x ≤ 3/5
c. x ≤ -2
d. x ≤ -5
Pembahasan :
5x + 1 ≤ 2 (kalikan dengan kpk penyebut, yaitu 6)
6 3
5x + 1 ≤ 4
5x ≤ 4 - 1
5x ≤ 3
x ≤ 3/5
Jawaban : b
a. x ≥ 6,3
b. x ≥ 7,2
c. x ≥ 8,1
d. x ≥ 9,0
Pembahasan :
2x + 1 ≥ 4 - x (kalikan dengan kpk penyebut)
9 2 3
4x + 9 ≥ 72 - 6x
4x + 6x ≥ 72 - 9
10x ≥ 63
x ≥ 6,3
Jawaban : a
18. Batas nilai x yang memenuhi x + 5 < 3x - 7 < 2x + 1 adalah...
a. -6 < x < 8
b. 6 < x < 8
c. x < 6 atau x > 8
d. x < -6 atau x > 8
Pembahasan :
x + 5 < 3x - 7 < 2x + 1 berarti
x + 5 < 3x - 7 dan 3x - 7 < 2x + 1
x - 3x < -7 - 5 dan 3x - 2x < 1 + 7
- 2x < - 12 dan x < 8
x > 6 dan x < 8,
⇔ 6 < x < 8
Jawaban : b
19. Himpunan penyelesaian dari |x + 3| < 5 adalah.....
a. {x|-8 < x < -2}
b. {x|-8 < x < 2}
c. {x|-2 < x < 8}
d. {x|2 < x < 8}
Pembahasan:
sifat nilai mutlak
| f(x) | < a ⇔ - a < f(x) < a
|x + 3| < 5
-5 < x + 3 < 5
-5 - 3 < x + 3 - 3 < 5 - 3
-8 < x < 2
Hp={x|-8 < x < 2}
Jawaban : b
20. Himpunan penyelesaian |2x -11| ≥ 3 adalah...
a. x ≥ 7
b. x ≤ 4
c. 4 ≤ x ≤ 7
d. x ≤ 4 atau x ≥ 7
Pembahasan :
sifat nilai mutlak
| f(x) | ≥ a ⇔ f(x) ≥ a atau f(x) ≤ -a
|2x -11| ≥ 3
2x - 11 ≥ 3 atau 2x - 11 ≤ -3
2x ≥ 3 + 11 atau 2x ≤ -3 + 11
2x ≥ 14 atau 2x ≤ 8
x ≥ 7 atau x ≤ 4
Jawaban : d
21. Himpunan penyelesaian 2|3x +17|- 31 ≥ 19 adalah...
a. x ≤ - 14 atau x ≥ 8
b. -14 ≤ x ≤ 8
c. x ≤ - 14 atau x ≥ 8/3
d. -14 ≤ x ≤ 8/3
Pembahasan :
2|3x +17|- 31 ≥ 19
2|3x +17| ≥ 19 + 31
2|3x +17| ≥ 50
|3x +17| ≥ 25, maka
3x + 17 ≥ 25 atau 3x + 17 ≤ - 25
3x ≥ 25 - 17 atau 3x ≤ - 25 - 17
3x ≥ 8 atau 3x ≤ - 42
x ≥ 8/3 atau x ≤ - 14
Jawaban : c
22. Himpunan penyelesaian |3a + 4| ≤ |2a - 5| adalah....
a. {a|-9 ≤ a ≤ 1/5}
b. {a|-1/5 ≤ a ≤ 9}
c. {a|a ≤ -1/5 atau a ≥ 9}
d. {a| a ≤ - 9 atau a ≥ 1/5}
Pembahasan :
sifat nilai mutlak
|f(x)| ≤ |g(x)|
⇔ f²(x) ≤ g²(x)
⇔ f²(x) - g²(x) ≤ 0
⇔ (f(x) + g(x)) (f(x) - g(x)) ≤ 0
|3a + 4| ≤ |2a - 5|
(3a + 4 + 2a - 5) (3a + 4 - 2a + 5) ≤ 0
(5a - 1) (a + 9) ≤ 0
pembuat nol fungsi
5a - 1=0
a=1/5 dan
a + 9=0
a=-9
untuk nilai a ≤ -9, misalkan -10
(5a - 1) (a + 9)=(-10 -1) (-10 + 9)
=(-11) (-1)
=11 (positif)
untuk nilai -9 ≤ a ≤ 1/5, misalkan 0
(5a - 1) (a + 9)=(0 -1) (0 + 9)
=(-1) (9)
=-9 (negatif)
untuk nilai a ≥ 1/5, misalkan 1
(5a - 1) (a + 9)=(5 -1) (1 + 9)
=(4) (10)
=40 positif
jika dipetakan dalam garis bilangan adalah sebagai berikut :
karena tanda ≤ 0, berarti kita mencari nilai yang lebih kecil dari nol atau negatif maka HP={x|-9 ≤ a ≤ 1/5}
Jawaban : a
a. x ≤ -1 atau x ≥ 8
b. x ≤ -8 atau x ≥ 1
a. {-1½, -11}
b. {1½, -11}
c. {-1½, 11}
d. {1½, 11}
Pembahasan :
31− ∣4a−5∣ =20
− ∣4a−5∣ =20 - 31
- |4a-5|=-11
|4a-5|=11
4a - 5=11 atau 4a - 5=-11
⇔ 4a - 5=11
4a =11 + 5
4a =16
a =4
⇔ 4a - 5=-11
4a =-11 + 5
4a =-6
a =-1½
Hp={-1½, 11}
Jawaban : c
11. Himpunan penyelesaian dari |3t - 2| + |t + 5|=6 adalah...
a. {-9/4, 1/2, 3/4}
b. {-1/2, 3/4, 9/4}
c. {-1/2, 3/4}
d. {1/2, 3/4}
Pembahasan :
Untuk menentukan penyelesaian soal tersebut, gunakan definisi nilai mutlak
|3t - 2|=3t - 2 jika t ≥ 2/3
|3t - 2|=-3t+2 jika t < 2/3 dan
|t + 5|=t + 5 jika t ≥ -5
|t + 5|=-t -5 jika t < -5
dapat dipetakan seperti berikut
|3t - 2| + |t + 5|=6
-3t + 2 - t - 5=6
-4t=6 + 5 - 2
-4t=9
t=-9/4 (tidak memenuhi)
Untuk daerah II (coklat)
|3t - 2| + |t + 5|=6
-3t + 2 + t + 5=6
-2t=6 - 2 - 5
-2t= -1
t=1/2 (memenuhi)
Untuk daerah III (pink)
|3t - 2| + |t + 5|=6
3t - 2 + t + 5=6
4t =6 + 2 - 5
4t =3
t =3/4 (memenuhi)
Hp={1/2, 3/4}
Jawaban : d
a. -1/13 dan 5/13
b. -1/13 dan - 5/13
c. -1/13 dan 13/5
d. -1/13 dan -13/5
Pembahasan :
|4p + 7| =3
|3p - 2|
|4p + 7|=3|3p - 2|
4p + 7=3 (3p - 2) atau 4p + 7=3 (-3p + 2)
⇔ 4p + 7=3 (3p - 2)
4p + 7=9p - 6
4p - 9p=- 6 - 7
- 5p=- 13
p=13/5
⇔ 4p + 7=3 (-3p + 2)
4p + 7=-9p + 6
4p + 9p=6 - 7
13p=-1
p=-1/13
Jawaban : c
13. Nilai x yang memenuhi persamaan |2x+5|²+|2x+5| – 6=0 adalah....
a. - 7/2 atau - 3/2
b. - 5/2 atau - 3/2
c. - 3/2 atau 5/2
d. 3/2 atau 7/2
Pembahasan :
misalkan |2x+5|=y, maka
|2x+5|²+|2x+5| – 6=0
⇒ y² + y - 6=0 (faktorkan)
(y + 3) (y - 2)=0
y=-3 atau y=2
|2x+5|=-3 tidak memenuhi karena negatif
|2x+5|=2 memenuhi karena positif, dapat dicari nilai x
2x + 5=2 atau 2x + 5=-2
2x=2 - 5 atau 2x=- 2 - 5
2x=-3 atau 2x=- 7
x=-3/2 atau x=-7/2
Jawaban : a
14. Batas nilai x yang memenuhi pertidaksamaan 3x - 1 > x + 11 adalah....
a. x > -6
b. x < -6
c. x > 6
d. x < 6
Pembahasan :
3x - 1 > x + 11
3x - x > 11 + 1
2x > 12
x > 6
Jawaban : c
15. Himpunan penyelesaian pertidaksamaan 5 - x/6 ≤ 1 adalah....
a. x ≤ 6
b. x ≥ 6
c. x ≤ 24
d. x ≥ 24
Pembahasan :
5 - x/6 ≤ 1 (kalikan dengan 6)
30 - x ≤ 6
- x ≤ 6 - 30
- x ≤ - 24
x ≥ 24 (tanda dibalik karena dibagi angka negatif)
Jawaban : d
a. x ≤ 2/3
b. x ≤ 3/5
c. x ≤ -2
d. x ≤ -5
Pembahasan :
5x + 1 ≤ 2 (kalikan dengan kpk penyebut, yaitu 6)
6 3
5x + 1 ≤ 4
5x ≤ 4 - 1
5x ≤ 3
x ≤ 3/5
Jawaban : b
a. x ≥ 6,3
b. x ≥ 7,2
c. x ≥ 8,1
d. x ≥ 9,0
Pembahasan :
2x + 1 ≥ 4 - x (kalikan dengan kpk penyebut)
9 2 3
4x + 9 ≥ 72 - 6x
4x + 6x ≥ 72 - 9
10x ≥ 63
x ≥ 6,3
Jawaban : a
18. Batas nilai x yang memenuhi x + 5 < 3x - 7 < 2x + 1 adalah...
a. -6 < x < 8
b. 6 < x < 8
c. x < 6 atau x > 8
d. x < -6 atau x > 8
Pembahasan :
x + 5 < 3x - 7 < 2x + 1 berarti
x + 5 < 3x - 7 dan 3x - 7 < 2x + 1
x - 3x < -7 - 5 dan 3x - 2x < 1 + 7
- 2x < - 12 dan x < 8
x > 6 dan x < 8,
⇔ 6 < x < 8
Jawaban : b
19. Himpunan penyelesaian dari |x + 3| < 5 adalah.....
a. {x|-8 < x < -2}
b. {x|-8 < x < 2}
c. {x|-2 < x < 8}
d. {x|2 < x < 8}
Pembahasan:
sifat nilai mutlak
| f(x) | < a ⇔ - a < f(x) < a
|x + 3| < 5
-5 < x + 3 < 5
-5 - 3 < x + 3 - 3 < 5 - 3
-8 < x < 2
Hp={x|-8 < x < 2}
Jawaban : b
20. Himpunan penyelesaian |2x -11| ≥ 3 adalah...
a. x ≥ 7
b. x ≤ 4
c. 4 ≤ x ≤ 7
d. x ≤ 4 atau x ≥ 7
Pembahasan :
sifat nilai mutlak
| f(x) | ≥ a ⇔ f(x) ≥ a atau f(x) ≤ -a
|2x -11| ≥ 3
2x - 11 ≥ 3 atau 2x - 11 ≤ -3
2x ≥ 3 + 11 atau 2x ≤ -3 + 11
2x ≥ 14 atau 2x ≤ 8
x ≥ 7 atau x ≤ 4
Jawaban : d
21. Himpunan penyelesaian 2|3x +17|- 31 ≥ 19 adalah...
a. x ≤ - 14 atau x ≥ 8
b. -14 ≤ x ≤ 8
c. x ≤ - 14 atau x ≥ 8/3
d. -14 ≤ x ≤ 8/3
Pembahasan :
2|3x +17|- 31 ≥ 19
2|3x +17| ≥ 19 + 31
2|3x +17| ≥ 50
|3x +17| ≥ 25, maka
3x + 17 ≥ 25 atau 3x + 17 ≤ - 25
3x ≥ 25 - 17 atau 3x ≤ - 25 - 17
3x ≥ 8 atau 3x ≤ - 42
x ≥ 8/3 atau x ≤ - 14
Jawaban : c
22. Himpunan penyelesaian |3a + 4| ≤ |2a - 5| adalah....
a. {a|-9 ≤ a ≤ 1/5}
b. {a|-1/5 ≤ a ≤ 9}
c. {a|a ≤ -1/5 atau a ≥ 9}
d. {a| a ≤ - 9 atau a ≥ 1/5}
Pembahasan :
sifat nilai mutlak
|f(x)| ≤ |g(x)|
⇔ f²(x) ≤ g²(x)
⇔ f²(x) - g²(x) ≤ 0
⇔ (f(x) + g(x)) (f(x) - g(x)) ≤ 0
|3a + 4| ≤ |2a - 5|
(3a + 4 + 2a - 5) (3a + 4 - 2a + 5) ≤ 0
(5a - 1) (a + 9) ≤ 0
pembuat nol fungsi
5a - 1=0
a=1/5 dan
a + 9=0
a=-9
untuk nilai a ≤ -9, misalkan -10
(5a - 1) (a + 9)=(-10 -1) (-10 + 9)
=(-11) (-1)
=11 (positif)
untuk nilai -9 ≤ a ≤ 1/5, misalkan 0
(5a - 1) (a + 9)=(0 -1) (0 + 9)
=(-1) (9)
=-9 (negatif)
untuk nilai a ≥ 1/5, misalkan 1
(5a - 1) (a + 9)=(5 -1) (1 + 9)
=(4) (10)
=40 positif
jika dipetakan dalam garis bilangan adalah sebagai berikut :
karena tanda ≤ 0, berarti kita mencari nilai yang lebih kecil dari nol atau negatif maka HP={x|-9 ≤ a ≤ 1/5}
Jawaban : a
a. x ≤ -1 atau x ≥ 8
b. x ≤ -8 atau x ≥ 1
c. -1 ≤ x ≤ 8, x ≠ 2
d. 1 ≤ x ≤ 8, x ≠ 2
Pembahasan :
|x + 10| ≥ 3
| x - 2|
|x + 10| ≥ 3 |x-2|
(x+10)² - 9(x-2)² ≥ 0
(x+10 + 3(x-2)) (x+10 - 3(x-2)) ≥ 0
(4x + 4) (-2x + 16) ≥ 0
pembuat nol fungsi
4x + 4=0 dan -2x + 16=0
x=-1 dan x=8
Untuk x ≤ -1, misalkan -2
(4x + 4) (-2x + 16)=(4(-2) + 4) (-2(-2) + 16)
=(-4) (20)
=- 80 (negatif)
untuk -1 ≤ x ≤ 8, misalkan 0
=(-4) (20)
=- 80 (negatif)
untuk -1 ≤ x ≤ 8, misalkan 0
(4x + 4) (-2x + 16)=(4(0) + 4) (-2(0) + 16)
=(4) (16)
=64 (positif)
untuk x ≥ 8, misalkan 9
=(4) (16)
=64 (positif)
untuk x ≥ 8, misalkan 9
(4x + 4) (-2x + 16)=(4(9) + 4) (-2(9) + 16)
=(40) (-2)
=- 80 (negatif)
(4x + 4) (-2x + 16) ≥ 0
24. Himpunan penyelesaian dari pertidaksamaan 1 < |x- 7| < 5 adalah....
a. {x | 2 < x < 6}
b. {x | 8 < x < 12}
c. {x | 1 < x < 5}
d.{x | 2 < x < 6 atau 8 < x < 12}
Pembahasan :
1 < |x - 7| < 5
bentuk ini dipecah menjadi
1 < |x - 7| dan |x - 7| < 5
⇔ 1 < |x - 7| ⇔ |x - 7| > 1
x - 7 > 1 atau x - 7 < -1
x > 1 + 7 atau x < -1 + 7
x > 8 atau x < 6
⇔ |x - 7| < 5
- 5 < x - 7 < 5
-5 + 7 < x - 7 + 7 < 5 + 7
2 < x < 12
Perhatikan garis bilangan berikut untuk melihat irisan jawaban
Daerah yang diarsir adalah irisan jawaban
Hp={x | 2 < x < 6 atau 8 < x < 12}
Jawaban : d
25. Himpunan penyelesaian dari pertidaksamaan |x - 6| + |x + 4| ≥ 4 adalah.....
a. {x | x ≤ -1 atau x ≥ 3}
b.{x | -1 ≤ x ≤ 3}
c.{x | x < -4 atau x ≥ 6}
d.{x | -4 < x ≤ 6}
Pembahasan :
Dengan menggunakan definisi nilai mutlak
|x - 6| ⇔ x - 6, jika x ≥ 6
⇔-x + 6, jika x < 6
|x + 4|⇔ x + 4, jika x ≥ -4
⇔ -x - 4, jika x < -4
dipetakan pada garis bilangan sebagai berikut
|x - 6| + |x + 4| ≥ 4
-x + 6 - x - 4 ≥ 4
-x - x ≥ 4 - 6 + 4
- 2x ≥ 2
x ≤ -1
Irisan dari x < -4 dan x ≤ -1 adalah x < -4
Untuk daerah II (pink)
|x - 6| + |x + 4| ≥ 4
-x + 6 + x + 4 ≥ 4
-x + x ≥ 4 - 6 - 4
0 ≥ - 6
bukan penyelesaian
Untuk daerah III (hijau)
|x - 6| + |x + 4| ≥ 4
x - 6 + x + 4 ≥ 4
x + x ≥ 4 + 6 - 4
2x ≥ 6
x ≥ 3
Irisan dari x ≥ 6 dan x ≥ 3 adalah x ≥ 6
maka HP={x | x < -4 atau x ≥ 6}
Jawaban : c
=(40) (-2)
=- 80 (negatif)
(4x + 4) (-2x + 16) ≥ 0
karena nilai yang diinginkan adalah ≥ 0, maka x yang memenuhi adalah yang menghasilkan nilai positif yaitu -1 ≤ x ≤ 8 dan x ≠ 2 karena x - 2 ≠ 0
Jawaban : c
24. Himpunan penyelesaian dari pertidaksamaan 1 < |x- 7| < 5 adalah....
a. {x | 2 < x < 6}
b. {x | 8 < x < 12}
c. {x | 1 < x < 5}
d.{x | 2 < x < 6 atau 8 < x < 12}
Pembahasan :
1 < |x - 7| < 5
bentuk ini dipecah menjadi
1 < |x - 7| dan |x - 7| < 5
⇔ 1 < |x - 7| ⇔ |x - 7| > 1
x - 7 > 1 atau x - 7 < -1
x > 1 + 7 atau x < -1 + 7
x > 8 atau x < 6
⇔ |x - 7| < 5
- 5 < x - 7 < 5
-5 + 7 < x - 7 + 7 < 5 + 7
2 < x < 12
Perhatikan garis bilangan berikut untuk melihat irisan jawaban
Daerah yang diarsir adalah irisan jawaban
Hp={x | 2 < x < 6 atau 8 < x < 12}
Jawaban : d
25. Himpunan penyelesaian dari pertidaksamaan |x - 6| + |x + 4| ≥ 4 adalah.....
a. {x | x ≤ -1 atau x ≥ 3}
b.{x | -1 ≤ x ≤ 3}
c.{x | x < -4 atau x ≥ 6}
d.{x | -4 < x ≤ 6}
Pembahasan :
Dengan menggunakan definisi nilai mutlak
|x - 6| ⇔ x - 6, jika x ≥ 6
⇔-x + 6, jika x < 6
|x + 4|⇔ x + 4, jika x ≥ -4
⇔ -x - 4, jika x < -4
dipetakan pada garis bilangan sebagai berikut
|x - 6| + |x + 4| ≥ 4
-x + 6 - x - 4 ≥ 4
-x - x ≥ 4 - 6 + 4
- 2x ≥ 2
x ≤ -1
Irisan dari x < -4 dan x ≤ -1 adalah x < -4
Untuk daerah II (pink)
|x - 6| + |x + 4| ≥ 4
-x + 6 + x + 4 ≥ 4
-x + x ≥ 4 - 6 - 4
0 ≥ - 6
bukan penyelesaian
Untuk daerah III (hijau)
|x - 6| + |x + 4| ≥ 4
x - 6 + x + 4 ≥ 4
x + x ≥ 4 + 6 - 4
2x ≥ 6
x ≥ 3
Irisan dari x ≥ 6 dan x ≥ 3 adalah x ≥ 6
maka HP={x | x < -4 atau x ≥ 6}
Jawaban : c