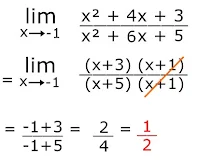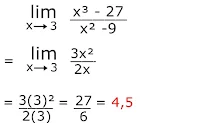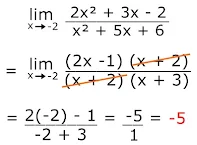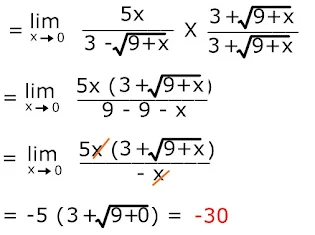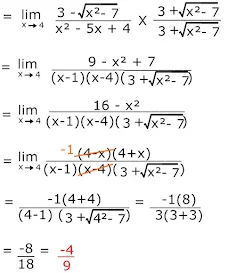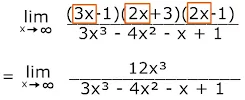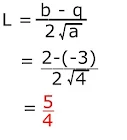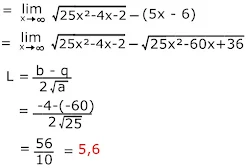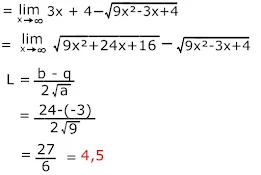Soal Limit Fungsi Aljabar By Bimbel Jakarta Timur
 |
| Soal Limit Fungsi Aljabar Bimbel Jakarta Timur |
Sebelum lebih jauh mari kita bahas pengertian Limit Fungsi yaitu suatu konsep matematika tentang perilaku suatu fungsi yang mendekati suatu titik masukan tertentu.
Penyelesaian persamaan dan kumpulan persamaan adalah bagian penting dan penting secara historis dari apa yang kita sebut Aljabar. Aljabar umumnya digunakan dalam rumus ketika kita dapat mengubah salah satu angka atau setidaknya salah satu angka tidak diketahui. Pada soal latihan ini, kita akan mempelajari aljabar limit.
Metode aljabar digunakan untuk menghitung limit. Beberapa metode penting adalah metode faktorisasi, evaluasi menggunakan batas baku, metode substitusi langsung, rasionalisasi dan evaluasi batas tak terhingga.
Untuk mencari limit suatu fungsi secara aljabar, ada empat teknik untuk dipilih: memasukkan nilai x, memfaktorkan, merasionalkan pembilangnya, dan menemukan penyebut persekutuan terkecil.
Tempat terbaik untuk memulai adalah teknik pertama. Kita hanya dapat menggunakan teknik ini jika fungsinya kontinu pada nilai x yang kita ambil limitnya. Jika fungsi tidak terdefinisi pada nilai x ini, Kita harus beralih ke teknik lain untuk menyederhanakan fungsi sehingga dapat memasukkan nilai x yang mendekati.
Selanjutnya mari berlatih dalam soal limit fungsi aljabar ini:
adalah....a. 2
b. 3
c. 6
d. 9
Pembahasan :
Teorama limit
maka nilai limit=62. Nilai dari
adalah....a. -6
b. -3
c. 2
d. 6
Pembahasan :
Teorama limit
maka nilai limit adalah
L=-3(2)=-6
3. Nilai dari
adalah.... a. -5
b. 4
c. 5
d. 11
Pembahasan :
L=4² - 5
=16 - 5=11
4. Nilai dari
adalah....a. -1/2
b. 1/2
c. 3/4
d. 3/5
Pembahasan :
Jika bilangan -1 disubstitusi ke dalam fungsi akan menghasilkan bentuk
, maka fungsi harus difaktorkan dan menghilangkan bentuk yang sama.
5. Nilai dari
adalah.... a. -32
b. -8
c. 2
d. 4
Pembahasan :
Jika bilangan 4 disubstitusi ke dalam fungsi akan menghasilkan bentuk
, maka fungsi harus difaktorkan dan menghilangkan bentuk yang sama.
6. Nilai dari
adalah....
a. -3
b. 3
c. 4,5
d. 9
Pembahasan :
Cara pemfaktoran ini adalah cara yang umum dilakukan dengan asumsi kamu mempelajari materi limit sebelum materi diferensial/turunan. Jika kamu sudah mempelajari materi turunan, kamu bisa menyelesaikan soal ini dengan dalil L'hopital atau cara turunan.
Turunkan masing-masing fungsi pembilang dan penyebut, setelah itu kamu dapat substitusi nilai batas limit.
cara turunan
7. Nilai dari
adalah.....
a. -4
b. 0
c. 3
d. 4
Pembahasan :
Rasionalkan penyebut
8. Nilai dari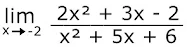
adalah....
a. -5
b. -1/3
c. 3
d. 5
Pembahasan :
cara pemfaktoran
cara turunan (L'hopital)
9. Nilai dari
adalah....
a. -1
b. 1/9
c. 1/3
d. 3
Pembahasan :
10. Nilai dari
adalah...
a. -1
b. 1
c. 2
d. 4
Pembahasan :
11. Nilai dari
adalah.....
a. -1/3
b. -1/6
c. 1/3
d. 4
Pembahasan :
Bentuk limit ini diselesaikan dengan perkalian sekawan
12. Nilai dari
adalah....
a.
Pembahasan :
13. Nilai dari
adalah.....
a. -30
b. -5
c. 5
d. 6
Pembahasan :
14. Nilai dari
6. Nilai dari
adalah.... a. -3
b. 3
c. 4,5
d. 9
Pembahasan :
Cara pemfaktoran ini adalah cara yang umum dilakukan dengan asumsi kamu mempelajari materi limit sebelum materi diferensial/turunan. Jika kamu sudah mempelajari materi turunan, kamu bisa menyelesaikan soal ini dengan dalil L'hopital atau cara turunan.
Turunkan masing-masing fungsi pembilang dan penyebut, setelah itu kamu dapat substitusi nilai batas limit.
cara turunan
7. Nilai dari
adalah.....a. -4
b. 0
c. 3
d. 4
Pembahasan :
Rasionalkan penyebut
8. Nilai dari
adalah....a. -5
b. -1/3
c. 3
d. 5
Pembahasan :
cara pemfaktoran
cara turunan (L'hopital)
9. Nilai dari
adalah....a. -1
b. 1/9
c. 1/3
d. 3
Pembahasan :
10. Nilai dari
adalah...a. -1
b. 1
c. 2
d. 4
Pembahasan :
11. Nilai dari
adalah.....a. -1/3
b. -1/6
c. 1/3
d. 4
Pembahasan :
Bentuk limit ini diselesaikan dengan perkalian sekawan
12. Nilai dari
adalah....a.
Pembahasan :
13. Nilai dari
adalah.....a. -30
b. -5
c. 5
d. 6
Pembahasan :
14. Nilai dari
adalah.....
a. -9
b. -7
c. 9
d. 16
Pembahasan :
15. Nilai dari
21. Nilai dari
adalah....
a. 0
b. 2
c. 4
d. ∞
Pembahasan :
a=koefisien suku pertama=4
p= koefisien suku kedua=4
karena a=p, maka nilai limit=0
22. Nilai dari
adalah....
a. 1/3
b. 2/3
c. 2/9
d. 4
Pembahasan :
Jika a > p, maka nilai limit=∞
Jika a=p, maka nilai limit=
Jika a < p, maka nilai limit=- ∞
a=9, b=6, c=4
p=9, q=2
karena a=p, maka
23. Nilai dari
adalah....
a. 5/8
b. 5/4
c. -1/8
d. -1/4
Pembahasan :
a=4, b=2
p=4, q=-3
24. Nilai dari
adalah....
a. -6,4
b. -5,6
c. 5,6
d. 6,4
Pembahasan :
25. Nilai dari
adalah....
a. 2,5
b. 3,5
c. 4,5
d. 7,5
Pembahasan :
a. -9
b. -7
c. 9
d. 16
Pembahasan :
15. Nilai dari
adalah.....
a. -4
b. -4/9
c. 4
d. 9
Pembahasan :
16. Nilai dari
adalah.....
a. 0
b. 2
c. 4
d. ∞
Pembahasan :
Limit Tak Hingga
Jika n < m, makanilai limit=0
Jika n=m, maka nilailimit=a/p
Jika n > m, makanilai limit=∞
n=pangkat tertinggi pembilang=4
m=pangkat tertinggi penyebut=4
a=koefisien suku pembilang dengan pangkat tertinggi=8
p= koefisien suku penyebut dengan pangkat tertinggi=2
n=m, maka nilai limit=a/p=8/2=4
17. Nilai dari
adalah....
a. 0
b. 2
c. 4
d. ∞
Pembahasan :
karena yang dibutuhkan hanya pangkat x tertinggi, cukup kalikan suku-suku yang mengandung x sehingga didapatkan
n=3, m=3
a=12, p=3
karena n=m, maka L=a/p=12/3=4
18. Nilai dari
adalah.....
a. 0
b. 3
c. 6
d. ∞
Pembahasan :
pembilang 6x⁶
penyebut (3x³)(x²)=3x⁵
n=6, m=5
Jika n > m, maka nilai limit= ∞
19. Nilai dari
adalah....
a. 0
b. -1
c. 1
d. ∞
Pembahasan :
Pembilang=√x²=x
Penyebut=x²
n=1, m=2
karena n < m, maka nilai limit=0
20. Nilai dari
adalah...
a. 0
b. 2
c. 3
d. ∞
Pembahasan :
Jikaa > p, maka nilai limit=∞
Jikaa=p, maka nilai limit=0
Jika a< p, maka nilai limit=- ∞
a=koefisien suku pertama=3
p= koefisien suku kedua=1
karena a > p, maka nilai limit=∞
a. -4
b. -4/9
c. 4
d. 9
Pembahasan :
16. Nilai dari
adalah.....a. 0
b. 2
c. 4
d. ∞
Pembahasan :
Limit Tak Hingga
Jika n < m, makanilai limit=0
Jika n=m, maka nilailimit=a/p
Jika n > m, makanilai limit=∞
n=pangkat tertinggi pembilang=4
m=pangkat tertinggi penyebut=4
a=koefisien suku pembilang dengan pangkat tertinggi=8
p= koefisien suku penyebut dengan pangkat tertinggi=2
n=m, maka nilai limit=a/p=8/2=4
17. Nilai dari
adalah....a. 0
b. 2
c. 4
d. ∞
Pembahasan :
karena yang dibutuhkan hanya pangkat x tertinggi, cukup kalikan suku-suku yang mengandung x sehingga didapatkan
n=3, m=3
a=12, p=3
karena n=m, maka L=a/p=12/3=4
18. Nilai dari
adalah.....a. 0
b. 3
c. 6
d. ∞
Pembahasan :
pembilang 6x⁶
penyebut (3x³)(x²)=3x⁵
n=6, m=5
Jika n > m, maka nilai limit= ∞
19. Nilai dari
adalah....a. 0
b. -1
c. 1
d. ∞
Pembahasan :
Pembilang=√x²=x
Penyebut=x²
n=1, m=2
karena n < m, maka nilai limit=0
20. Nilai dari
adalah...a. 0
b. 2
c. 3
d. ∞
Pembahasan :
Jikaa > p, maka nilai limit=∞
Jikaa=p, maka nilai limit=0
Jika a< p, maka nilai limit=- ∞
a=koefisien suku pertama=3
p= koefisien suku kedua=1
karena a > p, maka nilai limit=∞
21. Nilai dari
adalah....a. 0
b. 2
c. 4
d. ∞
Pembahasan :
a=koefisien suku pertama=4
p= koefisien suku kedua=4
karena a=p, maka nilai limit=0
22. Nilai dari
adalah....a. 1/3
b. 2/3
c. 2/9
d. 4
Pembahasan :
Jika a > p, maka nilai limit=∞
Jika a=p, maka nilai limit=
Jika a < p, maka nilai limit=- ∞
a=9, b=6, c=4
p=9, q=2
karena a=p, maka
23. Nilai dari
adalah....a. 5/8
b. 5/4
c. -1/8
d. -1/4
Pembahasan :
a=4, b=2
p=4, q=-3
24. Nilai dari
adalah....a. -6,4
b. -5,6
c. 5,6
d. 6,4
Pembahasan :
25. Nilai dari
adalah....a. 2,5
b. 3,5
c. 4,5
d. 7,5
Pembahasan :
SEMOGA BERMANFAAT
0 Komentar: