Himpunan yaitu kelompok, kumpulan benda atau objek yang memiliki definisi maupun ukuran pasti sehingga anggotanya dapat disebut dengan jelas.
Teori himpunan adalah cabang logika matematika yang mempelajari himpunan, yang secara informal dapat digambarkan sebagai kumpulan objek. Meskipun objek dalam bentuk apa pun dapat dikumpulkan menjadi satu himpunan,
1. Perhatikan kumpulan-kumpulan berikut:
I. kumpulan siswa yang cerdas
II. kumpulan hewan mamalia
III. kumpulan hewan yang lucu
IV. kumpulan huruf vokal
Yang merupakan himpunan adalah...
a. I dan III
b. II dan IV
c. I, II dan III
d. IV saja
Pembahasan :
Kumpulan dapat disebut himpunan jika anggotanya dapat disebutkan dengan jelas. Cirinya adalah tidak menggunakan kata sifat yang acuan ukurannya bisa berbeda.
I. bukan himpunan karena cerdas adalah kata sifat
II. termasuk himpunan karena hewan mamalia dapat disebutkan
III. bukan himpunan karena lucu adalah kata sifat
IV. himpunan karena dapat disebutkan
2. A={10 bilangan prima pertama}
Pernyataan berikut yang tidak benar adalah...
a. 7 ∈ A
b. 29 ∈ A
c. 19 ∉ A
d. 15 ∉ A
Pembahasan :
A jika ditulis dengan mendaftar anggota-anggotanya
={2, 3, 5, 7, 11, 13, 17, 19, 23, 29}
7 ∈ A dibaca "7 anggota himpunan A" (benar)
29 ∈ A dibaca "29 anggota himpunan A" (benar)
19 ∉ A dibaca "19 bukan anggota himpunan A" (salah)
15 ∉ A "15 bukan anggota himpunan A" (benar)
3. B={1, 3, 5, ..., 15}
C={x| x < 9, x ∈ himpunan bilangan cacah}
Pernyataan berikut yang benar adalah....
a. n(B)=15
b. n(C)=8
c. n(B)=8
d. n (D)=10
Pembahasan :
B={1, 3, 5, 7, 9, 11, 13,15}(bilangan ganjil)
n(B)=jumlah anggota himpunan B=8
C={0, 1, 2, 3, 4, 5, 6, 7, 8}
n(C)=9
4. Himpunan berikut yang sama dengan{5, 7, 11, 13, 17, 19}adalah....
a.{x| 3 < x < 20, x ∈ himpunan bilangan prima}
b. {x| 5 ≤ x ≤ 19, x ∈ himpunan bilangan ganjil}
c.{6 bilangan prima yang pertama}
d.{bilangan ganjil antara 4 dan 20}
Pembahasan :
a. {5, 7, 11, 13, 15, 17, 19}
b.{5, 7, 9, 11, 13, 15, 17, 19}
c.{2, 3, 5, 7, 11, 13}
d.{5, 7, 9, 11, 13, 15, 17, 19}
5. Perhatikan himpunan-himpunan berikut :
K={bilangan ganjil yang habis dibagi 2}
L={bilangan prima genap}
M={x| 10 < x < 15, x ∈ himpunan bilangan kuadrat}
Yang merupakan himpunan kosong adalah...
a. K, L dan M
b. K dan L
c. K dan M
d. L dan M
Pembahasan :
K={}
L={2}
M={}
6. Jika A={3, 5, 7, 9, 11}, maka yang tidak dapat menjadi himpunan semesta dari A adalah....
a.{bilangan asli}
b.{bilangan bulat}
c.{bilangan ganjil}
d.{bilangan prima}
Pembahasan :
Semua anggota himpunan A adalah bilangan asli, bulat dan ganjil, sedangkan 9 bukan bilangan prima.
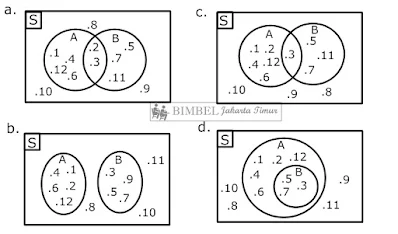
7. Diketahui :
S={x| x < 13, x ∈ himpunan bilangan asli}
A={faktor dari 12}
B={{x| x < 13, x ∈ himpunan bilangan prima}
Diagram Venn untuk himpunan-himpunan di atas adalah...
Pembahasan :
S={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
A={1, 2, 3, 4, 6, 12}
B={2, 3, 5, 7, 11}
A dan B merupakan dua himpunan yang tidak saling lepas karena memiliki anggota yang sama yaitu 2 dan 3. Diagram Venn yang sesuai digambarkan pilihan a.
8. Diketahui
S={bilangan bulat}
P={bilangan asli}
Q={bilangan kuadrat}
Diagram Venn untuk himpunan-himpunan di atas yang benar adalah...
Pembahasan :
Semua bilangan kuadrat merupakan bilangan asli tetapi tidak semua bilangan asli merupakan bilangan kuadrat. Maka himpunan Q merupakan himpunan bagian dari P. Digambarkan pada diagram Venn d.
9. Diketahui :
K={k, e, j, o, r, a}
L={j, e, r, o}
M={k, e, r, a}
Pernyataan yang benar adalah...
a. K ⊂ L
b. K ⊂ M
c. L ⊂ M
d. L ⊂ K
Pembahasan :
Semua anggota L merupakan anggota K, maka L ⊂ K
10. Diketahui A={faktor dari 18}. Banyaknya himpunan bagian dari A adalah...
a. 6
b. 16
c. 32
d. 64
Pembahasan :
A={1, 2, 3, 6, 9, 18}
n(A)=6
Banyaknya himpunan bagian A=2⁶=64
11. Diketahui P={huruf vokal}. Banyaknya himpunan bagian P yang memiliki 3 anggota adalah...
a. 5
b. 6
c. 10
d. 15
Pembahasan :
P={a, i, u, e, o}
Himpunan bagian P yang memiliki 3 anggota
cara I mendaftar semua himpunan yang mungkin
{a, i, u},{a, i, e},{a, i, o},{a, u, e},{a, u, o},{a, e, o},{i, u, e},{i, u, o},{i, e, o},{u, e, o}=10
cara II menggunakan segitiga Pascal
12. Diketahui :
A={bilangan cacah}
B={bilangan genap}
C={bilangan prima}
D={bilangan ganjil}
Pasangan himpunan yang saling lepas adalah...
a. A dan B
b. B dan D
c. C dan D
d. B dan C
Pembahasan :
Dua himpunan disebut saling lepas jika tidak memiliki anggota yang sama.
B={bilangan genap}dan D={bilangan ganjil}tidak memiliki anggota yang sama, maka B dan D saling lepas
13. Jika M={warna lampu lalulintas}, maka himpunan di bawah ini yang ekuivalen dengan M adalah....
a.{faktor ganjil dari 15}
b.{bilangan prima kurang dari 7}
c.{warna pelangi}
d.{faktor prima dari 48}
Pembahasan :
Himpunan ekuivalen adalah dua himpunan yang memiliki jumlah anggota himpunan yang sama
M={merah, kuning, hijau}, n(M)=3
{faktor ganjil dari 15}={1, 3, 5, 15}, n=4
{bilangan prima kurang dari 7}={2, 3, 5}, n=3
{warna pelangi}={merah, jingga, kuning, hijau, biru, nila, ungu}, n=7
{faktor prima dari 48}={2, 3}, n=2
14. Jika S={bilangan cacah kurang dari 10}dan B={faktor prima dari 84}, maka Bc adalah....
a.{0, 1, 4, 5, 6, 8, 9}
b.{1, 4, 5, 6, 8, 9}
c. {0, 1, 2, 4, 6, 8, 9}
d.{5, 8, 9}
Pembahasan :
S={0, 1, 2, 3, 4 5, 6, 7, 8, 9}
B={2, 3, 7}
Bc =komplemen dari himpunan B=yang bukan anggota himpunan B
={0, 1, 4, 5, 6, 8, 9}
15. Jika M={faktor dari 20}dan N={x| 4 ≤ x < 12, x ∈ bilangan genap}, maka M - N=
a.{1, 2, 4, 5, 20}
b.{1, 2, 5, 20}
c.{1, 2, 5, 6, 8}
d.{1, 2, 4, 20}
Pembahasan :
M={1, 2, 4, 5, 10, 20}
N={4, 6, 8, 10}
M - N={1, 2, 5, 20}
16. Diagram Venn yang menunjukkan A ∩ B adalah....
Pembahasan :
A ∩ B=irisan himpunan A dan B
=anggota himpunan A yang juga merupakan anggota himpunan B (diagram c)
17. Jika P={faktor dari 20}dan Q={faktor dari 30}, maka P U Q adalah...
a.{2, 5}
b.{1, 2, 5, 10}
c.{1, 2, 3, 4, 5, 6, 10, 15}
d.{1, 2, 3, 4, 5, 6, 10, 15, 20, 30}
Pembahasan :
P={1, 2, 4, 5, 10, 20}
Q={1, 2, 3, 5, 6, 10, 15, 30}
P U Q=gabungan himpunan P dan Q
=semua anggota himpunan P maupun Q
= {1, 2, 3, 4, 5, 6, 10, 15, 20, 30}
18. Diketahui n(A)=25, n(B)=22 dan n(A ∩ B)=14, maka n(AUB)=...
a. 19
b. 33
c. 40
d. 63
Pembahasan :
RUMUS
n(AUB)=n(A) + n(B) - n(A⋂B)
n(AUB)=25 + 22 - 14
=33
19. Diketahui n(A)=21, n(B)=17. Jika B ⊂ A, maka n(A ∩ B)=....
a. 4
b. 17
c. 21
d. 38
Pembahasan :
Jika B ⊂ A, maka semua anggota B juga merupakan anggota A sehingga
n(A ∩ B)=n(B)=17
20. Perhatikan diagram Venn berikut
Notasi yang tepat untuk daerah yang diarsir adalah...
a. (A ∩ B) U C
b. A ∩ (B U C)
c. (A U B) ∩ C
d. (A U B) U C
Pembahasan :
Gabungan dari himpunan A dan B yang sama dengan himpunan C= (A U B) ∩ C
21. Siswa laki-laki kelas 7A ditanya tentang olahraga kesukaan mereka. 18 orang suka futsal, 16 suka bola basket dan 11 orang menyukai keduanya. Berapa jumlah siswa laki-laki dalam kelas tersebut?
a. 23 orang
b. 24 orang
c. 33 orang
d. 34 orang
Pembahasan :
n(futsal)=n(F)=18
n(basket)=n(B)=16
n(F ⋂ B)=11
n(F U B)= n(F) + n(B) - n(F ⋂ B)
=18 + 16 - 11=23
22. Siswa kelas 7B berjumlah 45 orang. Mereka ditanyai tentang pelajaran kesukaan mereka. Ada 27 orang yang menjawab suka matematika sedangkan yang menyukai IPA ada 23 orang. Jika diantaranya ada 12 yang menyukai matematika maupun IPA, maka diagram venn yang tepat untuk keadaan tersebut adalah...
Pembahasan :
S=45
n(matematika)=n(M)=27
n(IPA)=n(I)=23
n(M ∩ I)=12
Yang hanya menyukai matematika=27 - 12=15
Yang hanya menyukai IPA=23 - 12=11
Yang tidak menyukai matematika maupun IPA=45 - (15 + 11 + 12)=7
Diagram venn yang tepat adalah d
23. Sebanyak 68 ibu rumahtangga di suatu kelurahan disurvei tentang acara hiburan kesukaan mereka. Sebanyak 26 orang suka menonton sinetron, 34 suka drama Korea dan 19 orang tidak menyukai keduanya. Berapa jumlah ibu rumahtangga yang suka menonton sinetron maupun drama Korea?
a. 9 orang
b. 10 orang
c. 11 orang
d. 12 orang
Pembahasan :
S=68
n(S)=26
n(D)=34
n(S U D)'=19
n(S ∩ D)=?
Jumlah ibu rumahtangga yang menyukai sinetron atau drama Korea
n(S U D)=S - n(S U D)'
=68 - 19=49 orang
n(S U D)=n(S) + n(D) - n(S ∩ D)
47 =26 + 34 - x
x =60 - 49
=11 orang
24. Pak Guru mendaftar peserta lomba untuk 40 orang siswanya. Sebanyak 27 siswa mendaftar untuk ikut lomba pidato dan 24 orang ikut lomba MTQ. Jika ada 7 orang siswa yang tidak ingin ikut lomba, ada berapa siswa yang hanya mendaftar lomba pidato?
a. 9 orang
b. 18 orang
c. 20 orang
d. 21 orang
Pembahasan :
S=40 orang
n(P)=27 orang
n(M)=24 orang
n(P U M)'=7 orang
n(P U M)=40 - 7=33
n(P ∩ M)= n(P) + n(M) - n(P U M)
= 27 + 24 - 33
=18 orang
Siswa yang hanya mendaftar lomba pidato=27 - 18=9 orang
25. Dalam suatu test penerimaan calon pegawai, peserta yang diterima adalah yang lulus psikotes maupun kemampuan dasar. Dari 100 orang peserta test ada 60 orang yang lulus uji psikotest, 53 orang lulus uji kemampuan dasar dan 25 orang tidak lulus keduanya. Berapa peserta test yang diterima?
a. 25 orang
b. 38 orang
c. 42 orang
d. 52 orang
Pembahasan :
S=100 orang
n(P)=60 orang
n(K)=53 orang
n(P U K)'=25 orang
Jumlah peserta yang lulus psikotes ataupun kemampuan dasar=
n(P U K)=S - n(P U K)'
=100 - 25=75
Jumlah peserta yang diterima yaitu yang lulus psikotes dan kemampuan dasar
n(P ∩ K)= n(P) + n(K) - n(P U K)
=60 + 53 - 75
=38 orang
SEMOGA BERMANFAAT