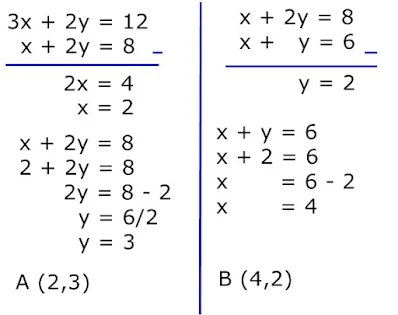SOAL PROGRAM LINEAR KELAS 11 By Bimbel Jakarta Timur
Program linear yaitu metode penentuan nilai optimum persoalan linear. Nilai optimum didapat dari nilai suatu himpunan penyelesaian persoalan linear
Sebuah teknik pemodelan matematika di mana fungsi linier dimaksimalkan atau diminimalkan ketika mengalami berbagai kendala. Teknik ini berguna untuk memandu keputusan kuantitatif dalam perencanaan bisnis, dalam teknik industri, dan—pada tingkat yang lebih rendah—dalam ilmu sosial dan fisika.
Yaitu dengan teknik optimasi untuk sistem kendala linier dan fungsi tujuan linier. Fungsi tujuan mendefinisikan kuantitas yang akan dioptimalkan, dan tujuan dari program linier adalah untuk menemukan nilai dari variabel yang memaksimalkan atau meminimalkan fungsi tujuan.
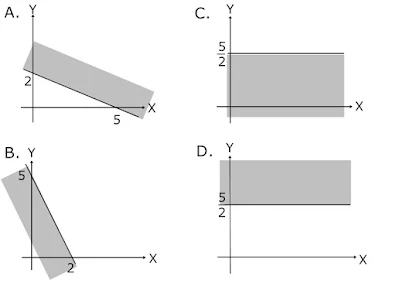
1. Grafik yang menggambarkan pertidaksamaan 2y - 5 ≥ 0 adalah...
Pembahasan :
Soal merupakan pertidaksamaan yang hanya mempunyai variabel y, maka garis yang dimaksud merupakan garis mendatar. Kita selesaikan dulu pertidaksamaannya
2y - 5 ≥ 0
2y ≥ 5
y ≥ 5/2
Perhatikan tanda pertidaksamaan adalah lebih besar (≥), maka daerah penyelesaian ada di atas garis y=5/2
Jawaban : D
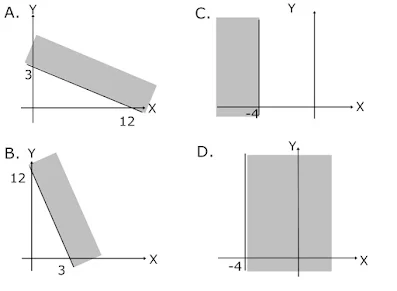
2. Daerah penyelesaian pertidaksamaan 3x + 12 ≤ 0 adalah....
Pembahasan :
Soal merupakan pertidaksamaan yang hanya mempunyai variabel x, maka garis yang dimaksud merupakan garis vertikal. Kita selesaikan dulu pertidaksamaannya
3x + 12 ≤ 0
3x ≤ -12
x ≤ -12/3
x ≤ - 4
Jawaban : C
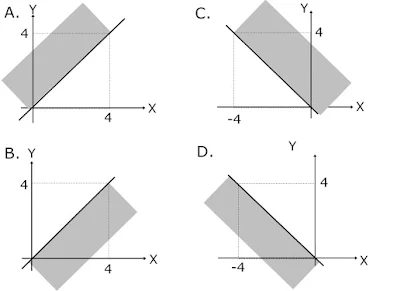
3. Daerah penyelesaian pertidaksamaan x + y ≥ 0 adalah...
Titik yang dilalui garis x + y=0 diantaranya (0,0) dan (-4,4). Tanda pertidaksamaan adalah lebih besar (≥), maka daerah penyelesaian ada di atas atau kanan garis.
Jawaban : C
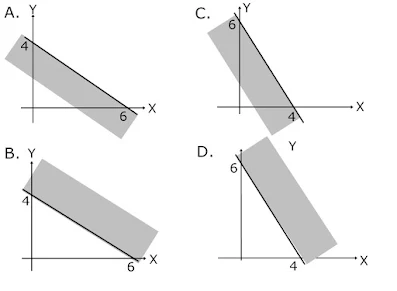
4. Daerah penyelesaian pertidaksamaan 2x + 3y ≤ 12 adalah....
Tentukan titik potong sumbu x dan sumbu y dari garis 2x + 3y=12
⇒ titik potong sumbu x, maka y=0
2x + 3y =12
2x + 3(0)=12
2x =12
x =6
titik potong (6,0)
⇒ titik potong sumbu y, maka x=0
2x + 3y =12
2(0) + 3y=12
3y=12
y=4
titik potong (4,0)
Tanda pertidaksamaan lebih kecil (≤) maka daerah penyelesaian ada di sebelah kiri.
Cara lain yang dapat kita lakukan adalah mengambil salah satu titik uji, apakah merupakan salah satu penyelesaian pertidaksamaan. Contoh, kita ambil titik yang mudah yaitu O (0,0)
2x + 3y ≤ 12
2(0) + 3(0) ≤ 12
0 ≤ 12
karena benar 0 lebih kecil dari 12, maka daerah yang termasuk (0,0) merupakan daerah penyelesaian.
Jawaban : C
5. Daerah penyelesaian pertidaksamaan 4x - 5y ≥ 20 adalah...
⇒ titik potong sumbu x, maka y=0
4x - 5y=20
4x + 0 =20
x=20/4
=5
titik potong (5,0)
⇒ titik potong sumbu y, maka x=0
4x + 5y=20
0 - 5y=20
y=20/-5
=- 4
titik potong (0,-4)
Titik uji (0,0)
4x - 5y ≥ 20
4(0) - 5(0) ≥ 20
0 ≥ 20 merupakan pernyataan yang salah, maka (0,0) bukan salah satu penyelesaian
Jawaban : B
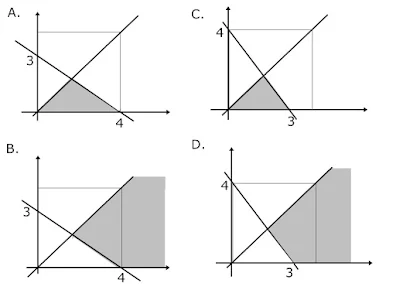
6. Daerah penyelesaian pertidaksamaan 3x + 4y ≤ 12; x - y ≥ 0; x ≥ 0; y ≥ 0 adalah...
Pembahasan :
3x + 4y ≤ 12
⇒ titik potong sumbu x, maka y=0
3x=12
x=4
titik potong (4,0)
⇒ titik potong sumbu y, maka x=0
4y=12
y=3
titik potong (0,3)
tanda pertidaksamaan lebih kecil (≤) maka daerah penyelesaian ada di sebelah kiri.
x - y ≥ 0
di antara dua titik yang dilalui adalah (0,0) dan (4,4)
Tanda pertidaksamaan adalah lebih besar (≥), maka daerah penyelesaian kanan garis.
Jawaban : A
7. Daerah penyelesaian pertidaksamaan 4x + y ≥ 8; x + 2y ≤ 9; x ≥ 0; y ≥ 0 adalah....
3x + 4y ≤ 12
⇒ titik potong sumbu x, maka y=0
3x=12
x=4
titik potong (4,0)
⇒ titik potong sumbu y, maka x=0
4y=12
y=3
titik potong (0,3)
tanda pertidaksamaan lebih kecil (≤) maka daerah penyelesaian ada di sebelah kiri.
x - y ≥ 0
di antara dua titik yang dilalui adalah (0,0) dan (4,4)
Tanda pertidaksamaan adalah lebih besar (≥), maka daerah penyelesaian kanan garis.
y ≥ 0
Tanda pertidaksamaan adalah lebih besar (≥), maka daerah penyelesaian ada di atas garis y=0
x ≥ 0
Tanda pertidaksamaan adalah lebih besar (≥), maka daerah penyelesaian ada di kanan garis x=0
Irisan daerah penyelesaian bisa kamu lihat pada gambar berikut
7. Daerah penyelesaian pertidaksamaan 4x + y ≥ 8; x + 2y ≤ 9; x ≥ 0; y ≥ 0 adalah....
4x + y ≥ 8
⇒ titik potong sumbu x, maka y=0
4x=8
x=2
titik potong (2,0)
⇒ titik potong sumbu y, maka x=0
y=8
titik potong (0,8)
tanda pertidaksamaan lebih besar (≥), maka daerah penyelesaian ada di kanan garis
x + 2y ≤ 9
⇒ titik potong sumbu x, maka y=0
x=9
titik potong (9,0)
⇒ titik potong sumbu y, maka x=0
2y=9
y=9/2
=4,5
titik potong (0,4.5)
tanda pertidaksamaan lebih (≤) maka daerah penyelesaian ada di sebelah kiri.
y ≥ 0
Tanda pertidaksamaan adalah lebih besar (≥), maka daerah penyelesaian ada di atas garis y=0
x ≥ 0
Tanda pertidaksamaan adalah lebih besar (≥), maka daerah penyelesaian ada di kanan garis x=0
Pada gambar di bawah, kita gunakan cara di mana daerah yang diarsir adalah daerah yang bukan merupakan penyelesaian. Irisan daerah penyelesaian akhir adalah daerah yang bersih dari arsiran.
8. Perhatikan gambar berikut !
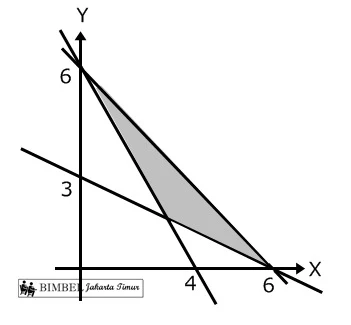
8. Daerah penyelesaian pertidaksamaan x + y ≤ 6, x + 3y ≥ 9; 3x + y ≤ 9; x ≥ 0; y ≥ 0 ditunjukkan ileh daerah nomor...
A.I B. II C. III D. IV
Pembahasan :
x + y y ≤ 6
⇒ titik potong sumbu x, maka y=0
x=6
titik potong (6,0)
⇒ titik potong sumbu y, maka x=0
y=6
titik potong (0,6)
tanda pertidaksamaan lebih (≤) maka daerah penyelesaian ada di sebelah kiri, yang memenuhi adalah I, II, III
x + 3y ≥ 9
⇒ titik potong sumbu x, maka y=0
x=9
titik potong (9,0)
⇒ titik potong sumbu y, maka x=0
3y=9
y=3
titik potong (0,3)
tanda pertidaksamaan lebih besar (≥), maka daerah penyelesaian ada di kanan garis, yang memenuhi adalah I, II dan IV
3x + y ≤ 9
⇒ titik potong sumbu x, maka y=0
3x=9
x=3
titik potong (3,0)
⇒ titik potong sumbu y, maka x=0
y=9
titik potong (0,9)
tanda pertidaksamaan lebih (≤) maka daerah penyelesaian ada di sebelah kiri, yang memenuhi adalah I
Irisan himpunan penyelesaian adalah daerah I
Jawaban : A
9. Sistem pertidaksamaan untuk daerah himpunan penyelesaian pada gambar berikut adalah...
A. x + 2y ≥ 6; 2x + y ≤ 12; x ≥ 0; y ≥ 0
B. x + 2y ≤ 6; 2x + y ≤ 12; x ≥ 0; y ≥ 0
C. x + y ≤ 4; x + 2y ≤ 6; x ≥ 0; y ≥ 0
D. x + y ≥ 4; x + 2y ≤ 6; x ≥ 0; y ≥ 0
Pembahasan :
Garis yang melalui titik (0,3) dan (6,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 3 = x - 0
0 - 3 6 - 0
6(y - 3)=-3(x)
6y - 18=-3x
3x + 6y=18 (disederhanakan dengan dibagi 3)
x + 2y=6
daerah yang diarsir sebelah kiri maka bertanda ≤
x + 2y ≤ 6
Garis yang melalui titik (0,4) dan (4,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 4 = x - 0
0 - 4 4 - 0
4(y - 4)=-4(x)
4y - 16=-4x
4x + 4y=16 (disederhanakan dengan dibagi 4)
x + y=4
daerah yang diarsir sebelah kanan maka bertanda ≥
x + y ≥ 4
Jawaban : D
10. Sistem pertidaksamaan untuk daerah himpunan penyelesaian pada gambar berikut adalah...
A. x + y ≤ 6; x + 2y ≥ 6; 3x + 2y ≤ 12; x ≥ 0; y ≥ 0
B. x + y ≤ 6; x + 2y ≥ 6; 3x + 2y ≥ 12; x ≥ 0; y ≥ 0
C. x + y ≤ 6; x + 2y ≤ 6; 2x + 3y ≤ 12; x ≥ 0; y ≥ 0
D. x + y ≥ 6; x + 2y ≥ 6; 2x + 3y ≥ 12; x ≥ 0; y ≥ 0
Pembahasan :
Garis yang melalui titik (0,3) dan (6,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 3 = x - 0
0 - 3 6 - 0
6(y - 3)=-3(x)
6y - 18=-3x
3x + 6y=18 (disederhanakan dengan dibagi 3)
x + 2y=6
daerah yang diarsir sebelah kanan maka bertanda ≥
x + 2y ≥ 6
Garis yang melalui titik (0,6) dan (6,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 6 = x - 0
0 - 6 6 - 0
6(y - 6)=-6(x)
6y - 36=-6x
6x + 6y=36 (disederhanakan dengan dibagi 6)
x + y=6
daerah yang diarsir sebelah kiri maka bertanda ≤
x + y ≤ 6
Garis yang melalui titik (0,6) dan (4,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 6 = x - 0
0 - 6 4 - 0
4(y - 6)=-6(x)
4y - 24=-6x
6x + 4y=24 (disederhanakan dengan dibagi 2)
3x + 2y=12
daerah yang diarsir sebelah kanan maka bertanda ≥
3x + 2y ≥ 12
Jawaban : B
B. x + 2y ≤ 6; 2x + y ≤ 12; x ≥ 0; y ≥ 0
C. x + y ≤ 4; x + 2y ≤ 6; x ≥ 0; y ≥ 0
D. x + y ≥ 4; x + 2y ≤ 6; x ≥ 0; y ≥ 0
Pembahasan :
Garis yang melalui titik (0,3) dan (6,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 3 = x - 0
0 - 3 6 - 0
6(y - 3)=-3(x)
6y - 18=-3x
3x + 6y=18 (disederhanakan dengan dibagi 3)
x + 2y=6
daerah yang diarsir sebelah kiri maka bertanda ≤
x + 2y ≤ 6
Garis yang melalui titik (0,4) dan (4,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 4 = x - 0
0 - 4 4 - 0
4(y - 4)=-4(x)
4y - 16=-4x
4x + 4y=16 (disederhanakan dengan dibagi 4)
x + y=4
daerah yang diarsir sebelah kanan maka bertanda ≥
x + y ≥ 4
Jawaban : D
10. Sistem pertidaksamaan untuk daerah himpunan penyelesaian pada gambar berikut adalah...
B. x + y ≤ 6; x + 2y ≥ 6; 3x + 2y ≥ 12; x ≥ 0; y ≥ 0
C. x + y ≤ 6; x + 2y ≤ 6; 2x + 3y ≤ 12; x ≥ 0; y ≥ 0
D. x + y ≥ 6; x + 2y ≥ 6; 2x + 3y ≥ 12; x ≥ 0; y ≥ 0
Pembahasan :
Garis yang melalui titik (0,3) dan (6,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 3 = x - 0
0 - 3 6 - 0
6(y - 3)=-3(x)
6y - 18=-3x
3x + 6y=18 (disederhanakan dengan dibagi 3)
x + 2y=6
daerah yang diarsir sebelah kanan maka bertanda ≥
x + 2y ≥ 6
Garis yang melalui titik (0,6) dan (6,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 6 = x - 0
0 - 6 6 - 0
6(y - 6)=-6(x)
6y - 36=-6x
6x + 6y=36 (disederhanakan dengan dibagi 6)
x + y=6
daerah yang diarsir sebelah kiri maka bertanda ≤
x + y ≤ 6
y - y1 = x - x1
y2- y1 x2- x1
y - 6 = x - 0
0 - 6 4 - 0
4(y - 6)=-6(x)
4y - 24=-6x
6x + 4y=24 (disederhanakan dengan dibagi 2)
3x + 2y=12
daerah yang diarsir sebelah kanan maka bertanda ≥
3x + 2y ≥ 12
Jawaban : B
Cara Cepat !
A. x + y ≤ 480; 3x + 10y ≥ 40; x ≥ 0; y ≥ 0
B. x + y ≤ 480; 3x + 10y ≤ 40; x ≥ 0; y ≥ 0
C. x + y ≤ 40; 3x + 10y ≤ 240; x ≥ 0; y ≥ 0
D. x + y ≥ 40; 3x + 10y ≤ 240; x ≥ 0; y ≥ 0
Pembahasan :
mobil=x, bus=y
jumlah mobil dan bus maksimal 40
x + y ≤ 40
luas mobil= 6 m²
luas bus= 20 m²
luas total maksimal 480 m²
6x + 20y ≤ 480 (disederhanakan dengan dibagi 2)
3x + 10y ≤ 240
Jawaban : C
12. Seorang penjahit mendapatkan pesanan dua jenis baju. Untuk memenuhi pesanan tersebut, ia membeli persediaan 30 m kain batik dan 40 m kain polos. Pakaian jenis I yang ia buat membutuhkan 1,5 m kain batik dan 1 m kain polos. Pakaian jenis II membutuhkan 1,2 m kain batik dan 2 m kain polos. Jika pakaian jenis I dinyatakan dengan x dan pakaian jenis II dinyatakan dengan y, model matematika untuk pernyataan tersebut adalah...
A. 5x + 4y ≤ 100; x + 2y ≥ 40; x ≥ 0; y ≥ 0
B. 5x + 4y ≤ 100; x + 2y ≤ 40; x ≥ 0; y ≥ 0
C. 4x + 5y ≤ 100; 2x + y ≤ 40; x ≥ 0; y ≥ 0
D. 4x + 5y ≥ 100; 2x + y ≤ 40; x ≥ 0; y ≥ 0
Pembahasan :
Keterangan pada soal dapat ditulis sebagai berikut :
1,5x + 1,2y ≤ 30 (disederhanakan dengan mengalikan 10/3)
5x + 4y ≤ 100
Kain polos yang dibutuhkan
x + 2y ≤ 40
Jawaban : B
13. Daerah yang diarsir pada gambar berikut merupakan himpunan penyelesaian dari suatu sistem pertidaksamaan. Nilai maksimum 5x + 2y adalah....
Pembahasan :
Garis yang melalui titik (0,5) dan (10,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 5 = x - 0
0 - 5 10 - 0
10(y - 5)=-5(x)
10y - 50=-5x
5x + 10y=50 (disederhanakan dengan dibagi 5)
x + 2y=10
y - y1 = x - x1
y2- y1 x2- x1
y - 8 = x - 0
0 - 8 4 - 0
4(y - 8)=-8(x)
4y - 32=-8x
8x + 4y=32 (disederhanakan dengan dibagi 4)
2x + y=8
Daerah yang diarsir mempunyai sudut pada titik (0,0), (0,5), (4,0) dan perpotongan kedua garis. Tentukan dahulu titik potong kedua garis tersebut
Titik (0,0) ⇒ 5(0) + 2(0)=0
Titik (0,5) ⇒ 5(0) + 2(5)=10
Titik (4,0) ⇒ 5(4) + 2(0)=20
Titik (2,4) ⇒ 5(2) + 2(4)=10 + 8=18
Nilai terbesar adalah 20
Jawaban : C
14. Daerah yang diarsir pada gambar berikut merupakan himpunan penyelesaian dari suatu sistem pertidaksamaan. Nilai minimum 2x + 3y adalah....
Pembahasan :
Garis yang melalui titik (0,4) dan (8,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 4 = x - 0
0 - 4 8 - 0
8(y - 4)=-4(x)
8y - 32=-4x
4x + 8y=32 (disederhanakan dengan dibagi 4)
x + 2y=8
y - y1 = x - x1
y2- y1 x2- x1
y - 9 = x - 0
0 - 9 3 - 0
3(y - 9)=-9(x)
3y - 27=-9x
9x + 3y=27 (disederhanakan dengan dibagi 3)
3x + y=9
Daerah yang diarsir mempunyai sudut pada titik (0,9), (8,0) dan perpotongan dua garis. Kita tentukan titik potong kedua garis tersebut.
Titik (0,9) ⇒ 2(0) + 3(9)=27
Titik (8,0) ⇒ 2(8) + 3(0)=16
Titik (2,3) ⇒ 2(2) + 3(3)=13
Nilai terkecil adalah 13
Jawaban : B
15. Daerah yang diarsir pada gambar berikut merupakan himpunan penyelesaian dari suatu sistem pertidaksamaan. Nilai maksimum 4x - y adalah....
A. 8 B. 16 C. 22 D. 24
Pembahasan :
y - y1 = x - x1
y2- y1 x2- x1
y - 8 = x - 0
0 - 8 4 - 0
4(y - 8)=-8(x)
4y - 32=-8x
8x + 4y=32 (disederhanakan dengan dibagi 4)
2x + y=8
Garis yang melalui titik (0,8) dan (8,0)
y - y1 = x - x1
y2- y1 x2- x1
y - 8 = x - 0
0 - 8 8 - 0
8(y - 8)=-8(x)
8y - 64=-8x
8x + 8y=64 (disederhanakan dengan dibagi 8)
x + y=8
Garis yang melalui titik (4,0) dan tegak lurus garis x + y=8
Gradien garis x + y=8 adalah -1, maka gradien garis yang tegak lurus=1
y - y1 =m(x - x1)
y - 0=1 (x - 4)
y=x - 4
Titik potong garis x + y=8 dan y=x - 4 dapat ditentukan dengan cara substitusi
x + (x - 4)=8
2x - 4=8
2x=8 + 4
2x=12
x=6
y=x - 4=6 - 4=2
titik potong (6,2)
Substitusi setiap titik ke fungsi objektif f(x,y)=4x - y
Titik (0,8) ⇒ 4(0) - 8=- 8
Titik (4,0) ⇒ 4(4) - 0=16
Titik (6,2) ⇒ 4(6) - 2=22
Nilai terbesar adalah 22
Jawaban : C
16. Nilai minimum f(x,y)=5x + 2y - 4 yang memenuhi pertidaksamaan 3x + 2y ≥ 12; x + y ≤ 6; x + 2y ≥ 8 adalah....
A. 4 B. 8 C. 10 D. 12
Pembahasan :
3x + 2y ≥ 12
⇒ titik potong sumbu x, maka y=0x=4
titik potong (4,0)
⇒ titik potong sumbu y, maka x=0
y=6
titik potong (0,6)
daerah penyelesaian di sebelah kanan
x + y ≤ 6
titik potong di (0,6) dan (6,0) daerah penyelesaian di sebelah kiri
x + 2y ≥ 8
titik potong di (0,4) dan (8,0) daerah penyelesaian di sebelah kanan
titik potong garis didapatkan dengan eliminasi
Substitusi setiap titik ke fungsi objektif f(x,y)=5x + 2y - 4
titik potong di (0,4) dan (8,0) daerah penyelesaian di sebelah kanan
titik potong garis didapatkan dengan eliminasi
Titik A(2,3) ⇒ 5(2) + 2(3) - 4=12
Titik B(4,2) ⇒ 5(4) + 2(2) - 4=20
Titik C(0,6) ⇒ 5(0) + 2(6) - 4=8
Nilai terkecil=8
Jawaban : B
Nilai terkecil=8
Jawaban : B
17. Seorang pedagang kue dalam sehari hanya mampu memproduksi 40 buah bolu dan pizza. Modal pembuatan sebuah bolu Rp 30.000,00 dan sebuah pizza modalnya Rp 35.000,00. Ia hanya memiliki modal Rp 1.260.000,00 untuk biaya produksinya. Jika keuntungan yang ia peroleh dari sebuah bolu adalah Rp 11.000,00 dan sebuah pizza keuntungannya Rp 12.500,00 perbuah. Tentukan keuntungan maksimum yang didapat penjual pizza tersebut!
A. Rp 440.000,00
B. Rp 450.000,00
C. Rp 458.000,00
D. Rp 500.000,00
Pembahasan :
Misalkan x=bolu, y=pizza
Jumlah produksi maksimal 40 buah
x + y ≤ 40
Modal sebuah bolu Rp 30.000,00
Modal sebuah pizza Rp 35.000,00
Modal total maksimal Rp 1.260.000,00
30.000x + 35.000y ≤ 1.260.000 (sederhanakan)
6x + 7y ≤ 252
Fungsi keuntungan f(x,y)=11.000x + 12.500y
Titik potong x + y=40 dan 6x + 7y=252 dengan cara substitusi
6(40 -y) + 7y=252
240 - 6y + 7y=252
y=12
x=40 - 12=28
titik potong (28,12)
grafiknya dapat digambarkan sebagai berikut :
Substitusi tiap titik sudut ke fungsi keuntungan f(x,y)=11.000x + 12.500y
(0,36) ⇒ 11.000(0) + 12.500(36)=450.000
(40,0) ⇒ 11.000(40) + 12.500(0)=440.000
(28,12) ⇒ 11.000(28) + 12.500(12)=458.000
Keuntungan terbesar Rp 458.000,00
Jawaban : C
18. Seorang petani akan memberikan pupuk untuk sawahnya. Pupuk yang diberikan setidaknya mengandung 720 gram nitrogen dan 620 gram fosfor. Di koperasi desa terdapat dua macam pupuk yang ditawarkan. Pupuk A harganya Rp 17.500,00 dengan kandungan nitrogen 20 gram dan fosfor 25 gram. Pupuk B harganya Rp 20.000,00 dengan kandungan nitrogen 30 gram nitrogen dan 20 gram fosfor. Petani ingin memberikan pupuk campuran dari kedua jenis pupuk tersebut. Biaya minimum yang harus ia keluarkan untuk membeli pupuk adalah...
A. Rp 510.000,00
B. Rp 530.000,00
C. Rp 620.000,00
D. Rp 630.000,00
Pembahasan :
Pupuk jenis A=x
Pupuk jenis B=y
Jumlah nitrogen minimal
20x + 30y ≥ 720
2x + 3y ≥ 72
Jumlah fosfor minimal
25x + 20y ≥ 620
5x + 4y ≥ 124
Fungsi biaya f(x,y)=17.500x + 20.000y
titik potong 2x + 3y=72 dan 5x + 4y=124 dengan cara eliminasi
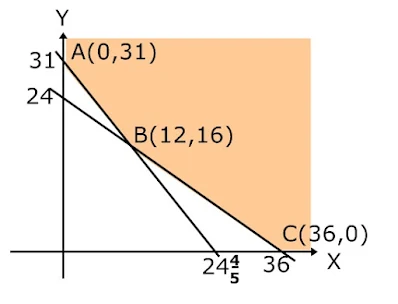
Grafik fungsi pertidaksamaan
A(0,31) ⇒ 17.500(0) + 20.000(31)=620.000
B(12,16) ⇒ 17.500(12) + 20.000(16)=530.000
C(36,0) ⇒ 17.500(36) + 20.000(0)=630.00
Biaya minimal Rp 530.000,00
Jawaban : B
19. Sebuah perusahaan penerbangan menjual tiket kelas ekonomi seharga Rp 600.000,00 dan kelas bisnis Rp 800.000,00. Kelas ekonomi disediakan bagasi sampai berat 25 kg dan kelas bisnis 50 kg. Pesawat hanya mampu mengangkut 200 penumpang dan bagasi seberat 6.250 kg. Berapa banyak penumpang kelas ekonomi dan kelas bisnis yang dapat ditampung agar memperoleh pendapatan maksimum?
A. 150 kelas ekonomi dan 50 kelas bisnis
B. 50 kelas ekonomi dan 150 kelas bisnis
C. 125 kelas ekonomi dan 75 kelas bisnis
D. 75 kelas ekonomi dan 125 kelas bisnis
Pembahasan :
Kelas ekonomi=x
kelas bisnis=y
Jumlah penumpang maksimal 200 orang
x + y ≤ 200
Bagasi kelas ekonomi ≤ 25 kg
Bagasi kelas bisnis ≤ 50 kg
Total bagasi ≤ 6250
25x + 50y ≤ 6.250 (sederhanakan)
x + 2y ≤ 250
Fungsi pendapatan f(x,y)=600.000x + 800.000y
Titik potong x + y=200 dan x + 2y=250 dengan cara substitusi
x + 2y=250
(200 - y) + 2y=250
200 + y=250
y=50
x + y=200
x + 50=200
x=150
titik potong dua garis (150,50)
Garis x + y=200 melalui (0,200) dan (200,0)
Garis x + 2y=250 melalui (0,125) dan (250,0)
Fungsi objektif pendapatan f(x,y)=600.000x + 800.000y
A(0,125) ⇒ 600.000(0) + 800.000(125)=100.000.000
B(150,50) ⇒ 600.000(150) + 800.000(50)=130.000.000
C(200,0) ⇒ 600.000(200) + 20.000(0)=120.000.000
Pendapatan maksimum Rp 130.000.000,00 didapat jika jumlah penumpang ekonomi 150 orang dan penumpang bisnis 50 orang
Jawaban : A
20. Seorang relawan akan menyewa mobil truk dan colt untuk membawa bantuan minimal 450 karung beras dan 320 kardus mie instant. Sebuah truk dapat mengangkut setidaknya 60 karung beras dan 40 kardus mie instant. Mobil colt dapat mengangkut setidaknya 25 karung beras dan 20 kardus mie instant. Jika ongkos sewa truk Rp 250.000,00 dan colt Rp 150.000,00. Berapa jumlah truk dan colt yang harus disewa agar biaya untuk mengantarkan bantuan minimal?
A. 4 truk dan 6 colt
B. 5 truk dan 6 colt
C. 8 truk
D. 18 colt
Pembahasan :
Truk=x
Mobil colt=y
Jumlah beras minimal
60x + 25y ≥ 450 (sederhanakan)
12x + 5y ≥ 90
Jumlah mie instant minimal
40x + 20y ≥ 320 (sederhanakan)
2x + y ≥ 16
Fungsi biaya f(x,y)=250.000x + 150.000y
Garis 12x + 5y=90 melalui (0,18) dan (7½,0)
Garis 2x + y=16 melalui (0,16) dan (8,0)
Titik potong 12x + 5y=90 dan 2x + y=16 dengan cara substitusi
12x + 5y=90
12x + 5(16-2x)=90
12x + 80 - 10x=90
12x - 10x=90 - 80
2x =10
x=5
2x + y=16
2(5) + y=16
10 + y=16
y=6
titik potong (5,6)
Fungsi objektif biaya f(x,y)=250.000x + 150.000y
A(0,18) ⇒ 250.000(0) + 150.000(18)=2.700.000
B(5,6) ⇒ 250.000(5) + 150.000(6)=2.150.000
C(8,0) ⇒ 250.000(8) + 150.000(0)=2.000.000
Biaya minimal Rp 2.000.000,00 jika hanya menyewa truk 8 buah
Jawaban : C
Demikian soal-soal latihan yang dapat kami sajikan. Semoga soal-soal latihan ini dapat membantumu untuk lebih memahami materi program linear.
Jika ada pertanyaan tentang isi artikel silahkan komentar pada artikel yang dimaksud, bukan pada nomer whatsapp yang kami cantumkan. Nomer ini adalah untuk keperluan pendaftaran dan informasi bimbel, bukan jasa tanya jawab soal.
0 Komentar: