Dimensi tiga yaitu bangun dengan ukuran yang terdiri atas panjang, lebar dan tinggi. Dimensi tiga juga sering disebut juga dengan bangun ruang.
1. Kubus ABCD.EFGH dengan panjang rusuk 6 cm. Diketahui titik P berada di tengah-tengah FG. Jarak titik P ke titik A adalah....
A. 6√2 cm
B. 6√3 cm
C. 6√6 cm
D. 9 cm
E. 9√2 cm
Pembahasan :
Perhatikan gambar berikut !
Untuk menghitung jarak titik P ke titik A, kita tinjau segitiga AFP yang siku-siku di F. AF adalah diagonal sisi sehingga panjangnya 6√2 cm dan FP=3 cm.
Hitung AP dengan phytagoras
AP²=AF² + FP²
AP²=(6√2)² + 3²
=72 + 9
=81
AP=√81=9 cm
Jawaban D
2. Kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak titik E ke garis BG adalah....
A. 4√2 cm
B. 4√3 cm
C. 4√6 cm
D. 8 cm
E. 8√2 cm
Pembahasan :
Perhatikan gambar berikut !
Kita tinjau segitiga EBG. Karena EB, BG dan EG adalah diagonal bidang, maka segitiga EBG adalah segitiga sama sisi dengan panjang sisi 8√2 cm dan sudut 60°.
Jarak E ke garis BG adalah garis yang ditarik dari titik E yang tegak lurus dengan garis BG yaitu EE'.
Perhatikan segitiga EBE' !
sin 60°=EE'
EB
½√3 = EE'
8√2
EE'= ½√3 . 8√2
=4√6 cm
Jawaban : C
3. Kubus ABCD.EFGH dengan panjang rusuk 8 cm. Titik M adalah perpanjangan rusuk FG sehingga GM=4 cm dan FM=12 cm. Jarak titik M ke EB adalah...
A. 4√2 cm
B. 4√3 cm
C. 4√6 cm
D. 4√11 cm
E. 4√13 cm
Pembahasan :
Perhatikan gambar berikut !
Jarak titik M ke EB adalah panjang garis yang ditarik dari titik M dan tegak lurus EB. Kita tinjau segitiga MEB dengan EM dan BM sama panjang. Tinjau segitiga EMF dahulu untuk menghitung panjang EM.
EM²=AF² + FM²
EM²=8² + 12²
=64 + 144
=208
EM=√208=4√13 cm
Sekarang kita lihat segitiga EMB dimana EB adalah diagonal bidang sehingga panjangnya 8√2 cm. Panjang EM'=½EB=4√2 cm.
Maka panjang MM' dapat dicari dengan Phytagoras
MM'²=EM² - EM'²
=(4√13)²-(4√2)²
=208 - 32
=176
MM'= √176=4√11 cm
Jawaban : D
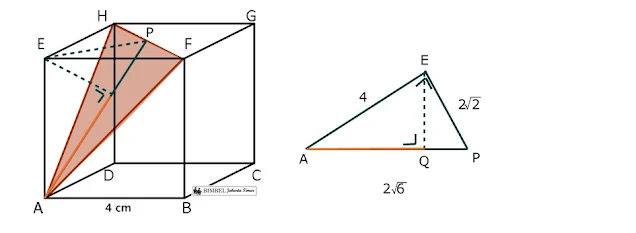
4. Perhatikangambar kubus ABCD.EFGH berikut !
Panjang proyeksi EA pada bidang AHF adalah.....
A. 4 cm
B. 4√3 cm
C. 4/3√3 cm
D. 4/3√6 cm
E. 6 cm
Pembahasan :
Perhatikan gambar berikut !
Garis AP mewakili bidang AFH, maka kita tinjau segitiga AEP. Panjang EP adalah 2√2 karena besarnya 1/2 dari diagonal bidang.
AP²=AE² + eP²
AP²=4² + (2√2)²
=16 + 8
=24
AP=√24=2√6 cm
Panjang proyeksi EA pada bidang AHF adalah ruas AQ dimana Q adalah titik potong garis yang ditarik dari titik E dan tegak lurus AP.
cos A (tinjau ΔAEQ)=cos A (tinjau ΔAEP)
AQ / AE =AE / AP
AQ / 4 =4 / 2√6
AQ =4 . 4 / 2√6
=8 / √6
= D. 4/3√6 cm
Jawaban : D
A. 2 √6 cm
B. 4 cm
C. 4√2 cm
D. 4√3 cm
E. 4√6 cm
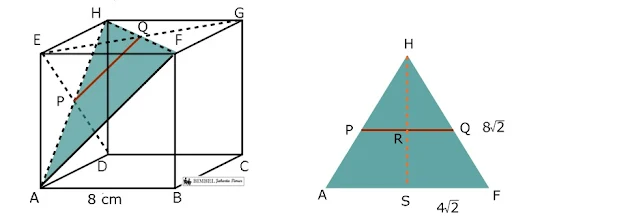
Pembahasan :
Perhatikan gambar berikut !
PQ dan AF berada pada bidang AFH yang merupakan segitiga sama sisi dengan panjang sisi 8√2 cm. Jarak PQ ke AF diwakili ras RS yang panjangnya 1/2 dari HS.
HS²=HF² - SF²
=(8√2)² - (4√2)²
=128 - 32
=96
HS= √96= 4√6 cm
Maka RS=2√6 cm
Jawaban : A
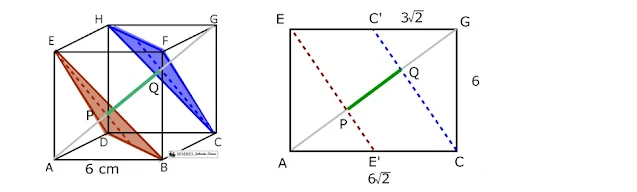
6. Diketahuikubus ABCD.EFGH dengan rusuk 6 cm. Jarak Bidang EBD dan HFC adalah ...
A. 2√3 cm
B. 2√6 cm
C. 4√2 cm
D. 4√3 cm
E. 6 cm Pembahasan :
Perhatikan gambar berikut !
Jarak Bidang EBD dan HFC adalah jarak PQ. Perhatikan bidang ACGE dimana AC dan EG adalah diagonal bidang kubus dan AG adalah diagonal ruang kubus. Maka AC= 6√2 cm dan AG= 6√3 cm
PQ=1/3 AG
=1/3 x 6√3
=2√3 cm
Jawaban : A
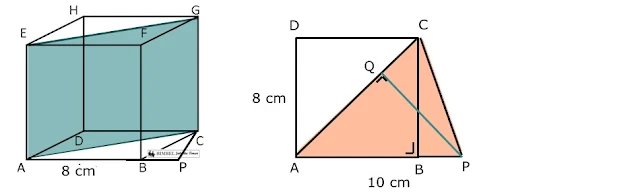
7. Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Titik P terletak pada perpanjangan AB sehingga BP : AB=1 : 4. Jarak titik P ke bidang ACGE adalah...
A. 4√2 cm
B. 4√3 cm
C. 4√6 cmD. 5√2 cm
E. 5√3 cm
Pembahasan :
Perhatikan gambar berikut !
Jarak titik P ke bidang ACGE adalah PQ. Panjang PQ dapat ditentukan dengan rumus luas segitiga APC.
Alas1 =AP=10 cm
Tinggi1 =BC=8 cm
Alas2 =AC=8√2 cm
Tinggi2 =PQ=?
Luas APC1 = Luas APC2
Alas1 x Tinggi1= Alas2 x Tinggi2
10 x 8 = 8√2 x PQ
PQ=10 x √2
√2 √2
=5√2 cm
Jawaban : D
8. Diketahui kubus ABCD.EFGH dengan rusuk 6 cm. Titik P merupakan perpotongan diagonal EG dan HF. Proyeksi garis AP pada bidang alas adalah...
A. 3√2 cm
B. 3√3 cm
C. 3√6 cm
D. 6 cm
E. 6√2 cm
Pembahasan :
Perhatikan gambar berikut !
Proyeksi titik P pada bidang alas adalah P', maka proyeksi garis AP pada bidang alas adalah AP'.
AP'=½ diagonal bidang AC
=½ x 6√2
=3√2 cm
Jawaban A
9. Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Titik P terletak di tengah AD dan titik Q terletak di tengah EF. Cosinus sudut yang dibentuk oleh PQ dan bidang alas adalah....
A. 1/3
B. 1/3√2
C. 1/3√3
D. 1/3√6
E. 2/3
Pembahasan :
Perhatikan gambar berikut !
Sudut yang dibentuk oleh PQ dan bidang alas ditunjukkan oleh sudut QPQ'.
PQ²=PQ'² + Q'Q²
=(4√2)² + 8²
=32 + 64
=96
PQ= √96=4√6 cm
Cosinus QPQ'=samping
miring
=4√2
4√6
= 1 . √3
√3 √3
=1/3 √3
Jawaban : C
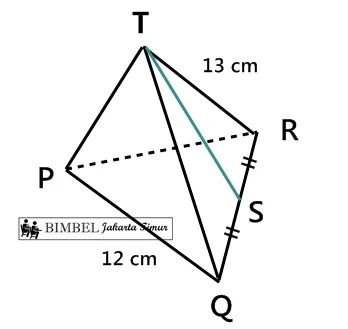
10. Bangun T.PQR di bawah ini adalah limas dengan panjang rusuk alas 12 cm dan rusuk tegak 13 cm.
Jarak titik T ke PS adalah....
A. 4√3 B. 6√3 C. 11 D. √133 E. 12
Pembahasan :
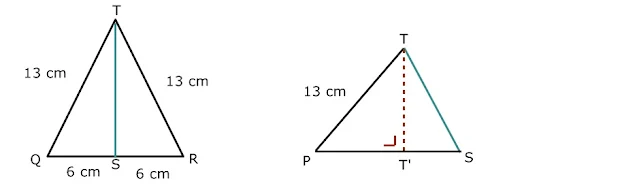
Perhatikan gambar berikut !
Panjang TS adalah
TS²=TR² - SR²
=13² - 6²
=169 - 36
=133
TS=√133 cm
Panjang TS adalah
PS²=PR² - SR²
=12² - 6²
=144 - 36
=108
PS=√108=6√3 cm
Terlebih dahulu kita tentukan panjang PT' dengan rumus cosinus sudut P pada segitiga PTS
cos P=PT² + PS² - TS²
2.PT.PS
PT' =13² + 6√3² - √133²
PT 2.13.6√3
PT' = 169 + 108 - 133
13 2.13.6√3
PT' = 144 . √3
12√3 √3
=4√3 cm
Jarak titik T ke PS adalah TT', kita tentukan dengan phytagoras
TT'²=PT² - PT'²
=13² - 4√3²
=169 - 48
=121
TT'=√121=11 cm
Jawaban : C
11. Limas T.ABCD dengan panjang rusuk AB=8 cm dan BC=6 cm. Jika tinggi limas adalah 12 cm, jarak titik A ke rusuk TC adalah....
A. 9 cm
B. 9,23 cm
C. 9,36 cm
D. 9,78 cm
E. 10 cm
Pembahasan :
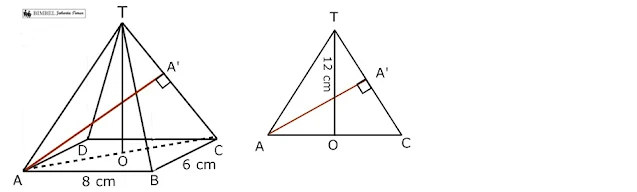
Perhatikan gambar berikut !
Panjang diagonal alas AC adalah
AC²=AB² + BC²
=8² + 6²
=64 + 36
=100
AC= √100=10 cm
Panjang rusuk tegak TA=TC
TC²=TO² + OC²
=12² + 5²
=144 + 25
=169
AC= √169=13 cm
Jarak titik A ke rusuk TC dapat dicari dengan meninjau segitiga TAC
Alas1=AC=10 cm
Tinggi1=TO=12 cm
Alas2=TC=13 cm
Tinggi2=AA'=?
Alas1 x Tinggi1 = Alas2 x Tinggi2
10 x 12 =13 x AA'
AA'= 120 =9,23 cm
13
Jawaban : B
12. Limas T.ABCD dengan alas berbentuk persegi dan panjang AB=12 cm dan panjang rusuk tegak 12√2 cm. Jika titik P berada di tengah TB, maka jarak titik P ke bidang alas adalah....
A. 2√10 cm
B. 3√6 cm
C. 3√10 cm
D. 4√6 cm
E. 3√10 cm
Pembahasan :
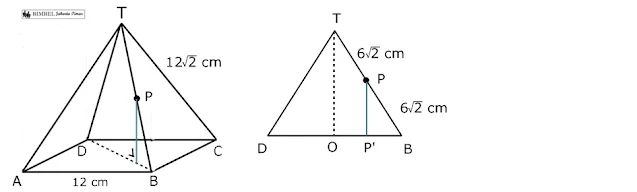
Perhatikan gambar berikut !
Panjang diagonal alas BD adalah
BD²=CD² + BC²
=12² + 12²
=144 + 144
=288
BD= √288=12√2 cm
P'B=½ OB=¼ BD
=¼ x 12√2 cm
=3√2 cm
Jarak titik P ke bidang alas adalah PP'
PP'²=PB² - P'B²
=6√2² - 3√2²
=72 - 18
=54
PP'= √54=3√6 cm
Jawaban : B
Pembahasan :
Perhatikan gambar berikut !
Panjang TS adalah
TS²=TR² - SR²
=13² - 6²
=169 - 36
=133
TS=√133 cm
Panjang TS adalah
PS²=PR² - SR²
=12² - 6²
=144 - 36
=108
PS=√108=6√3 cm
Terlebih dahulu kita tentukan panjang PT' dengan rumus cosinus sudut P pada segitiga PTS
cos P=PT² + PS² - TS²
2.PT.PS
PT' =13² + 6√3² - √133²
PT 2.13.6√3
PT' = 169 + 108 - 133
13 2.13.6√3
PT' = 144 . √3
12√3 √3
=4√3 cm
Jarak titik T ke PS adalah TT', kita tentukan dengan phytagoras
TT'²=PT² - PT'²
=13² - 4√3²
=169 - 48
=121
TT'=√121=11 cm
Jawaban : C
11. Limas T.ABCD dengan panjang rusuk AB=8 cm dan BC=6 cm. Jika tinggi limas adalah 12 cm, jarak titik A ke rusuk TC adalah....
A. 9 cm
B. 9,23 cm
C. 9,36 cm
D. 9,78 cm
E. 10 cm
Pembahasan :
Perhatikan gambar berikut !
Panjang diagonal alas AC adalah
AC²=AB² + BC²
=8² + 6²
=64 + 36
=100
AC= √100=10 cm
Panjang rusuk tegak TA=TC
TC²=TO² + OC²
=12² + 5²
=144 + 25
=169
AC= √169=13 cm
Jarak titik A ke rusuk TC dapat dicari dengan meninjau segitiga TAC
Alas1=AC=10 cm
Tinggi1=TO=12 cm
Alas2=TC=13 cm
Tinggi2=AA'=?
Alas1 x Tinggi1 = Alas2 x Tinggi2
10 x 12 =13 x AA'
AA'= 120 =9,23 cm
13
Jawaban : B
12. Limas T.ABCD dengan alas berbentuk persegi dan panjang AB=12 cm dan panjang rusuk tegak 12√2 cm. Jika titik P berada di tengah TB, maka jarak titik P ke bidang alas adalah....
A. 2√10 cm
B. 3√6 cm
C. 3√10 cm
D. 4√6 cm
E. 3√10 cm
Pembahasan :
Perhatikan gambar berikut !
Panjang diagonal alas BD adalah
BD²=CD² + BC²
=12² + 12²
=144 + 144
=288
BD= √288=12√2 cm
P'B=½ OB=¼ BD
=¼ x 12√2 cm
=3√2 cm
Jarak titik P ke bidang alas adalah PP'
PP'²=PB² - P'B²
=6√2² - 3√2²
=72 - 18
=54
PP'= √54=3√6 cm
Jawaban : B
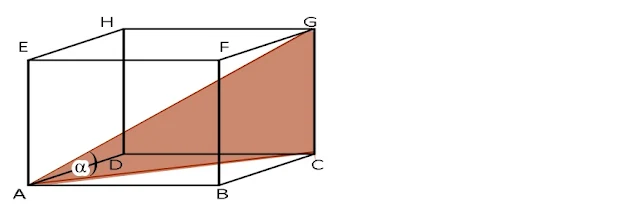
13. Balok ABCG.EFGH dengan panjang AB=BC=6 cm dan AE=4 cm. Sudut 𝝰 adalah sudut antara garis AG dengan bidang alas. Nilai cos 𝝰 adalah....
A. 3 √2
10
B. 3 √5
5
C. 3 √10
5
D. 3 √10
10
E. 3 √2
5
Pembahasan :
Perhatikan gambar berikut !
AC²=AB² + BC²
=6² + 6²
=36 + 36
=72
AC= √72=6√2 cm
AG²=AC² + GC²
=6√2² + 4²
=72 + 16
=80
AG= √80=4√5 cm
cos 𝝰= AC
AG
= 6√2 . √5
4√5 √5
=6√10
20
= 3 √10
10
Jawaban : D
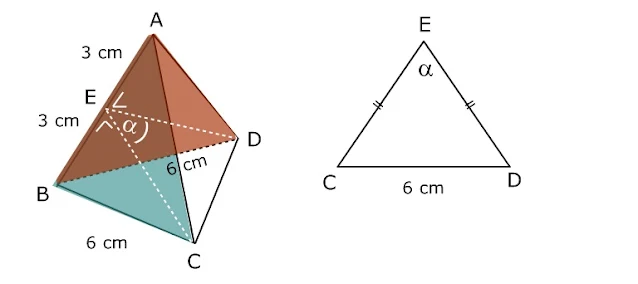
14. Sebuah bidang 4 beraturan A.BCD dengan panjang rusuk 6 cm. Nilai cosinus sudut antara bidangABC dan bidang ABD adalah ...
A. 1/3 B. 1/2 C. 1/3√3 D. 2/3 E. 1/2√3
EC²=BC² - BE²
=6² - 3²
=36 - 9
=27
EC=√27=3√3 cm
cos 𝝰=EC² + ED² - CD²
2.EC.ED
= 3√3² + 3√3² - 6²
2.3√3.3√3
= 27 + 27 - 36
2.27
= 18
54
=1/3
Jawaban : A
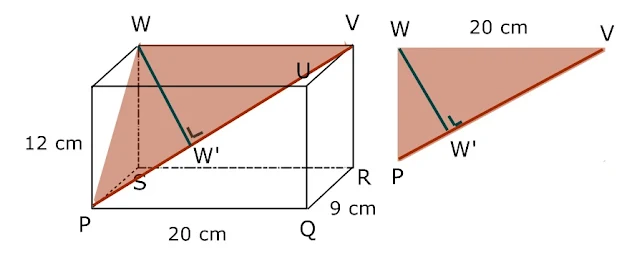
15. Diketahui balok PQRS.TUVW dengan panjang PQ=20 cm, QR=9 cm dan PT=12 cm. Jarak titik W ke diagonal ruang PV adalah....
A. 9 cm
B. 12 cm
C. 15 cm
D. 20 cm
E. 25 cm
Pembahasan :
Perhatikan gambar berikut !
PW²=PT² + TW²
=12² + 9²
=144 + 81
=225
PW= √225=15 cm
PV²=PW² + WV²
=15² + 20²
=225 + 400
=625
PW= √625=25 cm
Jarak titik W ke diagonal ruang PV=WW'
WW'= PW . WV
PV
= 15 . 20
25
=12 cm
Jawaban : B
16. Pada kubusABCD. EFGH sudut θ adalah sudut antara bidang BDE dengan bidang BGD. Nilaidari sin θ adalah ...
=6² - 3²
=36 - 9
=27
EC=√27=3√3 cm
cos 𝝰=EC² + ED² - CD²
2.EC.ED
= 3√3² + 3√3² - 6²
2.3√3.3√3
= 27 + 27 - 36
2.27
= 18
54
=1/3
Jawaban : A
15. Diketahui balok PQRS.TUVW dengan panjang PQ=20 cm, QR=9 cm dan PT=12 cm. Jarak titik W ke diagonal ruang PV adalah....
A. 9 cm
B. 12 cm
C. 15 cm
D. 20 cm
E. 25 cm
Pembahasan :
Perhatikan gambar berikut !
PW²=PT² + TW²
=12² + 9²
=144 + 81
=225
PW= √225=15 cm
PV²=PW² + WV²
=15² + 20²
=225 + 400
=625
PW= √625=25 cm
Jarak titik W ke diagonal ruang PV=WW'
WW'= PW . WV
PV
= 15 . 20
25
=12 cm
Jawaban : B
16. Pada kubusABCD. EFGH sudut θ adalah sudut antara bidang BDE dengan bidang BGD. Nilaidari sin θ adalah ...
A. 1/4√3
B. 1/2√3
C. 2/3√3
D. 1/2√2
E. 2/3√6
B. 1/2√3
C. 2/3√3
D. 1/2√2
E. 2/3√6
Pembahasan :
Perhatikan gambar berikut !
EO=OG
EO²=EA² + AO²
=8² + 4√2²
=64 + 32
=96
EO= √96=4√6 cm
cos θ = EO² + OG² - EG²
2.EO.OG
= 4√6² + 4√6² - 8√2²
2.4√6.4√6
= 96 + 96 - 128
2.96
= 64
192
= 1
3
sin²θ + cos²θ=1
sin²θ + (1/3)²=1
sin²θ=1 - 1/9=8/9
sinθ =2√2
3
Jawaban : C
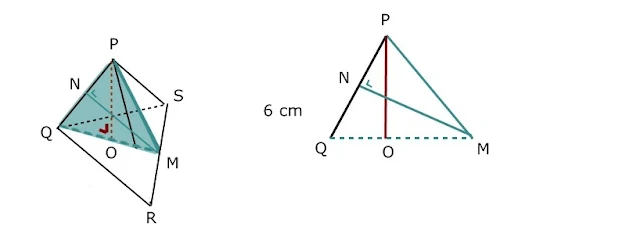
17. Bidang empat beraturan P.QRS mempunyai rusuk 6 cm. Tinggi bidang empat tersebut adalah....
A. 2√2 cm
B. 2√3 cm
C. 2√6 cm
D. 3√2cm
E. 3√3 cm
Pembahasan :
Perhatikan gambar berikut !
Titik M berada di tengah RS sehingga PM ⊥ RS dan QM ⊥RS.
Panjang rusuk PM=QM
PM²=PS² - MS²
=6² - 3²
=36 - 9
=27
PM= √27=3√3 cm, QM=PM
MN²=PM² - PN²
= 3√3² - 3²
=27 - 9
=18
MN= √18=3√2 cm
Tinggi limas adalah PO dapat dicari dengan meninjau segitiga PQM
Alas1 =QM= 3√3 cm
Tinggi1 =PO=?
Alas2 =PQ=6 cm
Tinggi2 =MN= 3√2 cm
Alas1 x Tinggi1 = Alas2 x Tinggi2
3√3 x PO =6 x 3√2
PO = 18√2 =2√6 cm
3√3
Jawaban : C
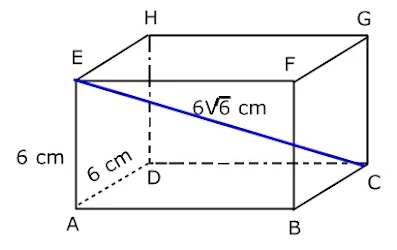
18. Diketahui balok ABCD.EFGH dengan panjang AE=AD=12 cm dan EC=6√6 cm. Volume balok tersebut adalah....
A. 216 cm³
B. 216√6 cm³
C. 324 cm³
D. 324√2 cm³
E. 432 cm³
Pembahasan :
Perhatikan gambar balok berikut!
EC merupakan diagonal ruang balok, sedangkan AD=lebar dan AE=tinggi.
Kita tentukan panjang balok dengan rumus panjang diagonal ruang
Dr² =p² + l² + t²
6√6²=p² + 6² + 6²
216 =p² + 36 + 36
p² =216 - 72
=144
p =√144=12 cm
Volume balok=p x l x t
=12 x 6 x 6
= 432 cm³
Jawaban : E
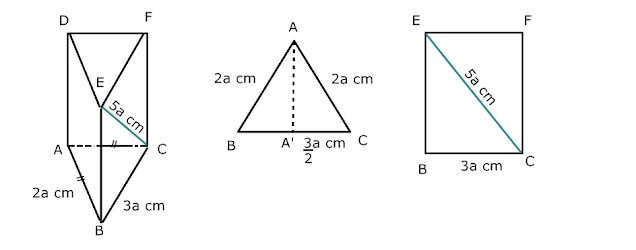
19. Diketahui prisma segitiga ABC.DEF dengan panjang AB=AC=2a cm, BC=3a cm dan CE=5a cm. Volume prisma tersebut adalah....
A. 6√7a³ cm³
B. 6√6a³ cm³
C. 6√2a³ cm³
D. 4√7a³ cm³
E. 4√3a³ cm³
Pembahasan :
Perhatikan gambar berikut !
Untuk menghitung volume prisma, terlebih dahulu tentukan luas alas prisma.
Tentukan terlebih dahulu tinggi segitiga yaitu AA'
AA'²=AC² - A'C²
=(2a)² - (3/2 a)²
=4a² - 9/4 a²
=7a²
AA'=√7 a cm
L= ½ x alas x tinggi
= ½ x 3a x √7 a
=3/2 √7 a² cm²
Tinggi prisma adalah BE
BE²=EC² - BC²
=(5a)² - (3a)²
=25a² - 9a²
=16a²
BE=4a
Volume prisma=Luas alas x tinggi prisma
= 3/2 √7 a² x 4a
=6√7a³ cm³
Jawaban : A
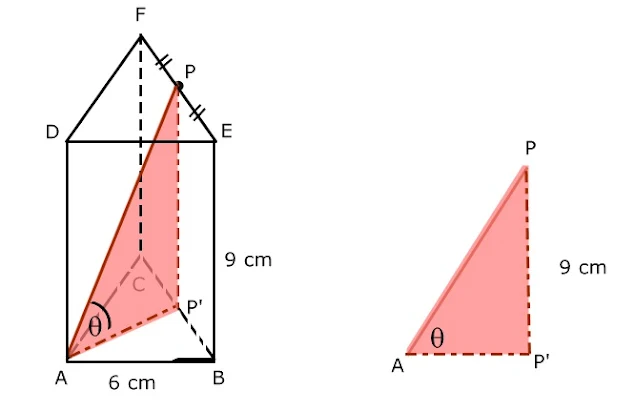
20. Diketahui prisma segitiga ABC.DEF dengan panjang rusuk alas 6 cm serta rusuk tegak 9 cm. Titik P terletak di tengah rusuk EF. Jika θ adalah sudut yang dibentuk AP dengan bidang alas, maka besar sudut θ adalah....
A. 30°
B. 45°
C. 60°
D. 90°
E. 120°
Pembahasan :
Perhatikan gambar berikut !
AP'²=AB² - P'B²
=6² - 3²
=36 - 9
=27
AP'= √27=3√3 cm
tan θ= PP'
AP'
= 9
3√3
= √3
arc tan √3=60°
Besar sudut θ =60°
Jawaban : C
Demikian soal-soal latihan yang dapat kami sajikan. Semoga soal-soal latihan ini dapat membantumu untuk lebih memahami materi dimensi tiga.
Jika ada pertanyaan tentang isi artikel yang dibuat website ini silahkan komentar pada artikel yang dimaksud, bukan pada nomer whatsapp yang kami cantumkan. Nomer ini adalah untuk keperluan pendaftaran dan informasi bimbel, bukan jasa tanya jawab soal.