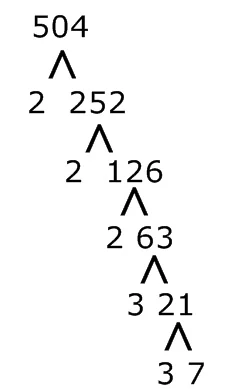Bilangan bulat himpunan bilangan-bilangan terdiri bilangan-bilangan : cacah, asli, prima, komposit, nol, satu, negatif, ganjil dan genap.
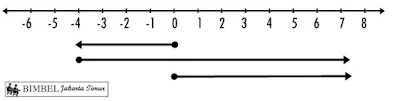
1. Kalimat matematika yang benar untuk gambar berikut adalah….
A. 0 -4 + 7=3B. -4 + 7=11
C. -4 + 11=7
D. 11 - 4=7
Pembahasan :
Garis panah pertama 4 satuan ke kiri=-4
Garis panah kedua 11 satuan ke kanan=11
Garis panah ketiga (hasil) 7 satuan ke kanan=7
-4 + 11=7
Jawaban : C
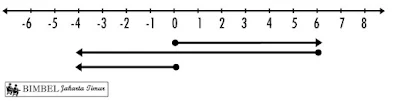
2. Kalimat matematika yang benar untuk gambar berikut adalah….
A. 6 + 4=10
B. 6 - 4=2
C. 6 -4=10
D. 6 - 10=-4
Pembahasan :
Garis panah pertama 6 satuan ke kanan=6
Garis panah kedua 10 satuan ke kiri=- 10
Garis panah ketiga (hasil) 4 satuan ke kiri= - 4
6 - 10=- 4
Jawaban : D
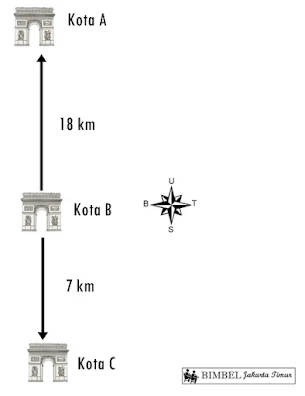
3. Kota A terletak 18 km di sebelah Utara kota B, sedangkan kota C berada 7 km di sebelah Selatan kota B. Jarak kota A dan kota C adalah....
A. 5 km
B. 11 km
C. 25 km
D. 32 km
Pembahasan :
Perhatikan gambar berikut!
Jarak kota A ke kota B=18 km dan jarak kota B ke kota C 7 km, maka jarak kota A dan kota C adalah 18 + 7=25 km
Jawaban : C
4. Kalimat matematika berikut yang merupakan sifat asosiatif adalah....
A. - 35 + (76 + 24)= (-35 + 76) + 24
B. (-35 + 76) + 24=35 - (76 + 24)
C. 89 x 21=21 x 89
D. 17 x (34 + 16)=(17 x 34) + (17 x 16)
Pembahasan :
Asosiatif adalah sifat pengelompokan dari tiga bilangan di mana dua bilangan dikelompokkan untuk dihitung terlebih dahulu. Dua bilangan yang dikelompokkan atau dihitung terlebih dahulu bisa dua bilangan pertama ataupun dua bilangan terakhir. Hasil perhitungannya akan sama besar.
Contoh sifat asosiatif :
- 35 + (76 + 24)= (-35 + 76) + 24
- 35 + 100 =41 + 24
65 = 65
Jawaban : A
5. Urutan bilangan bulat dari yang terkecil hingga terbesar yang benar adalah....
A. 1, 3, -5
B. -3, 0, 2
C. 5, -3, 0
D. 2, 3, -6
Pembahasan :
Perhatikan garis bilangan
bilangan di sebelah kiri nilainya lebih kecil dari bilangan di sebelah kanan
-3 lebih kecil dari 0, dan 0 lebih kecil dari 2
Jawaban : B
6. 72 + 16 + n=54
Nilai n yang benar untuk kalimat matematika di atas adalah....
A. 2
B. 24
C. 34
D. 42
Pembahasan :
72 + 16 + n=54
88 + n=54
nilai n mengurangi bilangan 88 menjadi 54,maka
n=88 - 54
=34
Jawaban : C
7. 87 + (-13) - p = 90
Nilai n yang benar untuk kalimat matematika di atas adalah....
A. -16
B. -3
C. 3
D. 16
Pembahasan :
87 + (-13) - p=90
74 - p=90
p=74 - 90
p=- 16
Jawaban : A
A. - 79
B. - 65
C. 65
D. 79
Pembahasan :
4 x (-18) + (-42) : 6
=-72 + (-7)
=-79
Jawaban : A
Pembahasan :
4 x (-18) + (-42) : 6
=-72 + (-7)
=-79
Jawaban : A
9. 239 + 28 - (-71) + (-234)=...
Hasil dari operasi perhitungan di atas adalah....
A. -164
B. -104
C. 64
D. 104
Pembahasan :
239 + 28 - (-71) + (-234)
=239 + 28 + 71 - 234
=104
Jawaban : D
10. -43 - 57 + 208 + (-29)=.....
Hasil dari operasi perhitungan di atas adalah....
A. -79
B. -49
C. 79
D. 109
Pembahasan :
-43 - 57 + 208 + (-29)
=- 100 + 208 - 29
=108 - 29
=79
Jawaban : C
11. Hasil dari 1.285 - 125 : (-5) + (-26) x 15=....
A. 870
B. 920
C. 1650
D. 1700
Pembahasan :
1.285 - 125 : (-5) + (-26) x 15
=1.285 - (-25) + (-390)
=1.285 + 25 - 390
=920
Jawaban : B
12. Hasil dari 56 : (7 - 15) + 23 x (15 - 7)=
A. 177
B. 184
C. 191
D. 192
Pembahasan :
56 : (7 - 15) + 23 x (15 - 7)
=56 : (-8) + 23 x 8
=-7 + 184
=177
Jawaban : A
13. Pengerjaan (85 + 16) x 8=(85 x 8)+ (16 x 8) menggunakan sifat ....
A. identitas
B. asosiatif
B. asosiatif
C. distributif
D.komutatif
Pembahasan :
Soal di atas menunjukkan jumlah dua bilangan di dalam kurung masing- masing disebar menjadi perkalian dengan bilangan 8. Sifat tersebut adalah penyebaran atau distributif.
Jawaban : C
Pembahasan :
Soal di atas menunjukkan jumlah dua bilangan di dalam kurung masing- masing disebar menjadi perkalian dengan bilangan 8. Sifat tersebut adalah penyebaran atau distributif.
Jawaban : C
A. -102 + 79=79 + (-102)
B. (23 + 19) + (-44)=23 + (19 + (-44))
C. (18 + 74) x 15=18 + (74 x 15)
D. (18 + 74) x 15=(18 x 15) + (74 x 15)
Pembahasan :
Komutatif adalah sifat pertukaran. Dua bilangan atau lebih yang mempunyai operasi hitung jumlah atau kali, ditukar posisinya untuk dihitung. Hasil sebelum dan sesudah ditukar akan sama.
Jawaban : A
15. Suhu di kota London pada pukul 07.00 pagi adalah -7℃. Menjelang siang, suhu di kota itu naik 2℃ setiap setengah jam. Berapa suhu di kota London pada pukul 11.00 ?
A. 1℃
B. 9℃
C. 11℃
D. 17℃
Pembahasan :
Suhu awal= -7℃
Setiap setengah jam naik 2℃
Dari pukul 07.00 ke pukul 11.00 adalah 4 jam.
Suhu naik sebanyak 4 : ½=8 kali.
Suhu pada pukul 11.00
=-7 + 2 x 8
=-7 + 16
= 9℃
Jawaban : B
A. 17
B. 18
C. 19
D. 20
Pembahasan :
10 tim saling bertanding melawan tim lain, maka setiap tim melakukan 9 kali pertandingan.
Hasil tanding tim Pelita=5 menang, 3 kalah, 1 seri
Nilai
=(5 x 4) + (3 x -1) + (1 x 1)
=20 - 3 + 1
=18
Jawaban : B
A. 8 km sebelah Utara kota C
B. 8 km sebelah Selatan kota C
C. 32 km sebelah Utara kota C
D. 32 km sebelah Selatan kota C
Pembahasan :
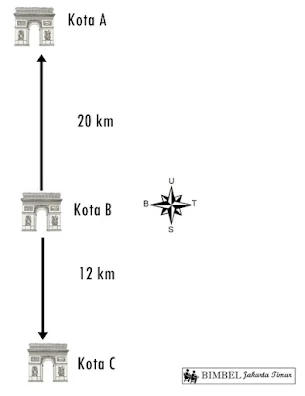
Perhatikan gambar!
Dilihat dari kota C, maka letak kota A adalah 20 - (-12)=32 km sebelah Utara
Jawaban : C
18. Pada sebuah ujian diberikan 30 soal. Setiap jawaban benar mendapat nilai 3, jawaban salah diberi nilai -2 dan jika tidak dijawab nilainya 1. Emma dapat mengerjakan 26 soal tetapi hanya 24 yang benar. Berapa nilai yang didapatkan Emma?
A. 68
B. 70
C. 72
D. 78
Pembahasan :
Jumlah soal=30
Jumlah jawaban benar=24
Jumlah jawaban salah=26 - 24=2
Jumlah tidak dijawab=30 - 26=4
Nilai benar=3
Nilai salah=-2
Nilai tidak dijawab=1
Jumlah nilai
=(24 x 3) + (2 x -2) + (4 x 1)
=72 - 4 + 4
=72
Jawaban : C
Baca juga : Soal Cerita Bilangan Bulat
19. Faktorisasi prima dari 504 adalah....
A. 2³ x 3³
B. 2² x 3² x 7
C. 2³ x 3² x 7
D. 2² x 3 x 8
Pembahasan :
Pohon faktor dari 504 adalah
Maka faktorisasi prima dari 504 adalah 2³ x 3² x 7
Jawaban : C
20. FPB dari 132, 108 dan 84 adalah....
A. 12
B. 15
C. 16
D. 18
Pembahasan :
Faktorisasi prima
132= 2² x 3 x 11
108= 2² x 3³
84= 2² x 3 x 7
FPB adalah faktor prima yang sama yaitu 2 dan 3 serta pangkat yang terkecil
FPB= 2² x 3=12
Jawaban : A
21. KPK dari 24, 30 dan 45 adalah....
A. 96
B. 320
C. 360
D. 480
Pembahasan :
Faktorisasi prima
24=2³ x 3
30=2 x 3 x 5
45=3² x 5
KPK adalah semua faktor prima yang ada serta pangkat yang terbesar
KPK= 2³ x 3² x 5=360
Jawaban : C
A. 8 kalung
B. 12 kalung
C. 18 kalung
D. 24 kalung
Pembahasan :
Setiap warna akan dibagi sama banyak, maka jumlah kalung terbanyak adalah FPB dari jumlah 3 jenis manik-manik.
Faktorisasi prima
48=2⁴ x 3
60=2² x 3 x 5
72=2³ x 3²
FPB= 2² x 3=12 kalung
Jawaban : B
A. 24
B. 30
C. 48
D. 60
Pembahasan :
Kedua pohon akan sejajar lagi jika kelipatan jaraknya sama, yaitu KPKnya.
Faktorisasi prima
12= 2² x 3
15=3 x 5
KPK= 2² x 3 x 5=60 m
Jawaban : D
Baca juga : Soal Cerita FPB dan KPK
24. Untuk sebuah pesta, akan dibuat rangkaian bunga untuk hiasan. Panitia mempunyai menyiapkan 48 tangkai bunga matahari, 64 bunga lili dan 80 bunga mawar. Setiap rangkaian bunga terdiri dari kombinasi bunga yang sama. Jika dibuat rangkaian terbanyak yang bisa dibuat, berapa jumlah kombinasi bunga tiap rangkaian?
A. 3 bunga matahari, 6 bunga lili dan 5 bunga mawar
B. 3 bunga matahari, 4 bunga lili dan 5 bunga mawar
C. 4 bunga matahari, 6 bunga lili dan 5 bunga mawar
D. 4 bunga matahari, 8 bunga lili dan 5 bunga mawar
Pembahasan :
Setiap jenis bunga akan dibagi sama banyak, maka jumlah rangkaian terbanyak adalah FPB dari jumlah 3 jenis bunga.
Faktorisasi prima
48=2⁴ x 3
64=2⁶
80= 2⁴ x 5
FPB= 2⁴=16
Rangkaian bunga yang dapat dibuat adalah 16 buah.
Jumlah bunga dalam tiap rangkaian :
Bunga matahari=48 : 16=3 tangkai
Bunga lili=64 : 16=4 tangkai
Bunga mawar=80 : 16=5 tangkai
Jawaban : B
25. Arya mengunjungi perpustakaan setiap 6 hari sekali, Banu ke perpustakaan setiap 9 hari sekali dan Cahyo setiap 12 hari sekali. Pada tanggal 25 Februari 2020 mereka bersama-sama ke perpustakaan. Pada tanggal berapa mereka akan bersama-sama ke perpustakaan lagi?
A. 30 Maret 2020
B. 31 Maret 2020
C. 1 April 2020
D. 2 April 2020
Pembahasan :
Untuk menentukan waktu mereka akan bersama-sama lagi adalah dengan menghitung KPK.
Faktorisasi prima
6=2 x 3
9=3²
12= 2² x 3
KPK= 2² x 3²=36
Mereka akan ke perpustakaan bersama-sama lagi 36 hari setelah 25 Februari 2020. Ingat, tahun 2020 adalah tahun kabisat sehingga jumlah hari pada bulan Februari ada 29.
Pertama, jumlahkan 25 (dari 25 Februari) dengan 36 (KPK)
25 + 36=61
Lalu kurangi dengan jumlah hari pada bulan Februari 2020.
61 - 29=32
Karena tidak ada tanggal 32, maka kurangi dengan jumlah hari pada bulan Maret yaitu 31
32 - 31=1
Maka mereka akan ke perpustakaan bersama-sama lagi pada tanggal 1 April 2020.
Jawaban : C
Baca juga Soal Latihan Ujian Sekolah IPA SD
Demikian soal-soal latihan tentang Bilangan Bulat untuk Kelas 6 SD. Semoga bermanfaat untuk lebih memahami.