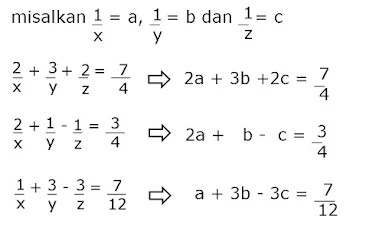Baca juga : Sistem Persaman Linear Dua Variabel
Sama seperti sistem persamaan linear dua variabel (spldv), sistem persamaan linear tiga variabel (spltv) juga memiliki nilai penyelesaian. Kita dapat menentukan penyelesaiannya dengan metode substitusi, metode eliminasi ataupun gabungan metode substitusi dan eliminasi.
Apa yang dimaksud dengan sistem tiga persamaan linear?
Secara umum, solusi sistem dalam tiga variabel adalah triple terurut (x, y, z) yang membuat SEMUA TIGA persamaan benar. Dengan kata lain, itulah kesamaan yang dimiliki ketiganya
Apa rumus dari 3 persamaan fungsi linier?
Rumus fungsi liniernya adalah: y = mx + b (bentuk perpotongan kemiringan) y−y1=m(x−x1) y − y 1 = m ( x − x 1 ) (bentuk kemiringan titik) Ax + By = C (bentuk standar)
Bagaimana cara menyelesaikan sistem persamaan linear dengan 3 variabel?
Sistem tiga persamaan dalam tiga variabel dapat diselesaikan dengan menggunakan serangkaian langkah yang memaksa variabel untuk dihilangkan. Langkah-langkahnya termasuk menukar urutan persamaan, mengalikan kedua sisi persamaan dengan konstanta bukan nol, dan menambahkan kelipatan bukan nol dari satu persamaan ke persamaan lainnya.
Berikut kami sajikan soal-soal spltv untukmu berlatih. Semoga dapat membantumu agar dapat lebih memahami materi ini.
1. Penyelesaian dari sistem persamaan linear 3x + 4y + z=5 ; x + 2y - z=-3 ; 2x + 3y + 2z=7 adalah{(x,y,z)}. Nilai dari x adalah....
A. -1
B. 1
C. 2
D. 3
Pembahasan :
Persamaan 1 dan 2, eliminasi nilai z
3x + 4y + z=5
x + 2y - z=-3 +
4x + 6y =2 ........ (4)
Persamaan 2 dan 3, juga eliminasi nilai z
x + 2y - z=-3 | x 2 |
2x + 3y + 2z=7 | x 1 |
2x + 4y - 2z=-6
2x + 3y + 2z=7 +
4x + 7y =1 ........(5)
Persamaan 4 dan 5, eliminasi nilai y
4x + 6y=2 | x 7 |
4x + 7y=1 | x 6 |
28x + 42y=14
24x + 42y= 6 +
4x =8
x =8 : 4=2
Jawaban : C
2. Jika penyelesaian persamaan linear berikut adalah{(x₀,y₀,z₀)}, tentukan nilai dari x₀ + y₀ + z₀ !
3x + y + z=-2
2x + 3y - z=12
2y + 3z=7
A. 0
B. 2
C. 5
D. 7
Pembahasan :
Karena pada persamaan (3) tidak ada nilai x, maka persamaan (1) dan (2) kita eliminasi nilai x nya
3x + y + z=-2 | x 2 |
2x + 3y - z=12 | x 3 |
6x + 2y + 2z=-4
6x + 9y - 3z=36 -
-7y + 5z=-40 ..... (4)
Persamaan (3) dan (4), eliminasi nilai z
2y + 3z=7 | x 5 |
-7y + 5z=-40 | x 3 |
10y + 15z=35
-21y + 15z=-120 -
31y =155
y =155 : 31=5
substitusi nilai y ke persamaan (3)
2y + 3z=7
2(5) + 3z=710 + 3z=7
3z=7-10
z=-3 : 3=-1
substitusi nilai y dan z ke persamaan (2)
2x + 3y - z=12
2x +3(5) - (-1)=12
2x + 15 + 1=12
2x =12 - 16
x =-4 : 2=-2
x₀ + y₀ + z₀=-2 + 5 + (-1)
=2
Jawaban : B
3. Sistem persamaan linear x + 6y + z = 2 ; 2x + 3y = 2 ; 4x - 2z = 3 mempunyai penyelesaian{(x,y,z)}. nilai dari 12xy=....
A. -2
B. -1
C. 1
D. 2
Pembahasan :
x + 6y + z=2 .....(1)
2x + 3y=2..........(2)
4x - 2z=3..........(3)
Eliminasi nilai y dari persamaan (1) dan (2)
x + 6y + z=2 | x 1 |
2x + 3y =2 | x 2 |
x + 6y + z=2
4x + 6y =4 -
- 3x + z=-2..... (4)
Eliminasi nilai z dari persamaan (3) dan (4)
4x - 2z=3 |x1|
-3x + z =-2 |x2|
4x - 2z=3
-6x + 2z=-4 +
-2x =-1
x =½
4x - 2z=3
4(½) - 2z=3
2 - 2z=3
- 2z=3 - 2
z=1 : -2
=-½
2x + 3y=2
2(½) + 3y=2
3y=2 - 1
3y=1
y=⅓
12xy=12 (½) (⅓)
=2
Jawaban : D
4. Perhatikan sistem persamaan linear tiga variabel berikut :
2x - y + z = 0
x + y - z = 9
3x - 2y - 2z = 5
Maka penyelesaiannya adalah...
A. x=3, y=2, z=5
B. x=3, y=4, z=-2
C. x=3, y= 4, z=2
D. x=2, y=8, z=3
Pembahasan :
2x - y + z=0
x + y - z=9 +
3x =9
x=9 : 3 =3
x + y - z=9 | x2 |
3x - 2y - 2z=5 | x1 |
2x + 2y - 2z=18
3x - 2y - 2z= 5 +
5x - 4z=23
5(3) - 4z=23
-4z=23 - 15
z=8 : -4
z= -2
x + y - z=9
3 + y – (-2)=9
y = 9 - 3 - 2
y = 4
Jawaban : B
5. Jika diketahui x + y=4, x + z=3 dan y - 2z=-3, maka nilai dari xyz adalah....
A. -20
B. -10
C. -5
D. 5
Pembahasan :
x + y=4
x + z=3 -
y - z=1
y - z=1
y - 2z=-3 -
z=4
x + z=3
x + 4=3
x =3 - 4=-1
x + y=4
-1 + y=4
y=4 + 1=5
Nilai xyz=(-1) (5) (4)=-20
Jawaban : A
6. Gambar di bawah menunjukkan berat beberapa buah. Jika buah dengan jenis yang sama dianggap memiliki berat yang sama, maka berat 5 buah apel adalah.... kg
A. 1 kg
B. 1,2 kg
C. 1,5 kg
D. 2 kg
Pembahasan :
3 apel + 4 jeruk=1,52 | x3 |
2 mangga + 3 jeruk=1,10 | x4 |
9 apel + 12 jeruk=4,56
8 mangga + 12 jeruk=4,40 -
9 apel - 8 mangga=0,16
2 apel + 3 mangga=1,23 | x8 |
9 apel - 8 mangga=0,16 | x3 |
16 apel + 24 mangga=9,84
27 apel - 24 mangga=0,48 +
43 apel =10,32
1 apel = 0,24
5 apel=5 x 0,24 kg=1,2 kg
Jawaban : B
7. Suatu bilangan terdiri dari tiga angka yaitu angka ratusan, puluhan dan satuan. Ketiga angka penyusunnya berjumlah 17, sedangkan angka ratusan dan puluhan jumlahnya 1 lebih banyak dari angka satuan. Jika angka satuan besarnya dua kali angka ratusan, maka tentukan bilangan tersebut!
A. 356
B. 458
C. 274
D. 346
Pembahasan :
Misalkan :
R =ratusan
P =puluhan
S =satuan
R + P + S=17 ... (1)
R + P=S + 1
R + P - S=1 ..... (2)
S=2R ...............(3)
Eliminasi persamaan (1) dan (2)
R + P + S=17
R + P - S= 1 -
2S=16
S=8
S=2R
8=2R
R=4
R + P + S=17
4 + P + 8=17
P =17 - 4 - 8
P =5
Bilangan tersebut adalah 458
Jawaban : B
9. Rata-rata tiga bilangan adalah 9. Jumlah bilangan pertama dan kedua besarnya 3 lebih banyak dari bilangan ketiga. Jumlah bilangan pertama dan ketiga besarnya 11 lebih besar dari bilangan kedua. Bilangan-bilangan tersebut adalah...
A. 6, 9 dan 12
B. 7, 8 dan 12
C. 5, 8 dan 14
D. 7, 9 dan 11
Pembahasan :
A + B + C=9 x 3
A + B + C=27 ...... (1)
A + B=C + 3
A + B - C=3 .........(2)
A + C=B + 11
A - B + C=11 ........(3)
Eliminasi persamaan (1) dan (2)
A + B + C=27A + B - C= 3 -
2C=24
C=12
Eliminasi persamaan (2) dan (3)
A + B - C= 3
A - B + C=11 +
2A =14
A =7
Substitusi ke persamaan (1)
A + B + C =27
7 + B + 12=27
B =27 - 7 - 12
=8
Jawaban : B
10. Sebuah fungsi kuadrat f(x) mempunyai nilai f(0)=3, f(1)=6 dan f(-2)=-17. Tentukan fungsi kuadrat tersebut!
A. f(x)=-x² + 4x + 3
B. f(x)=x² + 4x + 3
C. f(x)=-x² - 4x + 3
D. f(x)=-x² + 4x - 3
Pembahasan :
Persamaan umum fungsi kuadrat
f (x)=ax² + bx + c
f(0)=a(0)² + b(0) + c
3=0 + 0 + c
3=c
f(1)=a(1)² + b(1) + c
6=a + b + 3
3=a + b..........(1)
f(-2)=a(-2)² + b(-2) + c
-9=4a - 2b + 3
-12=4a - 2b...... (2)
Eliminasi persamaan (1) dan (2)
a + b= 3 | x2 |
4a - 2b=-12 | x1 |
2a + 2b= 6
4a - 2b=-12 +
6a =-6
a =-1
a + b=3
-1 + b=3
b=4
Fungsi kuadratnya adalah f(x)=-x² + 4x + 3
Jawaban : A
11. Arman, Candra dan Ervan pergi ke toko buku bersama-sama dan membeli alat tulis dengan merk yang sama. Arman membeli sebuah pensil, sebuah buku dan sebuah pulpen. Ia harus membayar sebesar Rp 13.000,00. Candra membayar Rp 21.500,00 untuk pembelian dua buah pensil, dua buah buku dan sebuah pulpen. Ervan membayar Rp 27.500,00 untuk pembelian sebuah pensil, 3 buah buku dan 2 buah pulpen. Berapakah harga 3 buah pensil, sebuah buku dan sebuah pulpen?
A. Rp 20.000,00
B. Rp 21.500,00
C. Rp 25.000,00
D. Rp 26.500,00
Pembahasan :
pensil=x
buku=y
pulpen=z
Arman : x + y + z=13.000
Candra : 2x + 2y + z=21.500
Ervan : x + 3y + 2z=27.500
x + y + z=13.000 |x2|
2x + 2y + z=21.500 |x1|
2x + 2y + 2z=26.000
2x + 2y + z=21.500 -
z= 4.500
x + y + z=13.000 |x3|
x + 3y + 2z=27.500 |x1|
3x + 3y + 3z=39.000
x + 3y + 2z=27.500 -
2x + z =11.500
2x + 4.500 =11.500
2x =7.000
x =3.500
x + y + z=13.000
3.500 + y + 4.500=13.000
y =13.000 - 8.000
=5.000
3x + y + z=3(3.500) + 5.000 + 4.500
=10.500 + 9.500
=20.000
Jawaban : A
12. Tiga tahun yang lalu jumlah umur Ami, Rahma dan Zahra adalah 38 tahun. Jumlah umur Ami dan Rahma sekarang lebih besar 5 tahun dari umur Zahra. Tiga tahun yang akan datang, umur Zahra dua kali umur Ami. Berapakah umur Rahma sekarang?
A. 12
B. 13
C. 15
D.17
Pembahasan :
Tiga tahun yang lalu jumlah umur Ami, Rahma dan Zahra adalah 38 tahun
⇒ (A-3) + (R-3) + (Z-3)=38
A + R + Z=47.... (1)
Jumlah umur Ami dan Rahma sekarang lebih besar 5 tahun dari umur Zahra
⇒ A + R=Z + 5
A + R - Z=5......(2)
Tiga tahun yang akan datang, umur Zahra dua kali umur Ami
⇒ Z + 3=2 (A+3)
Z + 3=2A + 6
Z=2A + 3.......(3)
Eliminasi (1) dan (2)
A + R + Z=47
A + R - Z= 5 -
2Z=42
Z=21
Substitusi (3)
Z =2A + 3
21=2A + 3
21 - 3=2A
18=2A
A=9
A + R - Z=5
9 + R - 21=5
R =5 + 21 - 9
R =17
Jawaban : D
13. Bu Rina, Bu Asih dan Bu Yanti belanja di toko sembako yang sama. Bu Rina membayar Rp 45.000,00 untuk pembelian 2 kg beras, 1 kg gula pasir dan 1 kg minyak sayur. Bu Asih membayar Rp 47.000,00 untuk pembelian 1 kg beras, 2 kg gula pasir dan 1 kg minyak sayur. Bu Yanti membeli 3 kg beras dan 1 kg gula pasir lalu membayar Rp 42.000,00. Ibu akan membeli 3 kg gula pasir untuk membuat kue. Jika ibu membayar dengan selembar uang lima puluhan ribu, berapa uang kembalian yang ibu terima?
A. Rp 10.000,00
B. Rp 12.000,00
C. Rp 13.000,00
D. Rp 14.000,00
Pembahasan :
Bu Rina : 2b + g + m=45.000
Bu Asih : b + 2g + m=47.000
Bu Yanti : 3b + g =42.000
2b + g + m=45.000
b + 2g + m=47.000 -
b - g =-2.000
3b + g=42.000
b - g=-2.000 +
4b =40.000
b =10.000
b - g=- 2.000
10.000 - g=-2.000
10.000 + 2.000=g
g=12.000
Ibu membeli 3 kg gula pasir=3 (12.000)
=36.000
Uang kembalian=50.000 - 36.000
=Rp 14.000,00
Jawaban : D14. Diketahui sistem persamaan linear tiga variabel berikut :
Himpunan penyelesaiannya adalah...
A.{(3,4,5)}
B.{(3,5,6)}
C.{(3,4,6)}
D.{(4,5,6)}
Pembahasan :
2a + 3b + 2c=7/4
2a + b - c=3/4 -
2b + 3c=1
2a + 3b + 2c=7/4 |x1|
a + 3b - 3c=7/12 |x2|
2a + 3b + 2c=7/4
2a + 6b - 6c=7/6 -
- 3b + 8b=7/12
2b + 3c=1 |x8|
-3b + 8b=7/12 |x3|
16b + 24c=8
-9b + 24c=7/4 -
25b =25/4
b =1/4
1/y =1/4
maka y=4
2b + 3c=1
2(1/4) + 3c=1
1/2 + 3c=1
3c=1 - 1/2
c=1/2 : 3
c=1/6
1/z=1/6
maka z=6
a + 3b - 3c=7/12
a + 3/4 - 3/6=7/12
a =7/12 - 3/4 + 3/6
a =1/3
1/x =1/3
x=3
Jawaban : C
15. Diketahui sistem persamaan linear tiga variabel berikut :
Penyelesaian sistem persamaan linear tersebut adalah...
A.{(-1, 3, 5)}
B.{(3, 5, -1)}
C.{(5, 3, -1)}
D.{(-1, 5, 3)}
Pembahasan :
2p + q - r=3/20
3p - 2q + r=3/5 +
5p - q =15/20
2p + q - r=3/20 | x2 |
2p - 3q + 2r=13/20 | x1 |
4p + 2q - 2r=6/20
2p - 3q + 2r=13/20 +
6p - q =19/20
6p - q=19/20
5p - q=15/20 -
p =1/5
1/x+2=1/5
maka x + 2=5
x =3
5p - q=15/20
1 - q=3/4
q=1/4
1/y-1 =1/4
maka y - 1=4
y =5
3p - 2q + r=3/5
3/5 - 1/2 + r=3/5
r=1/2
1/z+3=1/2
maka z + 3=2
z =-1
Jawaban : B
1 - q=3/4
q=1/4
1/y-1 =1/4
maka y - 1=4
y =5
3p - 2q + r=3/5
3/5 - 1/2 + r=3/5
r=1/2
1/z+3=1/2
maka z + 3=2
z =-1
Jawaban : B
0,5 P + 0,2 Q + 0,3 R=-0,1
0,2 P + 0,6 Q - 0,1 R=1,9
0,5 P - 0,1 Q + 0,4 R=-1,3
Nilai dari 0,2PQR adalah....
A. -1,2
B. -3
C. -12
D. -15
Pembahasan :
0,5 P + 0,2 Q + 0,3 R=-0,1 | x2 |
0,2 P + 0,6 Q - 0,1 R=1,9 | x5 |
P + 0,4 Q + 0,6 R=-0,2
P + 3,0 Q - 0,5 R= 9,5 -
- 2,6 Q + 1,1 R=-9,7
0,5 P + 0,2 Q + 0,3 R=-0,1
0,5 P - 0,1 Q + 0,4 R=-1,3 -
0,3 Q - 0,1 R=1,2
-2,6 Q + 1,1 R=-9,7 | x1 |
0,3 Q - 0,1 R=1,2 | x11|
-2,6 Q + 1,1 R=-9,7
3,3 Q - 1,1 R=13,2 +
0,7 Q =3,5
Q =5
0,3 Q - 0,1 R=1,2
0,3 (5) - 0,1 R=1,2
1,5 - 0,1 R=1,2
1,5 - 1,2 =0,1 R
0,3=0,1 R
R=3
0,2 P + 0,6 Q - 0,1 R=1,9
0,2 P + 0,6(5) - 0,1(3)=1,9
0,2 P + 3 - 0,3=1,9
0,2 P =1,9 + 0,3 - 3
0,2 P =- 0,8
P =- 4
Jawaban : C
A. Rp 350.000,00
B. Rp 400.000,00
C. Rp 500.000,00
D. Rp 650.000,00
Pembahasan :
Jumlah uang A, B dan C adalah Rp 2.200.000,00
A + B + C=2.200.000
Jika A memberikan Rp 50.000,00 uangnya kepada C, maka jumlah uang A sama dengan C
A - 50.000=C + 50.000
A - C=100.000
Jika uang B ditambah Rp 600.000,00 maka besarnya sama dengan jumlah uang A dan C
B + 600.000=A + C
600.000=A - B + C
A + B + C=2.200.000
A - B + C= 600.000 +
2A + 2C=2.800.000
A + C=1.400.000
A + C=1.400.000
A - C= 100.000 -
2C=1.300.000
C= 650.000
Jawaban : D
18. Di suatu lapangan, tarif parkir untuk sepeda motor adalah Rp 2.000,00, mobil Rp 5.000,00 dan bus Rp 10.000,00. Banyaknya sepeda motor yang parkir di lapangan tersebut adalah dua kali jumlah mobil dan bus. Banyaknya mobil adalah ⅓ jumlah sepeda motor dan bus. Jika hasil tarif parkir yang terkumpul adalah Rp 205.000,00 maka jumlah sepeda motor yang ada di lapangan parkir adalah....
A. 5
B. 15
C. 40
D. 50
Pembahasan :
Misalkan
motor=x
mobil=y
bus=z
x=2 (y + z)
⇒ x=2y + 2z.... (1)
y= ⅓ (x + z)
⇒ 3y=x + z ......(2)
2.000x + 5.000y + 10.000z=205.000 (sederhanakan dengan dibagi 1.000)
⇒2x + 5y + 10z=205 .... (3)
Substitusi (1) ke (2)
3y=x + z
3y=2y + 2z + z
3y - 2y=2z + z
y =3z..... (4)
Substitusi (1) ke (3)
2x + 5y + 10z=205
2(2y + 2z) + 5y + 10z=205
4y + 4z + 5y + 10z=205
9y + 14z=205
Substitusi persamaan (4)
9(3z) + 14z=205
27z + 14 z=205
41z =205
z =5
y=3z
=3(5)
=15
x=2y + 2z
=2(15) + 2(5)
=30 + 10
=40 sepeda motor
Jawaban : C
19. Diketahui segitiga ABC dengan sudut A, B dan C. Besar sudut B adalah dua kali besar sudut A, sedangkan besar sudut C 5 lebihnya dari sudut B. Berapakah besar sudut-sudut segitiga ABC tersebut?
A. 30°, 60° dan 90°
B. 45°, 90° dan 95°
C. 40°, 80° dan 85°
D. 35°, 70° dan 75°
Pembahasan :
Jumlah besar sudut segitiga=180°
A + B + C=180.... (1)
B=2A ..... (2)
C=B + 5 ..... (3)
Substitusi (2) ke (3)
C=2A + 5
A + B + C=180
A + 2A + 2A + 5=180
5A=180 - 5
A=175 : 5
A=35°
B=2A
=2(35)
=70°
C=B + 5
=70 + 5
=75°
Jawaban : D
20. Di dalam sebuah kantung terdapat 36 uang logam yang terdiri dari pecahan dua ratusan, lima ratusan dan seribuan. Jumlah nominal semua uang logam tersebut adalah Rp 22.400,00. Jika jumlah uang pecahan seribuan adalah dua kali jumlah uang pecahan lima ratusan, berapa jumlah masing-masing uang logam di kantung tersebut?
A. 5, 8 dan 12
B. 6, 12 dan 15
C. 12, 8, dan 16
D. 8, 12 dan 16
Pembahasan :
Misalkan
Jumlah uang dua ratusan=x
Jumlah uang lima ratusan=y
Jumlah uang seribuan=z
x + y + z=36..... (1)
200x + 500y + 1.000z=22.400 (sederhanakan dengan dibagi 100)
2x + 5y + 10z=224.... (2)
z=2y ....... (3)
Karena pada persamaan (3) hanya ada variabel y dan z, maka eliminasi x dari (1) dan (2)
x + y + z= 36 |x2|2x + 5y + 10z=224 |x1|
2x + 2y + 2z= 72
2x + 5y + 10z=224 -
- 3y - 8z=-152
substitusi persamaan (3)
- 3y - 8(2y)=- 152
- 3y - 16y =- 152
- 19y=- 152
y=8
z=2y
z=16
x + y + z=36
x + 8 + 16=36
x=36 - 8 - 16
x=12
Jumlah uang dua ratusan=12
Jumlah uang lima ratusan= 8
Jumlah uang seribuan=16
Demikian soal latihan tentang Sistem Persamaan Linear Tiga Variabel beserta pembahasannya. Semoga bermanfaat