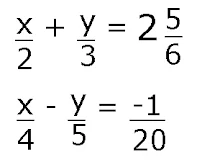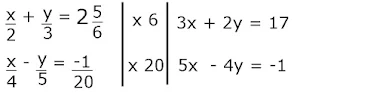Dibawah ini adalah soal latihan sistem persamaan linear dua variabel untuk kelas 8 berikut jawaban dan pembahasan agar lebih mudah dipahami.
Baca juga : Sistem Persamaan Linear Dua Variabel
1. Berikut ini yang merupakan persamaan linear dua variabel adalah....
A. 3x - 5 = 7
B. 5y + 2x - 3xy=0
C. y=x² + 7x + 12
D. 4x + 3y=24
Pembahasan :
Persamaan linear dua variabel adalah persamaan yang memiliki dua variabel bebas dan setiap variabelnya berpangkat satu.
Jawaban : D
2. Diketahui persamaan (I) 2x + 5y =19 dan persamaan (II) y= 2x - 1. Jika persamaan (II) disubstitusi ke dalam persamaan (I) akan menghasilkan persamaan linear....
A. 2x + 5x - 1=19
B. 2x + 5 (2x - 1)=19
C. 2x + 5 (2x)=20
D. 7x=18
Pembahasan :
(I) 2x + 5y=19 dan (II) y=2x - 1
substitusi persamaan (II) ke dalam persamaan (I)
2x + 5y=19
2x + 5(2x - 1)=19
Jawaban : B
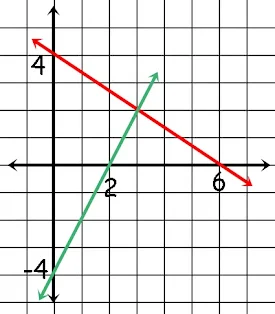
3. Perhatikan gambar berikut!
Grafik di atas merupakan penyelesaian dari persamaan .....
A. 4x=6y dan -4x=2y
B. 4x + 6y=0 dan -4x + 2y=0
C. 4x + 6y=24 dan -4x + 2y=-8
D. 4y + 6x=24 dan -4y + 2x=-8
Pembahasan :
Garis merah memotong sumbu y di (0,4) dan sumbu x di (6,0)
Persamaan : 4x + 6y=4.6
4x + 6y=24
Garis hijau memotong sumbu y di (0, -4) dan sumbu x di (2,0)
Persamaan : -4x + 2y=-4.2
-4x + 2y=-8
Jawaban : C
4. Grafik penyelesaian sistem persamaan 2x+ y=10 dan 4x + 3y=24 adalah....
Pembahasan :
Titik potong persamaan 2x + y=10 di sumbu x
➤ y=0, maka 2x=10
x=5
(5,0)
Titik potong persamaan 2x + y=10 di sumbu y
➤ x=0, maka y=10
(0,10)
Titik potong persamaan 4x + 3y=24 di sumbu x
➤ y=0, maka 4x=24
x=6
(6,0)
Titik potong persamaan 4x + 3y=24 di sumbu y
➤ x=0, maka 3y=24
y=8
(0,8)
Jawaban : D
Baca juga : Gradien Dan Persamaan Garis Lurus
5. Penyelesaian sistem persamaan 2x + 3y=7 dan x + y=4 adalah...
A. (2,1)
B. (5,-1)
C. (-1,3)
D. (1,3)
Pembahasan :
Jawaban : B
6. Nilai x yang memenuhi sistem persamaan linear x + 3y=7 dan 3x + y=-3 adalah...
A. -2
B. -1
C. 1
D. 2
Pembahasan :
Jawaban : A
Nilai 3x - 2y adalah....
A. 2
B. 12
C. 22
D. 32
Pembahasan :
Jawaban : C
8. Jika diketahui x + 3y=1 dan -2x + 5y=20, maka nilai dari x.y adalah,,,
A. - 10
B. - 3
C. 3
D. 10
9. Jika diketahui sistem persamaan linier berikut :
Tentukan nilai dari ½xy!
A. -3
B. 3
C. 6
D. 12
Pembahasan :
Masing-masing persamaan dikalikan KPK dari penyebut agar tidak berbentuk pecahan
Lakukan perhitungan seperti biasa, menggunakan salah satu metode yang dikuasai
Jawaban : C
10. Jika p dan q adalah penyelesaian dari sistem persamaan 2(p+1) - 5(q-3)=23 dan 3(p+1) + 2(q-3)=6, maka nilai p + q=....
A. 0
B. 1
C. 2
D. 3
Pembahasan :
Misalkan a=p+1 dan b=q-3, maka sistem persamaannya menjadi
2a - 5b=23 dan 3a + 2b=6
p + q=3 + 0=3
Jawaban : D
A. 2x - 3y=25.000 dan x - 5y=23.000
B. 2x + 3y=25.000 dan x + 5y=23.000
C. 2x + 3y=25.000 dan x=5y + 23.000
D. 2x=25.000 + 3y dan x=25.000 - 5y
Pembahasan :
misalkan buku=x dan pensil=y
2 buku dan 3 pensil=Rp 25.000,00
➤ 2x + 3y=25.000
1 buku dan 5 pensil =Rp 23.000,00
➤ x + 5y=23.000
Jawaban : B
12. Jumlah umur Bima dan Duta sekarang adalah 21 tahun. Enam tahun yang akan datang, Umur Bima dua kali umur Duta. Jika umur Bima dimisalkan dengan b dan umur Duta dimisalkan dengan d, model matematika yang tepat untuk pernyataan tersebut adalah....
A. b + d=21 ; b + 6=2d
B. b - d=21 ; b + 6=2d
C. b + d=21 ; b + 6=2d + 6
D. b + d=21 ; b + 6=2 (d + 6)
Pembahasan :
Misal umur Bima=b dan umur Duta=d
Jumlah umur Bima dan umur Duta=21 tahun
➤ b + d=21
Enam tahun yang akan datang umur Bima dua kali umur Duta
Ingat !! Enam tahun yang akan datang umur Bima bertambah 6 dan umur Duta bertambah 6
➤ b + 6=2 (d + 6)
Jawaban : D
13. Keliling sebuah persegi panjang adalah 46 cm. Jika panjangnya lebih 8 cm dari lebarnya, maka model matematika yang tepat untuk soal di atas adalah....
A. p x l=46 dan p + l=8
B. p x l=46 dan p=l + 7
C. p + l=46 dan p=l + 7
D. 2p + 2l=46 dan p=l + 7
Pembahasan :
Misalkan panjang=p dan lebar=l
Keliling sebuah persegi panjang adalah 46 cm
Rumus keliling persegi panjang adalah 2 x (p+l)=2p + 2l
➤ 2p + 2l=46
Panjangnya lebih 8 cm dari lebarnya
➤ p=l + 7
Jawaban : D
14. Arya, Bima dan Candra pergi ke toko bersama-sama. Arya membayar Rp 28.000,00 untuk pembelian 2 pensil dan 4 pulpen. Bima membayar Rp 19.500,00 untuk pembelian sebuah pensil dan 3 pulpen. Jika Candra hanya membeli 5 buah pensil, berapa harga yang harus ia bayar?
A. Rp 5.000,00
B. Rp 12.500,00
C. Rp 15.000,00
D. Rp 17.500,00
Pembahasan :
Misal pensil=x dan pulpen=y
Arya ➤ 2x + 4y=28.000
Bima ➤ x + 3y=19.500
Candra ➤ 5x=?
5x=5 x 3.000
=Rp 15.000,00
Jawaban : C
15. Jumlah dua bilangan cacah adalah 61 sedangkan selisihnya 11. Hasil kali bilangan tersebut adalah....
A. 671
B. 900
C. 951
D. 1021
Pembahasan :
Misalkan bilangan-bilangan tersebut p dan q
Jumlah dua bilangan=61
➤ p + q=61
Selisih dua bilangan=11
➤ p - q=11
p + q=61
p - q=11 -
2q=50
q=25
p + q=61
p - q=11 +
2p =72
p =36
Hasil kali kedua bilangan=25 x 36=900
Jawaban : B
16. Bu Ana membeli 1 kg apel dan 3 kg mangga lalu membayar Rp 46.000,00. Di tempat yang sama Bu Rika membeli 2 kg apel dan 2 kg mangga dengan harga Rp 52.000,00. Berapa harga yang harus dibayar jika Bu Sinta membeli 3 kg apel dan 1 kg mangga?
A. Rp 56.000,00
B. Rp 58.000,00
C. Rp 60.000,00
D. Rp 62.000,00
Pembahasan :
Misalkan apel=a dan mangga=b
1 kg apel dan 3 kg mangga=Rp 46.000,00
➤ a + 3b=46.000
2 kg apel dan 2 kg mangga=Rp 52.000,00
➤ 2a + 2b=52.000
a + 3b=46.000 [ x 2]
2a + 2b=52.000 [ x 1]
2a + 6b=92.000
2a + 2b=52.000 -
4b=40.000
b=10.000
a + 3b=46.000
a + 3(10.000)=46.000
a=46.000 - 30.000
a=16.000
3 kg apel dan 1 kg mangga=3(16.000) + 10.000
=48.000 + 10.000
=58.000
Jawaban : B
17. Sebuah persegi panjang mempunyai keliling 74 cm. Lebarnya 7 cm kurang dari panjangnya. Berapa luas persegi panjang tersebut?
A. 220 cm²
B. 330 cm²
C. 385 cm²
D. 540 cm²
Pembahasan :
Keliling=2p + 2l=74
Lebar kurang 7 dari panjang
l=p - 7
2p + 2l=74
2p + 2(p - 7)=74
2p + 2p - 14=74
4p =74 + 14
4p =88
p =88 : 4
p =22 cm
l=p - 4
=22 - 7
=15 cm
Luas=p x l
=22 x 15
=330 cm²
18. Umur Ayah 3 kali umur Anwar. Jika jumlah umur mereka adalah 64 tahun, berapa umur Anwar tiga tahun yang akan datang ?
A. 16 tahun
B. 17 tahun
C. 18 tahun
D. 19 tahun
Pembahasan :
Misal umur Ayah=x dan umur Anwar=y
➤ x=3y
➤ x + y=64
3y + y=64
4y =64
y =64 : 4
y =16
Umur Anwar tiga tahun yang akan datang=16 + 3=19 tahun
Jawaban : D
19. Selisih umur Ibu dan Farah adalah 22 tahun. Delapan tahun yang akan datang, umur Ibu adalah dua kali umur Farah. Berapa umur Farah 4 tahun yang lalu?
A. 10 tahun
B. 14 tahun
C. 16 tahun
D. 18 tahun
Pembahasan :
Misal umur Ibu=x dan umur Farah=y
Selisih umur Ibu dan Farah=22
➤ x - y=22
Delapan tahun yang akan datang, umur Ibu adalah dua kali umur Farah
➤ x + 8=2 (y + 8)
x + 8=2y + 16
x - 2y=16 - 8
x - 2y=8
x - y=22
x - 2y=8 -
y=14
Umur Farah 4 tahun yang lalu
14 - 4=10 tahun
Jawaban : A
20. Di sebuah lapangan parkir terdapat 48 kendaraan yang terdiri dari sepeda motor dan mobil. Andi menghitung jumlah seluruh roda kendaraan yang ada di lapangan parkir itu ada 132 buah. Jika tarif parkir untuk sepeda motor Rp 1.000,00 dan untuk mobil Rp 2.500,00, berapa pendapatan biaya parkir di lapangan itu?
A. Rp 60.000,00
B. Rp 67.500,00
C. Rp 72.000,00
D. Rp 75.000,00
Pembahasan :
Misal sepeda motor=x dan mobil=y
Jumlah kendaraan=48
➤ x + y=48
Jumlah seluruh roda=132
Sebuah sepeda motor memiliki 2 roda dan sebuah mobil memiliki 4 roda
➤ 2x + 4y=132
x + y= 48 [x4]
2x + 4y=132 [x1]
4x + 4y=192
2x + 4y=132 -
2x = 60
x = 30
x + y=48
30 + y=48
y=48 - 30
y=18
Pendapatan parkir=1.000 x + 2.500 y
=1.000 (30) + 2.500 (18)
=30.000 + 45.000
=75.000
Jawaban : D
Demikian saol-soal latihan yang dapat kami berikan. Semoga dapat membantu untuk lebih mengerti materi Sistem Persamaan Linear Dua Variabel.