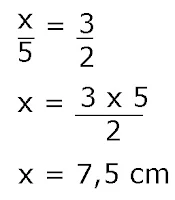Materi kongruen dan kesebangunan dipelajari di kelas 9. Berikut ini adalah soal-soal latihan beserta pembahasannya untukmu berlatih materi tersebut. Selamat mencoba !
1. Perhatikan gambar di bawah !
Segitiga ABC dan segitiga DEF adalah dua segitiga yang kongruen. Panjang DF adalah....
A. 5 cm
B. 6 cm
C. 7 cm
D. 8 cm
Pembahasan :
Sisi DF pada segitiga DEF adalah sisi di hadapan sudut yang bertanda ⦁, bersesuaian dengan sisi AB pada segitiga ABC. Maka DF=AB=7 cm
Jawaban : C
2. Diketahui ΔABC dan ΔDEF adalah kongruen. Jika AB=5 cm, BC=8 cm, AC=12 cm, EF=8 cm dan DF=5 cm, maka besar sudut yang sesuai adalah...
A. <A=<D, <B=<E dan <C=<F
B. <A=<E, <B=<D dan <C=<F
C. <A=<D, <B=<F dan <C=<E
D. <A=<F, <B=<E dan <C=<D
Pembahasan :
AB=DF=5cm, maka <C=<E
BC=EF=8 cm, maka <A=<D
AC=DE=12 cm, maka <B=<F
Jawaban : C
3. Perhatikan gambar di bawah !
A. 5 cm
B. 6 cm
C. 7 cm
D. 8 cm
Pembahasan :
Sisi DF pada segitiga DEF adalah sisi di hadapan sudut yang bertanda ⦁, bersesuaian dengan sisi AB pada segitiga ABC. Maka DF=AB=7 cm
Jawaban : C
2. Diketahui ΔABC dan ΔDEF adalah kongruen. Jika AB=5 cm, BC=8 cm, AC=12 cm, EF=8 cm dan DF=5 cm, maka besar sudut yang sesuai adalah...
A. <A=<D, <B=<E dan <C=<F
B. <A=<E, <B=<D dan <C=<F
C. <A=<D, <B=<F dan <C=<E
D. <A=<F, <B=<E dan <C=<D
Pembahasan :
AB=DF=5cm, maka <C=<E
BC=EF=8 cm, maka <A=<D
AC=DE=12 cm, maka <B=<F
Jawaban : C
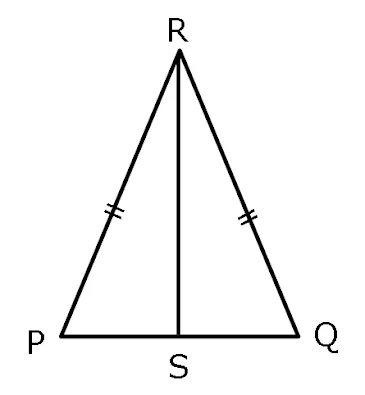
3. Perhatikan gambar di bawah !
PQR adalah segitiga sama kaki dengan PR=QR. Jika garis RS adalah garis bagi yang ditarik dari titik R, maka ΔPRS dan ΔQRS kongruen sesuai ketentuan....
A. sisi, sisi, sisi
B. sudut, sudut, sisi
C. sisi, sudut, sisi
D. sisi, sisi, sudut
Pembahasan :
- Sisi PR dan RS adalah kaki dari segitiga sama kaki PQR, maka PR=RS
- Garis bagi adalah garis yang membagi sudut sama besar. Garis RS adalah garis bagi, maka <PRS=SRQ
- Sisi RS adalah sisi yang digunakan bersama untuk segitiga PRS dan segitiga QRS
Jawaban : C
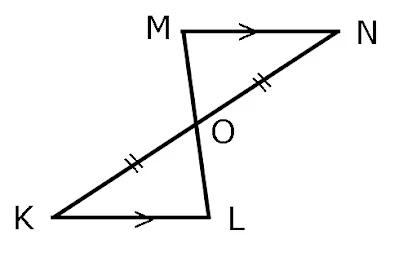
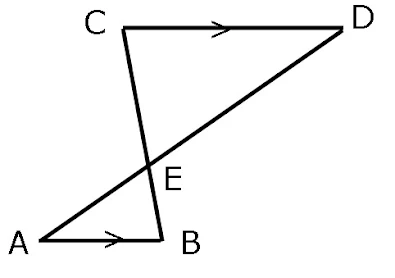
4. Pada gambar di bawah, garis KL sejajar dengan garis MN.
Maka ΔOKL kongruen dengan ΔOMN dengan ketentuan...
A. sisi, sisi, sisi
B. sudut, sudut, sisi
C. sisi, sudut, sisi
D. sudut, sisi, sudut
Pembahasan :
5. Perhatikan gambar berikut !
Pernyataan yang tidak benar tentang trapesium PQRS di atas adalah....
A. ΔPOS kongruen dengan ΔQOR
B. ΔPRS kongruen dengan ΔQRS
C. ΔPSQ kongruen dengan ΔQRP
D. ΔSOR kongruen dengan ΔPOQ
Jawaban : D
6. Pada gambar berikut, ΔACD dan ΔDBE adalah pasangan segitiga yang kongruen.
Panjang CE adalah....
A. 6 cm
B. 7 cm
C. 10 cm
D. 12 cm
Pembahasan :
AD=DE=5 cm
AC=BE=13 cm
Tentukan panjang CD dengan phytagoras
CD²=AC² - AD²
=13² - 5²
=169 - 25
=144
CD=√144
=12 cm
CE=CD - ED
=12 - 5
=7 cm
Jawaban : B
7. Perhatikan ukuran panjang sisi segitiga-segitiga berikut :
- ΔABC dengan AB=5 cm, AC=12 cm dan BC=13 cm
- ΔDEF dengan DE=7 cm, EF=24 cm dan DF=25 cm
- ΔKLM dengan KL=24 cm, LM=10 cm dan KM=26 cm
- ΔPQR dengan PQ=14 cm, PR=24 cm dan QR=20 cm
Pasangan segitiga yang sebangun adalah...
A. ΔABC dengan ΔDEF
B. ΔABC dengan ΔKLM
C. ΔDEF dengan ΔKLM
D. ΔKLM dengan ΔPQR
Pembahasan :
ΔABC dengan AB=5 cm, AC=12 cm dan BC=13 cm
ΔKLM dengan LM=10 cm KL=24 cm dan KM=26 cm
sehingga
Jawaban : B
8. Diketahui bangun datar-bangun datar berikut :
I. segitiga sama kaki
II. persegi panjang
III. persegi
IV. segitiga sama sisi
Bangun datar yang pasti sebangun adalah...
A. I dan II
B. I dan III
C. II dan III
D. III dan IV
Pembahasan :
Bangun datar yang pasti sebangun adalah bangun datar beraturan seperti persegi, segitiga sama sisi, lingkaran, segilima beraturan dan lain lain
Jawaban : D
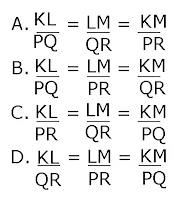
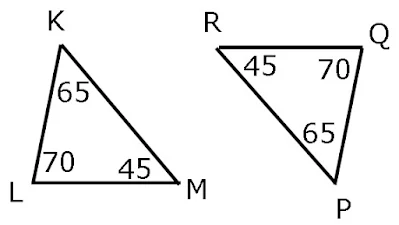
9. Diketahui segitiga KLM dan segitiga PQR dengan besar <K=65°, <L=70°, <P=65° dan <Q=45°. Jika segitiga-segitiga tersebut sebangun, maka pasangan sisi-sisi yang sebanding adalah....
Pembahasan :
Sisi-sisi yang sebanding adalah sisi-sisi yang diapit oleh sudut-sudut yang bersesuaian. Perhatikan gambar berikut !
Sisi KL diapit sudut 70° dan 60° begitu juga sisi PQ
Sisi LM diapit sudut 70° dan 45° begitu juga sisi QR
Sisi KM diapit sudut 65° dan 45° begitu juga sisi PR°
Jawaban : A
10. Diketahui segitiga ABC dengan panjang sisi AB=10 cm, BC=15 cm dan AC=20 cm serta segitiga PQR dengan panjang sisi PQ=12 cm, QR=8 cm dan PR=16 cm. Sudut yang sama besar adalah...
A. <A=<P, <B=<Q dan <C=<R
B. <A=<R, <B=<Q dan <C=<P
C. <A=<P, <B=<R dan <C=<Q
D. <A=<R, <B=<P dan <C=<Q
Pembahasan :
AB : BC : AC=10 : 15 : 20 (sederhanakan)
=2 : 3 : 4
QR : PQ : PR=8 : 12 : 16
=2 : 3 : 4
Sisi AB sebanding dengan sisi QR, maka <C=<P
Sisi BC sebanding dengan sisi PQ, maka <A=<R
Sisi AC sebanding dengan sisi PR, maka <B=<Q
Jawaban : B
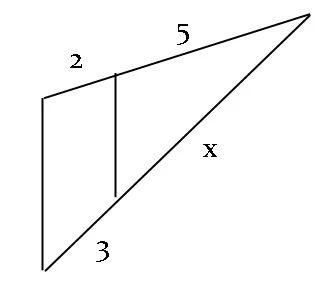
11. Perhatikan gambar berikut!
Nilai x adalah....
A. 6
B. 7,5
C. 8
D. 9
Pembahasan :
Jawaban : B
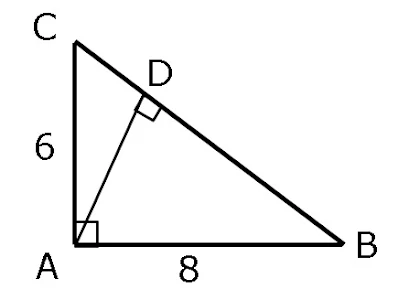
12. Perhatikan gambar berikut!
Tentukan panjang CD !
A. 12 cm
B. 13 cm
C. 14 cm
D. 16 cm
Pembahasan :
Jika segitiga ABC dan BDE kita uraikan akan menjadi seperti gambar di bawah.
Maka sisi-sisi yang sebandingnya adalah
10 =AB
5 12
AB= 10 x 12
5
=24 cm
CB²=AC² + AB²
=10² + 24²
=100 + 576
=676
CB=√676
=26 cm
CD=CB - DB
=26 - 12
=14 cm
Jawaban : C
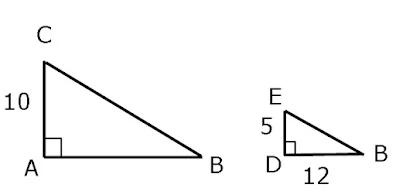
13. Perhatikan gambar berikut!
Tentukan panjang BD !
A. 3,6 cm
B. 4,8 cm
C. 5,4 cm
D. 6,4 cm
Pembahasan :
BC²=AB² + AC²
=8² + 6²
=64 + 36
=100
BC=√100=10 cm
AB²=BD x BC
8² =BD x 10
64 =BD x 10
BD=64 : 10
=6,4 cm
Jawaban : D
14. Perhatikan gambar berikut!
Tentukan panjang RS !
A. 6,72 cm
B. 7,2 cm
C. 8,32 cm
D. 9 cm
Pembahasan :
PQ²=PR² + RS²
=7² + 24²
=49 + 576
=625
PQ=√625=25 cm
RS=PR x QR
PQ
=7 x 24
25
=6,72 cm
Jawaban : A
15. Perhatikan dua trapesium siku-siku berikut !
Jika M dan N sebangun, tentukan luas N !
A. 174 cm²
B. 188,5 cm²
C. 274,5 cm²
D. 391,5 cm²
Pembahasan :
tM² =13²- (17-12)²
=169 - 25
=144
tM =12 cm
Perbandingan panjang sisi bangun M dan N adalah 12 : 18=2 : 3
tN =12 x 3
2
=18 cm
alasN = 17 x 3
2
=25,5 cm
Luas N =½ (18 + 25,5) x 18
=43,5 x 9
=391,5 cm²
Jawaban : D
16. Seorang anak berdiri pada jarak x meter dari sebuah tiang lampu yang tingginya 2,5 m. Tinggi anak itu adalah 150 cm dan terbentuk bayangan anak sepanjang 1,8 m akibat sinar lampu. Berapa jarak tempat anak berdiri dengan tiang lampu?
A. 0,8 m
B. 0,9 m
C. 1,0 m
D. 1,2 m
Pembahasan :
Perbandingan sisinya
1,8 + x =2,5
1,8 1,5
1,8 + x=2,5 x 1,8
1,5
1,8 + x=3,0
x=3,0 - 1,8
=1,2 m
Jawaban : D
17. Perhatikan gambar berikut!
Segitiga ABE sebangun dengan segitiga CED dimana sisi AB sejajar dengan CD. Jika AB=6 cm, BE=4 cm, EC=6 cm, CD=9 cm dan AD=17,5 cm, maka panjang ED adalah....
A. 7 cm
B. 7,5 cm
C. 10 cm
D. 10,5 cm
Pembahasan :
AB = AE = BE
CD ED CE
6 =AE
9 ED
⇒ AE : ED=6 : 9=2 : 3
AD=AE + ED=17,5 cm
ED= 3 x 17,5
2+3
=10,5 cm
Jawaban : D
18. Perhatikan gambar berikut !
ABCD adalah trapesium dan EF adalah garis di dalam trapesium yang sejajar dengan AB dan CD. Jika DE : AE=3 : 5, tentukan panjang EF !
A. 20 cm
B. 20,5 cm
C. 24 cm
D. 25,5 cm
Pembahasan :
Jawaban : B
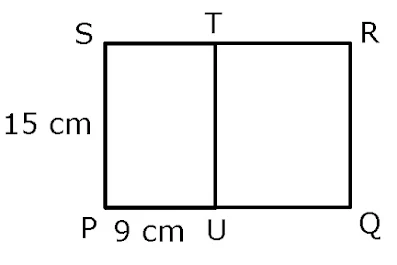
19. Perhatikan persegi panjang di bawah !
PQRS dan PUTS adalah dua persegipanjang yang sebangun. Luas TUQR adalah...
A. 240 cm²
B. 250 cm²
C. 280 cm²
D. 300 cm²
Pembahasan :
PQ =PS
SP ST
PQ =15
15 9
PQ=15 x 15
9
PQ=25 cm
Luas TUQR=Luas PQRS - Luas PTUS
=25 x 15 - 15 x 9
=375 - 135
=240 cm²
Jawaban : A
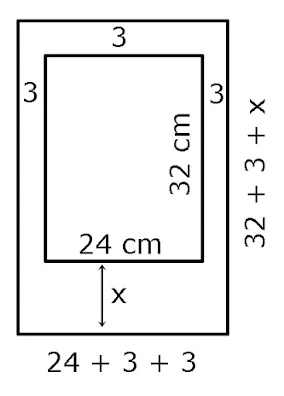
20. Sebuah foto berukuran 24 cm x 32 cm ditempelkan pada sebuah bingkai. Pada sisi kiri, atas dan kanan bingkai masih tersisa 3 cm. Jika foto dan bingkai sebangun, berapa sisa bingkai bagian bawah?
A. 4 cm
B. 5 cm
C. 6 cm
D. 7 cm
Pembahasan :
32 + 3 + x =32
24 + 3 + 3 24
35 + x =32
30 24
35 + x=30 x 32
24
35 + x=40
x=40 - 35
=5 cm
Jawaban : B
Demikian soal latihan kekongruenan dan kesebangunan yang dapat kami berikan. Semoga bermanfaat