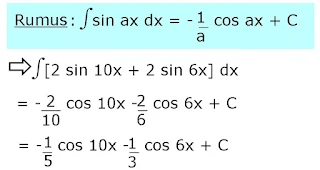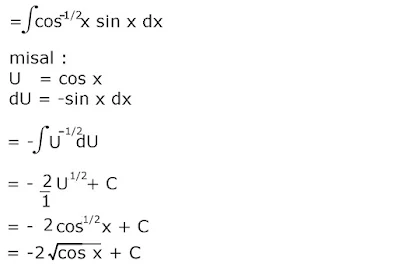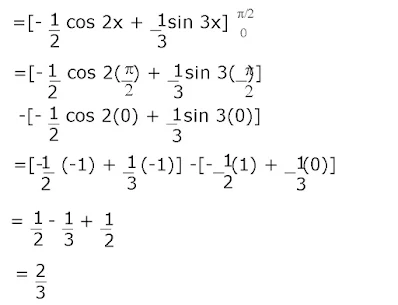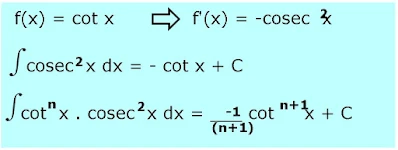Pada artikel ini kami akan berikan soal-soal latihan tentang integral trigonometri. Agar dapat menyelesaikan soal-soal integral trigonometri, selain rumus integral trigonometri kamu juga harus menguasai rumus-rumus turunan aljabar, turunan trigonometri, identitas trigonometri serta rumus jumlah sudut-sudut trigonometri. Perhatikan baik-baik pembahsan yang kami berikan, semoga membantumu memahami materi ini.
1. ∫ sin 4 x dx=
Pembahasan :
2. ∫(3 sin 6x + 2 cos 4x) dx=
Pembahasan :
3. ∫4 sin 8x cos 2x dx=
Pembahasan :
4 sin 8x cos 2x
=2. 2 sin 8x cos 2x
=2. [sin (8x+2x) + sin (8x - 2x)]
=2 [sin 10x + sin 6x]
=[2 sin 10x + 2 sin 6x]
4. ∫sin3x.cos x dx=
Pembahasan :
misal :
U =sin x
dU=cos x dx
⇒ ∫U3 du
=1 U4 + C
4
=1 sin4x + C
4
Pembahasan :
6 cos 12 x cos 3x
=3. 2 cos 12 x cos 3x
=3 [cos (12x+3x) + cos (12x-3x)]
=3 cos 15x + 3 cos 9x
6.

Pembahasan :
7.
Pembahasan :
=∫cos2x cos x dx
=∫(1 – sin2x) cos x dx
=∫(cos x – sin2x.cos x) dx
=∫cos x dx - ∫sin2x cos x dx
=sin x – 1/3 sin3x+ C
8. ∫ sin3x.cos2 x dx=
Pembahasan :
=∫ sin2x.sin x. cos2xdx
=∫ (1-cos2x) cos2x sinx dx
=∫ cos2x sin x – cos4x sinx dx
=- 1/3 cos3x+ 1/5 cos5x + C
Pembahasan :
10. ∫sin3 4x.cos5 4x dx=
Pembahasan :
=∫ sin2 4x.sin 4x. cos5 4x dx
=∫ ( 1 - cos2 4x) cos5 4x. sin 4x dx
=∫ ( cos5 4x. sin 4x – cos7 4x. sin 4x) dx

11.
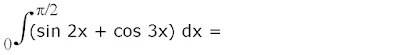
Pembahasan :
12. ∫ tan4 2x dx=
Pembahasan :
=∫tan2 2x . tan2 2xdx
=∫tan2 2x (sec2 2x-1)dx
=∫(tan2 2x.sec2 2x-tan2 2x) dx
=∫tan2 2x.sec2 2xdx - ∫tan2 2x dx
= 1 tan32x - ∫(sec2 2x-1) dx
3.2
= 1 tan3 2x - ∫sec2 2xdx +∫1dx
6
=1 tan3 2x – 1 tan2x + x + C
6 2
13. -15∫cosec6 x dx=
Pembahasan :
=-15∫cosec4 x. cosec2xdx
=-15∫[1 + cot2 x]2 cosec2 xdx
=-15∫[1 + 2 cot2 x + cot4x] cosec2 x dx
=-15∫[cosec2 x + 2 cot2xcosec2x + cot4x cosec2x] dx
=-15[-cot x – 2/3 cot3x– 1/5 cot5x] +C
=15 cot x + 10 cot3x + 3 cot5x+ C
14. ∫6x2 sin (x3 – 5)dx=
Pembahasan :
misal :
U =x3– 5
dU=3x2 dx
∫6x2 sin(x3 – 5) dx
=2∫sin U du
=- 2 cos U + C
=- 2 cos (x3 –5) + C
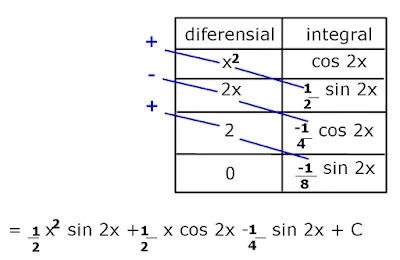
Pembahasan :
Cara cepat integral parsial
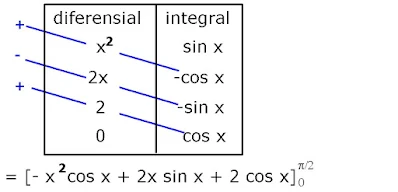
16. ∫(3x+1) sin x dx=
Pembahasan :
17.
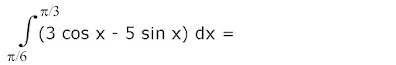
Pembahasan :
18. ∫sec4 x dx=
Pembahasan :
∫sec4 xdx
=∫sec2 x.sec2 x dx
=∫(tan2 x+ 1) sec2 x dx
=∫(tan2 x.sec2x + sec2 x) dx
=1/3tan3 x + tan x + C
19.

Pembahasan :
20.
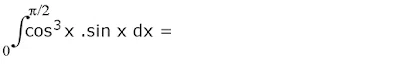
Pembahasan :