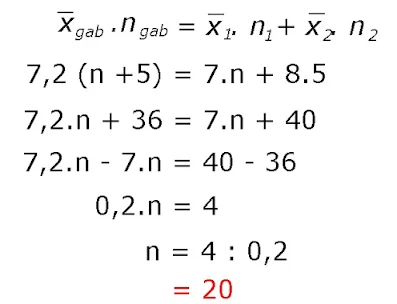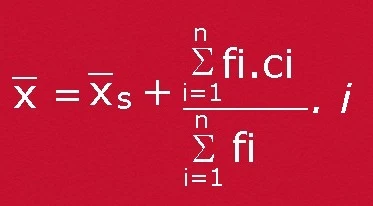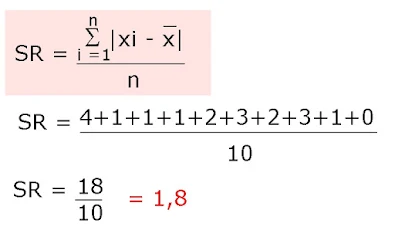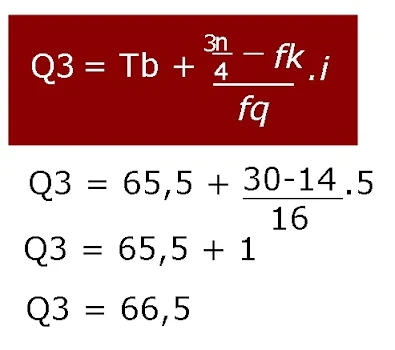Statistika adalah cabang dari ilmu matematika yang berhubungan dengan data. Dalam statistika kita mempelajari tentang pengumpulan penyusunan dan penganalisaan data.Berikut ini kami sajikan soal-soal latihan tentang statistika berupa ukuran pemusatan data maupun ukuran penyebaran data. Ukuran pemusatan data meliputi mean, median dan modus. Ukuran penyebaran data diantaranya jangkauan, simpangan kuartil dan simpangan baku. Semoga bermanfaat.
1. Soal Statistika Kelas 12 : Rata-rata hitung dari 3,4,5,5,6,7,7,8 adalah....
a. 5,25
b. 5,375
c.5,625
d.6,125
Pembahasan :
Rata-rata=3+4+5+5+6+7+7+8
8
=45
8
=5,625
2. Soal Statistika Kelas 12 : Hasil nilai ulangan Matematika di suatu kelas disajikan dalam tabel frekuensi berikut. Jika rata-rata nilai ulangan itu adalah 83,5 maka nilai p adalah...
 |
| Soal Statistika Kelas 12 gambar 1 |
a. 2
b. 3
c. 4
d. 5
Pembahasan :
3. Soal Statistika Kelas 12 : Tabel berikut adalah hasil ulangan di suatu kelas.
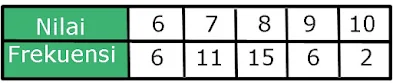 |
| Soal Statistika Kelas 12 gambar 2 |
Seorang siswa harus mengikuti remedial jika nilainya lebih kecil dari nilai rata-rata kelas. Berapa siswa yang harus mengikuti remedial?
a. 15 orang
b. 17 orang
c. 21 orang
d. 23 orang
Pembahasan :
Yang mengikuti remedial adalah yang nilainya di bawah 7,675, maka yang mempunyai nilai 6 dan 7 yaitu ada 6+11=17 orang
4. Soal Statistika Kelas 12 : Rata-rata nilai ulangan di suatu kelas adalah 7. Jika digabungkan dengan nilai 5 orang siswa lain yang rata-ratanya 8 maka nilai rata-ratanya menjadi 7,2. Berapa jumlah siswa pada kelompok pertama?
a. 20
b. 24
c. 25
d. 30
Pembahasan :
5. Soal Statistika Kelas 12 : Rata-rata tinggi badan di klub voly adalah 172 cm dan rata-rata tinggi badan di klub basket adalah 177 cm. Jika tinggi kedua klub digabung, rata-ratanya menjadi 174 cm. Berapa perbandingan jumlah anggota klub voly dan basket?
a. 1:2
b. 1:3
c. 2:3
d. 3:2
Pembahasan :
6. Soal Statistika Kelas 12 : Hasil nilai ulangan ditunjukkan pada histogram berikut.
Nilai rata-ratanya adalah.....
a. 80,2
b. 80,8
c. 81,2
d. 81,6
Pembahasan :
7. Soal Statistika Kelas 12 : Rata-rata berat badan pada tabel frekuensi berikut adalah..... kg
 |
| Soal Statistika Kelas 12 gambar 4 |
a.62
b.62,2
c.62,5
d. 62,7
Pembahasan :
8. Soal Statistika Kelas 12 : Rata-rata tinggi badan siswa kelas XII ditulis dalam tabel frekuensi berikut.
 | |
| Soal Statistika Kelas 12 gambar 7 |
Rata-rata tinggi badan tersebut adalah... cm
a. 162 - 0,77
b. 162 + 0,63
c. 163 - 0,57
d. 163 + 0,21
Pembahasan :
Soal ini kita coba selesaikan dengan dua cara yaitu cara simpangan rata-rata sementara dan cara coding.
I. Cara simpangan rata-rata sementara
Pertama, kita tentukan rataan sementara yaitu nilai tengah di kelas ketiga. Kita dapatkan rataan sementara=163. Lalu kurangi nilai tengah tiap kelas dengan rataan sementara tersebut seperti tabel berikut
 | |
| Soal Statistika Kelas 12 gambar8 |
maka kita dapatkan rata-ratanya
=163 + (-20:35)
=163 - 0,57
II. Cara coding
Pertama, kita tentukan rataan sementara yaitu nilai tengah di kelas ketiga. Kita dapatkan rataan sementara=163. Lalu tentukan nilai coding tiap kelas dan kalikan dengan frekuensi sehingga didapat data seperti dalam tabel berikut
 | |
| Soal Statistika Kelas 12 gambar 9 |
Substitusi hasil yang didapat ke rumus coding
Rata-rata=163 - (-4:35).5
=163 - 0,57
9. Soal Statistika Kelas 12 : Median dari data nilai ulangan 95, 75, 75, 80, 90, 70, 90, 85, 80, 90 adalah...
a. 80
b. 82,5
c. 85
d. 87,5
Pembahasan :
Untuk mendapatkan median (nilai tengah) maka data harus kita urutkan dari yang terkecil hingga terbesar
70, 75, 75, 80, 80, 85, 90, 90, 90, 95
karena jumlah datum sepuluh, maka median berada pada ditengah datum ke 5 dan ke 6 yaitu 80 dan 85
Median=(80+85) : 2
=82,5
10. Soal Statistika Kelas 12 : Diketahui empat buah bilangan dengan nilai terkecil 32 dan nilai terbesar 58. Jika bilangan ke dua dan ke tiga mempunyai selisih 8 dan rata-rata keempat bilangan tersebut adalah 44,5, maka median dari keempat bilangan tersebut adalah....
a. 40
b. 44
c. 46
d. 48
Pembahasan :
Jika bilangan kedua kita misalkan a dan bilangan ketiga kita misalkan b, maka bilangan-bilangan itu adalah 32, a, b, 58
32+a+b+58=44,5 x 4
90+a+b =178
a+b =88
karena selisih a dan b=8, maka b=a+8
a+b =88
a+a+8=88
2a =88-8
a =80 : 4
=40
b=a + 8
=48
Median=(40+48) : 2
=44
11. Soal Statistika Kelas 12 : Median dari data pada tabel frekuensi di bawah adalah... cm
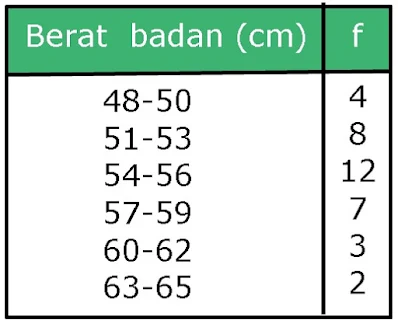 | |
|
a. 54,25
b. 54, 5
c. 54,75
d. 55
Pembahasan :
Kelas median di n : 2
n=Σf=4+8+12+7+3+2=36
36 : 2=18, maka ada di kelas ke tiga
Tentukan frekuensi kumulatif dengan menjumlahkan frekuensi kelas dengan jumlah frekuensi sebelumnya.
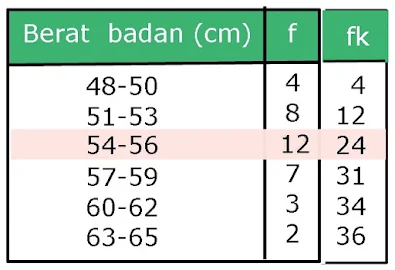 | |
|
Substitusi ke dalam rumus
12. Soal Statistika Kelas 12 : Modus dari pengamatan terhadap tinggi sebuah pohon yang disajikan pada tabel frekuensi berikut adalah...
 | ||
|
a. 81,4
b. 81,7
c. 82
d. 82,2
Pembahasan :
Frekuensi tertinggi adalah 16, maka kelas modus adalah pada kelas ke tiga.
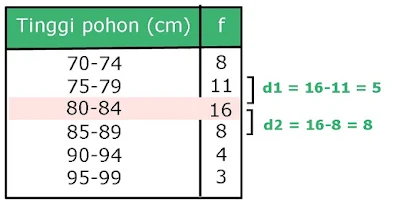 | |
|
Substitusi ke rumus modus
13. Soal Statistika Kelas 12 : Tentukan kuartil bawah dari data pada tabel frekuensi berikut
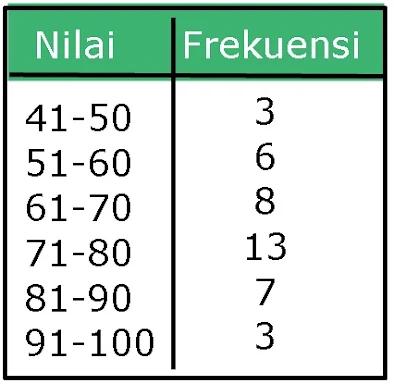 | ||
|
a. 61,5
b. 61,75
c. 62
d. 62,25
Pembahasan :
Kuartil bawah (Q1)=n/4
=(3+6+8+13+7+3)/4
=10 (ada di kelas ketiga)
Substitusi ke rumus kuartil bawah
a. 10 dan 2
b. 11 dan 3
c. 12 dan 2
d. 12 dan 3
Pembahasan :
Datum tengah atau datum ke empat=245 : 7=35
Maka data tersebut adalah 29, 31, 33, 35, 37, 39, 41
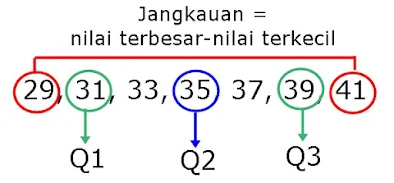 | |
|
=12
Simpangan kuartil=1/2 (Q3-Q1)
=1/2 (39-31)
=1/2(8)
= 4
15. Soal Statistika Kelas 12 : Simpangan rata-rata dari data 2, 5, 5, 7, 8, 3, 8, 9, 7 dan 6 adalah...
a. 1,5
b. 1,6
c. 1,8
d. 1,9
Pembahasan :
Rata-rata=(2+5+5+7+8+3+8+9+7+6) : 10
=6
16. Soal Statistika Kelas 12 : Perhatikan histogram di bawah
Simpangan rata-rata dari data pada histogram di atas adalah...
a. 3,75
b. 3,85
c. 3,95
d. 4,05
Pembahasan :
Pindahkan data dalam histogram ke tabel frekuensi. Tentukan rata-ratanya serta simpangan tiap kelasnya.
Rata-rata=1900 : 40
=47,5
Sustitusi ke rumus simpangan rata-rata untuk data kelompok
17. Ragam (varian) dari data no.16 adalah...
a. 27,25
b. 27,75
c. 25.5
d. 25,75
Pembahasan :
Kuadratkan nilai |xi-x| lalu kalikan dengan frekuensi kelas seperti berikut
18. Soal Statistika Kelas 12 : Ragam dari 20, 16, 14, 17, 13 adalah....
a. 5
b. 6
c. 6,5
d. 7
Pembahasan :
Rata-rata=20+16+14+17+13
5
=16
Ragam=(20-16)²+(16-16)²+(14-16)²+(17-16)²+(13-16)²
5
=16+0+4+1+9
5
=6
19. Soal Statistika Kelas 12 : Simpangan baku dari data 9, 7, 10, 8, 5, 6, 7, 8, 6 dan 9 adalah....
a. 1,25
b. 1.5
c. 2,25
d. 4,5
Pembahasan :
Rata -rata=9+7+10+8+5+6+7+8+6+9
10
=7,5
(9-7,5)² =2,25
(7-7,5)² =0,25
(10-7,5)²=6,25
(8-7,5)² =0,25
(5-7,5)² =6,25
(6-7,5)² =2,25
(7-7,5)² =0,25
(8-7,5)² =0,25
(6-7,5)² =2,25
(9-7,5)² =2,25 +
22,5
Ragam= 22,5
10
=2,25
Simpangan Baku=√R
=√225
=1,5
20. Soal Statistika Kelas 12 : Hamparan dari data histogram di bawah adalah...
a. 2,78
b. 3,05
c. 3,22
d. 3,25
Pembahasan :
Rumus Hamparan=Q3 - Q1, maka kita harus mencari nilai Q1 dan Q3
n=5+9+16+7+3=40
Q1=n/4 =10
Q3=3n/4=30
 | |
v
|
a. 3,75
b. 3,85
c. 3,95
d. 4,05
Pembahasan :
Pindahkan data dalam histogram ke tabel frekuensi. Tentukan rata-ratanya serta simpangan tiap kelasnya.
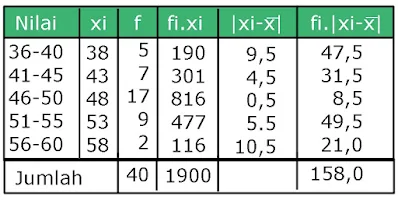 | |
|
Rata-rata=1900 : 40
=47,5
Sustitusi ke rumus simpangan rata-rata untuk data kelompok
17. Ragam (varian) dari data no.16 adalah...
a. 27,25
b. 27,75
c. 25.5
d. 25,75
Pembahasan :
Kuadratkan nilai |xi-x| lalu kalikan dengan frekuensi kelas seperti berikut
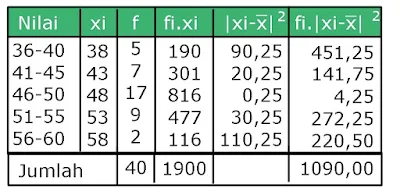 | ||
|
Jika sudah didapat nilainya, substitusi ke rumus ragam data kelompok
18. Soal Statistika Kelas 12 : Ragam dari 20, 16, 14, 17, 13 adalah....
a. 5
b. 6
c. 6,5
d. 7
Pembahasan :
Rata-rata=20+16+14+17+13
5
=16
Ragam=(20-16)²+(16-16)²+(14-16)²+(17-16)²+(13-16)²
5
=16+0+4+1+9
5
=6
19. Soal Statistika Kelas 12 : Simpangan baku dari data 9, 7, 10, 8, 5, 6, 7, 8, 6 dan 9 adalah....
a. 1,25
b. 1.5
c. 2,25
d. 4,5
Pembahasan :
Rata -rata=9+7+10+8+5+6+7+8+6+9
10
=7,5
(9-7,5)² =2,25
(7-7,5)² =0,25
(10-7,5)²=6,25
(8-7,5)² =0,25
(5-7,5)² =6,25
(6-7,5)² =2,25
(7-7,5)² =0,25
(8-7,5)² =0,25
(6-7,5)² =2,25
(9-7,5)² =2,25 +
22,5
Ragam= 22,5
10
=2,25
Simpangan Baku=√R
=√225
=1,5
20. Soal Statistika Kelas 12 : Hamparan dari data histogram di bawah adalah...
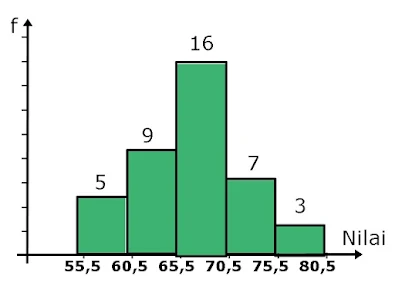 | |
|
a. 2,78
b. 3,05
c. 3,22
d. 3,25
Pembahasan :
Rumus Hamparan=Q3 - Q1, maka kita harus mencari nilai Q1 dan Q3
n=5+9+16+7+3=40
Q1=n/4 =10
Q3=3n/4=30
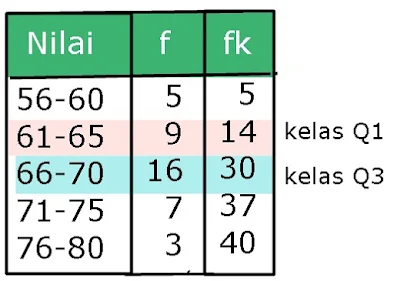 | |
|
Maka nilai Q1 dan Q3 adalah
mengenai kursus komputer
Hamparan=Q3 - Q1
=66,5 - 63,28
=3,22
Kamu bisa membaca uraian tentang menghitung rata-rata serta median dan kuartil di sini.
Menghitung rata-rata (mean)
Median dan kuartil
mengenai kursus komputer
Hamparan=Q3 - Q1
=66,5 - 63,28
=3,22
Kamu bisa membaca uraian tentang menghitung rata-rata serta median dan kuartil di sini.
Menghitung rata-rata (mean)
Median dan kuartil