Materi Soal Latihan Turunan Fungsi dari Bimbel Jakarta Timur ini meliputi fungsi aljabar, fungsi trigonometri, garis singgung dan garis normal, fungsi naik, fungsi turun serta aplikasi turunan. Pada postingan kali ini saya hanya akan memberikan soal-soal latihan yang dapat dicoba untuk latihan sebelum ulangan.
Dalam matematika, turunan fungsi dari variabel riil mengukur kepekaan terhadap perubahan nilai fungsi (nilai keluaran) terhadap perubahan argumennya (nilai masukan). Derivatif adalah alat dasar kalkulus. Misalnya, turunan dari posisi benda yang bergerak terhadap waktu adalah kecepatan benda: ini mengukur seberapa cepat posisi benda berubah ketika waktu berjalan.
Turunan dari fungsi variabel tunggal pada nilai input yang dipilih, jika ada, adalah kemiringan garis singgung ke grafik fungsi pada titik itu. Garis singgung adalah pendekatan linier terbaik dari fungsi di dekat nilai input itu. Untuk alasan ini, turunan sering digambarkan sebagai "laju perubahan sesaat", rasio perubahan sesaat dalam variabel dependen dengan variabel independen.
Turunan dapat digeneralisasikan ke fungsi beberapa variabel nyata. Dalam generalisasi ini, turunan diinterpretasikan ulang sebagai transformasi linier yang grafiknya (setelah translasi yang sesuai) merupakan aproksimasi linier terbaik terhadap grafik fungsi aslinya. Matriks Jacobian adalah matriks yang mewakili transformasi linier ini terhadap basis yang diberikan oleh pilihan variabel bebas dan terikat. Hal ini dapat dihitung dalam hal turunan parsial sehubungan dengan variabel independen. Untuk fungsi bernilai nyata dari beberapa variabel, matriks Jacobian direduksi menjadi vektor gradien.
Proses menemukan turunan disebut diferensiasi. Proses sebaliknya disebut antidiferensiasi. Teorema dasar kalkulus menghubungkan antidiferensiasi dengan integrasi. Diferensiasi dan integrasi merupakan dua operasi mendasar dalam kalkulus variabel tunggal.
turunan dari suatu fungsi f(x) menyatakan laju perubahannya dan dilambangkan dengan f'(x) atau df/dx.
Turunan Fungsi Aljabar
1) Turunan pertama dari f(x)=10x adalah…
a. 20
b. 10
c. 20x2
d. 10x2
Pembahasan :
Pembahasan :
f(x) =10x1
f’(x)=1.10.x0
=102) Jika f(x)=8, maka f’(x)=…
a. 0
b. 8
c. -8
d. 8x
Pembahasan :
F(x)=a
f'(x)=0
Pembahasan :
F(x)=a
f'(x)=0
3) Jika y=x4, maka y’=…
a. 4x
b. 4x3
c. x3
d. 4
Pembahasan :
y=x4
y’= 4.x4-1
Pembahasan :
y=x4
y’= 4.x4-1
y’= 4x3
4) Jika f(x)=-4x5, maka f’(x)=…
a. -4
b. -20x
c. -20x5
d. -20x4
Pembahasan :
f(x)=-4x5
f’(x)= -4. 5. x5-1
f’(x)= -20x4
5) y=4x3 - 3x2 +8x -5, dy/dx= …
a. 4x2-3x+8
b. 8x2-3x+8
c. 12x2-6x+8
d. 12x2-3x+8
Pembahasan :
y =4x3 - 3x2 + 8x -5
y'= 4.3x3-1 – 3.2x2-1 + 8.x1-1 + 0
=12x2–6x +8
6) Jika f(x) = 6x√x - 2/x², maka f'(x) =
a. 6x - 2/x
b. 6√x - 2/x
c. 9√x + 4/x
d. 9√x + 4/x³
Pembahasan :
a. 64
b. 32
c. 1/32
d. 1/64
Pembahasan :
f(x)= ⅓ x⁶
f'(x)=6 . ⅓ . x6-1
f'(x)=2x⁵
f'(2)=2(2)⁵
=64
Pembahasan :
f(x)= ⅓ x⁶
f'(x)=6 . ⅓ . x6-1
f'(x)=2x⁵
f'(2)=2(2)⁵
=64
8) Jika f(x)=3∛x2,maka f’(8)=…
a. 0
b. 1
c. 2
d. 4
Pembahasan :
f(x)=3.x2/3
f'(x)=(²/₃).3.x-1/3
f'(x)=2x-1/3
f’(8)=2(8)-1/3
=2(2)-1
=1
Pembahasan :
f(x)=3.x2/3
f'(x)=(²/₃).3.x-1/3
f'(x)=2x-1/3
f’(8)=2(8)-1/3
=2(2)-1
=1
9) Jika f(x)=6x√x, maka f’(4)=…
a. 4,5
b. 9
c. 13,5
d. 18
Pembahasan :
f(x)=6x3/2
f'(x)=³/₂ . 6 x1/2
f'(4)=9√4
=18
Pembahasan :
f(x)=6x3/2
f'(x)=³/₂ . 6 x1/2
f'(4)=9√4
=18
10) Turunan pertama dari fungsi y=(x2 + 2x + 3) (4x - 3) adalah…
a. 4x2 + 8x + 12
b. 8x2 + 12x + 3
c. 12x2 + 10x + 6
d. 12x2 + 2x + 6
Pembahasan :
Misalkan U= x2 + 2x + 3, maka U'=2x + 2
V= 4x - 3, maka V'=4

y'=(2x+2)(4x-3) + (x2 + 2x + 3) .4
y'=8x2 -6x+8x-6 + 4x2+8x+12
y'=12x2 + 10x + 6
Pembahasan :
Misalkan U= x2 + 2x + 3, maka U'=2x + 2
V= 4x - 3, maka V'=4

y'=(2x+2)(4x-3) + (x2 + 2x + 3) .4
y'=8x2 -6x+8x-6 + 4x2+8x+12
y'=12x2 + 10x + 6
11) Jka f(x)= (2x2+ 5x + 3)3, maka nilai dari f’(-2)=
a. - 9
b. 11
c. 21
d. 31
Pembahasan :
U= 2x2 + 5x + 3, maka U'=4x + 5
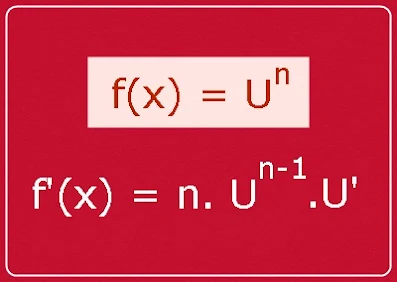
Pembahasan :
U= 2x2 + 5x + 3, maka U'=4x + 5
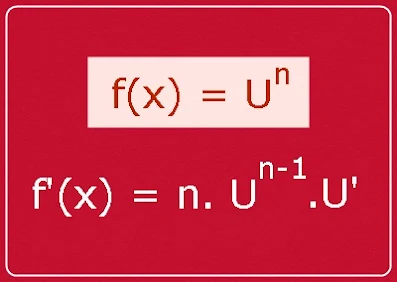
f’(x)= 3 (2x2 + 5x + 3)3-1. (4x+5)
= (12x+15)(2x2 + 5x + 3)2
f'(-2)=[12(-2)+15] [2(-2)2+5(-2)+3]2
=[-24+15][8-10+3]2
=(-9) (1)
=-9
12) Turunan kedua dari fungsi f(x)=3x4 + 2x3 −5x2 + 4x - 5 adalah…
a. 12x3+6x2-10x+4
b. 24x3+12x2-5x+4
c. 36x2 + 12x -10
d. 36x2 + 12x + 10
=-9
12) Turunan kedua dari fungsi f(x)=3x4 + 2x3 −5x2 + 4x - 5 adalah…
a. 12x3+6x2-10x+4
b. 24x3+12x2-5x+4
c. 36x2 + 12x -10
d. 36x2 + 12x + 10
Pembahasan :
f(x) =3x4 +2x3 − 5x2 + 4x – 5
f’(x)=12x3 + 6x2 – 10x + 4
f”(x)=36x2 + 12x - 10
13) Jika f(x)=(2x2 + 7x)3, maka f’(-1)=…
a. -45
b. - 9
c. 9
c. 9
d. 45
Pembahasan :
f(x)=(2x2 + 7x)3
f’(x)=3 (2x2 +7x)2 (4x+7)
f'(-2)= 3 (2(-1)2 +7(-1))2 (4(-1)+7)
=3 (2 - 7)2 (3)
=45
Pembahasan :
f(x)=(2x2 + 7x)3
f’(x)=3 (2x2 +7x)2 (4x+7)
f'(-2)= 3 (2(-1)2 +7(-1))2 (4(-1)+7)
=3 (2 - 7)2 (3)
=45
a. -9/2
b. 9/2
c. -2/9
d. 2/9
Pembahasan :
Misalkan U= x2 -3, U'=2x
V= 5–2x, V'=-2
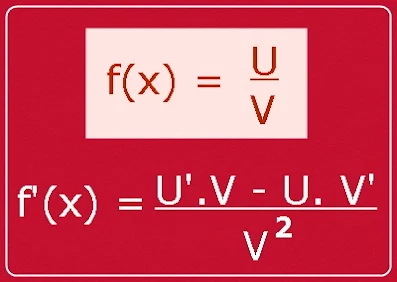

15) Turunanpertama dari fungsi f(x)=(2x2 + 3)5 (3x - 1)4 adalah….
a. 20 (2x2 + 3)4 . (3x-1)3
b. 80x (2x2 + 3)4 . (3x-1)3
c. (84x2 +20x+36) (2x2 + 3)4 . (3x-1)3
d. (84x2-20x+36) (2x2 + 3)4 . (3x-1)3
Pembahasan :
U=(2x2 + 3)5
U’=5(2x2+3)4.(4x)
=20x(2x2+3)4
V=(3x - 1)4
V’=4(3x-1)3.(3)
=12(3x-1)3
f’(x)=U’.V + U.V’
=20x(2x2+3)4. (3x- 1)4 + (2x2 +3)5 . 12(3x-1)3
=20x(3x-1) (2x2+3)4.(3x - 1)3 + 12(2x2 + 3) (2x2 + 3)4 . (3x-1)3
=[(60x2-20x)+(24x2+36)][(2x2 + 3)4.(3x-1)3]
= (84x2-20x+36) (2x2 +3)4 . (3x-1)3
16) Gradien garis singgung kurva y=x2+ 7x – 12 di titik berabsis -1 adalah…
21) Titik stasioner dari kurva y=x³ - 48x adalah ....
a. (-4,128) dan (4, -128)
b. (-4, -128) dan (4, 128)
c. (-4,96) dan (4,96)
d. (-4, -96) dan (4,96)
Pembahasan :
y'=0
3x² - 48 =0
3(x+4)(x-4)=0
x₁=-4 dan x₂=4
y₁=(-4)³ - 48(-4)
=-64 + 192
=128
y₂=(4)³ - 48(4)
=64 - 192
=- 128
Titik stasioner (-4,128) dan (4, -128)
22) Nilai maksimum fungsi f(x)=2x(x²-6) pada interval -2 ≤ x ≤ 2 adalah...
a. 1
b. 2
c. 3
d. 4
Pembahasan :
f(x)=2x³ - 6x
f'(x) =0
6x²-6=0
6(x+1)(x-1)=0
x=-1 dan x=1 (memenuhi interval)
f(-1)=2(-1)³ -6(-1)
=-2 + 6
=4
f(1)=2(1)³ -6(1)
=2 - 6
=-4
Nilai maksimum=4
23) Nilai maksimum dan minimum x³-3x²-24x + 4 pada interval -3 ≤ x ≤ 3 adalah...
a. 22 dan - 72
b. 22 dan -68
c. 32 dan -68
d. 32 dan - 76
Pembahasan :
3x²- 6x - 24=0
3(x²- 2x - 8)=0
(x+2) (x-4)=0
x₁=-2 dan x₂=4 (4 tidak memenuhi interval)
f(-3)=(-3)³ - 3(-3)² - 24(-3) + 4
=-27 -27 + 72 + 4
=22
f(-2)=(-2)³ - 3(-2)² - 24(-2) + 4
=-8 - 12 + 48 + 4
=32
f(3)=(3)³ - 3(3)² - 24(3) + 4 =27 - 27 - 72 + 4
=- 68
Maka nilai maksimum=32 dan minimum=- 68
24) Sebuah roket ditembakkan vertikal ke atas dan mencapai ketinggian h meter pada waktu t detik. Jika gerak roket tersebut memenuhi rumus h(t)=300t - 5t², maka ketinggian maksimum roket tersebut adalah...
a. 1.800 m
b. 3.600 m
c. 4.500 m
d. 6.000 m
Pembahasan :
titik maksimum tercapai ketika h'(t)=0
300 - 10t=0
- 10t=- 300
t=30 detik
h(30)=300(30) -5(30)²
=9000 - 4500
=4.500 m
25) Suatu proyek perbaikan jalan dikerjakan oleh x pekerja dengan gaji untuk setiap karyawan (3x - 90 + 800/x) ratus ribu rupiah. Agar biaya proyek minimum, maka jumlah karyawan yang dipekerjakan adalah....
a. 12 orang
b. 15 orang
c. 18 orang
d. 20 orang
Pembahasan :
Biaya total=(3x - 90 + 800/x).x
=3x² - 90 x + 800
Biaya minimum jika B'=0
6x - 90=0
6x =90
x =90:6
x =15 orang
a. 3
b. 5
c. 9
d. 12
Pembahasan :
m=y’
=2x + 7
dititik berabsis -1
m=2(-1) + 7
=5
17) Persamaan garis singgung kurva f(x)=(3x-2)2 yang sejajar dengan garis y + 3x=6 adalah…
a. y=3x + 1/4
b. y=3x + 7/4
c. y=-3x + 7/4
d. y=-3x – 7/4
Pembahasan :
garis y + 3x=6
m=-3
karenasejajar maka m1=m2
y’=m
2(3x-2).3=-3
18x– 12=-3
18x=-3 + 12
18x=9
x=9/18
x1=1/2
f(x)=(3x-2)2
y1 =(3(1/2)- 2)2
=1/4
y –1/4=-3(x – 1/2)
y =-3x + 3/2 + 1/4
y =-3x + 7/4
18) Fungsi f(x)=¹/₃ x³ + ³/₂ x² - 10x + 5 naik pada interval....
a. -5 < x < 2
b. x < -5 atau x > 2
c. -2 < x < 5
d. x < -2 atau x > 5
Pembahasan :
Fungsi naik jika f'(x) > 0
x² + 3x - 10 > 0
(x+5) (x-2) > 0
x=-5 dan x=2
x < -5 atau x > 2
19) Fungsi f(x)=x³ - 3x² - 45x turun pada interval ...
a. -5 < x < 3
b. x < -5 atau x > 3
c. -3 < x < 5
d. x < -3 atau x > 5
Pembahasan :
Fungsi turun jika f'(x) < 0
3x²-6x -45 < 0 (sederhanakan dengan dibagi 3)
x² - 2x -15 < 0
(x+3) (x-5) < 0
x=-3, x=5
-3 < x < 5
20) Nilai stasioner dari fungsi f(x)=-2x²+ 8x adalah...
a. -2
b. -1
c. 1
d. 2
Pembahasan :
Nilai stasioner dicapai ketika f'(x)=0
a. -2
b. -1
c. 1
d. 2
Pembahasan :
Nilai stasioner dicapai ketika f'(x)=0
-4x + 8=0
-4x =- 8
x =-8/-4
=2
-4x =- 8
x =-8/-4
=2
21) Titik stasioner dari kurva y=x³ - 48x adalah ....
a. (-4,128) dan (4, -128)
b. (-4, -128) dan (4, 128)
c. (-4,96) dan (4,96)
d. (-4, -96) dan (4,96)
Pembahasan :
y'=0
3x² - 48 =0
3(x+4)(x-4)=0
x₁=-4 dan x₂=4
y₁=(-4)³ - 48(-4)
=-64 + 192
=128
y₂=(4)³ - 48(4)
=64 - 192
=- 128
Titik stasioner (-4,128) dan (4, -128)
22) Nilai maksimum fungsi f(x)=2x(x²-6) pada interval -2 ≤ x ≤ 2 adalah...
a. 1
b. 2
c. 3
d. 4
Pembahasan :
f(x)=2x³ - 6x
f'(x) =0
6x²-6=0
6(x+1)(x-1)=0
x=-1 dan x=1 (memenuhi interval)
f(-1)=2(-1)³ -6(-1)
=-2 + 6
=4
f(1)=2(1)³ -6(1)
=2 - 6
=-4
Nilai maksimum=4
23) Nilai maksimum dan minimum x³-3x²-24x + 4 pada interval -3 ≤ x ≤ 3 adalah...
a. 22 dan - 72
b. 22 dan -68
c. 32 dan -68
d. 32 dan - 76
Pembahasan :
3x²- 6x - 24=0
3(x²- 2x - 8)=0
(x+2) (x-4)=0
x₁=-2 dan x₂=4 (4 tidak memenuhi interval)
f(-3)=(-3)³ - 3(-3)² - 24(-3) + 4
=-27 -27 + 72 + 4
=22
f(-2)=(-2)³ - 3(-2)² - 24(-2) + 4
=-8 - 12 + 48 + 4
=32
f(3)=(3)³ - 3(3)² - 24(3) + 4 =27 - 27 - 72 + 4
=- 68
Maka nilai maksimum=32 dan minimum=- 68
24) Sebuah roket ditembakkan vertikal ke atas dan mencapai ketinggian h meter pada waktu t detik. Jika gerak roket tersebut memenuhi rumus h(t)=300t - 5t², maka ketinggian maksimum roket tersebut adalah...
a. 1.800 m
b. 3.600 m
c. 4.500 m
d. 6.000 m
Pembahasan :
titik maksimum tercapai ketika h'(t)=0
300 - 10t=0
- 10t=- 300
t=30 detik
h(30)=300(30) -5(30)²
=9000 - 4500
=4.500 m
25) Suatu proyek perbaikan jalan dikerjakan oleh x pekerja dengan gaji untuk setiap karyawan (3x - 90 + 800/x) ratus ribu rupiah. Agar biaya proyek minimum, maka jumlah karyawan yang dipekerjakan adalah....
a. 12 orang
b. 15 orang
c. 18 orang
d. 20 orang
Pembahasan :
Biaya total=(3x - 90 + 800/x).x
=3x² - 90 x + 800
Biaya minimum jika B'=0
6x - 90=0
6x =90
x =90:6
x =15 orang
Semoga Bermanfaat






%20By%20Bimbel%20Jakarta%20Timur.webp)




