Soal Fungsi Kuadrat Kelas 9 By Bimbel Jakarta Timur

Bimbel Jakarta Timur sebelum lebih jauh akan menjelaskan apa itu Fungsi kuadrat, fungsi kuadrat adalah fungsi polinomial yang pada persamaannya memiliki variabel dengan pangkat tertingginya 2. Dalam materi fungsi ini kita pelajari ciri-ciri grafik fungsi kuadrat, sumbu simetri, nilai optimum (maksimum atau minimum) serta titik potongnya terhadap sumbu pada koordinat kartesius. 


Pada artikel ini kami berikan beberapa soal latihan tentang fungsi kuadrat beserta pembahasannya. Semoga yang kami uraikan dapat membuatmu lebih paham tentang materi ini. 

1. Jika suatu fungsi kuadrat f(x)=ax²+bx+c memiliki nilai a positif, maka kurva grafik fungsi tersebut....
a. tidak memotong sumbu y
b. tidak memotong sumbu x
c. terbuka ke atas
d. terbuka ke bawah

     Pembahasan :
     Nilai a menentukan bentuk kurva grafik fungsi kuadrat, yaitu 
     jika a > 0 maka kurva terbuka ke atas
     jika a < 0 maka kurva terbuka ke bawah

2. Nilai a, b dan c dari fungsi f(x)=-2x²+3(2x+5) adalah....
a. 2, 5 dan 8
b. -2, 3 dan 5
c. -2, 6 dan 5
d. -2, 6 dan 15

     Pembahasan : 
     f(x)=-2x²+3(2x+5)
           = -2x² + 6x + 15
     maka a=-2, b=6 dan c=15

3. Nilai f(-3) dari fungsi f(x)=x²-4x+2 adalah...
a. -1
b. 1
c. 5
d. 23

     Pembahasan : 
     f(x)   =x²-4x+2
     f(-3)=(-3)²-4(-3)+2
             =9 + 12 + 2
             =23

4. Jika y=x²jika digeser 3 satuan ke atas, maka rumus fungsinya menjadi…

a. y=x² – 3

b. y=x² + 3

c. y=(x - 3)²

d. y=(x + 3)²

     Pembahasan :
     Grafik fungsi akan bergeser ke atas jika nilai y bertambah 3
     y=x² + 3
     

5. Posisi grafik fungsi y=(x + 4)² terhadap grafik fungsi y=x² adalah...
a. 4 satuan di atas
b. 4 satuan di bawah
c. 4 satuan di kanan
d. 4 satuan di kiri

     Pembahasan : 
      Jika nilai x bertambah 4, maka grafik fungsi akan bergeser 4 satuan ke kiri 
     

6. Fungsi f(x)=x²- 5x + 6 memotong sumbu y di titik...
a. (0,-5)
b. (0,6)
c. (-5,0)
d. (6,0)

    Pembahasan : 
    Titik potong dengan sumbu ya di dapat jika x=0, maka
    f(0)=0²- 5(0) + 6
         =6
    x=0 dan y=6
    titik potong (0,6)

7. Fungsi kuadrat yang sumbu simetrinya sumbu y adalah...
a. y=x² - 9
b. y=x² + 7x + 12
c. y=x² -5x
d. y=(x - 4)²

     Pembahasan :
      Sumbu y berarti x=0
     karena persamaan sumbu simetri adalah x=-b/2a, maka b=0
     yang nilai b=0 adalah pilihan a. y=x² - 9
     

8. Fungsi kuadrat yang tidak memotong sumbu x adalah...
a. y= x² - 5x - 14
b. y= x² - 25
c. y= 2x² + 5x + 3
d. y= 3x² - 7x + 5

     Pembahasan :
     D > 0, memotong sumbu x di dua titik
     D=0, menyinggung sumbu x di satu titik
     D < 0, tidak memotong sumbu x

     a. y=x² - 5x - 14, nilai a=1, b=-5, c=-14
         D=b² - 4.a.c 
           =(-5)² - 4.1.-14 
           =81 (memotong di dua titik)
   
      b. y=x² - 25, nilai a=1, b=0, c=-25
          D=0² - 4.1.-25
             =100 (memotong di dua titik)

      c. y=2x² + 5x + 3, nilai a=2, b=5, c=3
          D=5² - 4.2.3
             =1 (memotong di dua titik

      d. y=3x² - 7x + 5, nilai a=3, b=-7, c=5
          D=-7² - 4.3.5
             =-11 (tidak memotong sumbu x)      

9. Fungsi f(x)=x² - 8x + 12 memotong sumbu x di titik ....
a. (-8,0) dan (12,0)
b. (8,0) dan (-12,0)
c. (2,0) dan (6,0)
d. (-2,0) dan (-6,0)

     Pembahasan : 
     memotong sumbu x, nilai fungsi=0
     x² - 8x + 12=0
     (x - 2) (x - 6)=0
     x - 2=0 dan x - 6=0
     x     =2 dan x     =6
     titik (2,0) dan (6,0)

10. Persamaan sumbu simetri fungsi y=3(x -5)² - 40 adalah...
a. x=-10
b. x=-5
c. x=5
d. x=10

     Pembahasan : 
     y=3(x -5)² - 40
       =3(x²-10x+25) - 40
       =3x² - 30x + 75 - 40

 
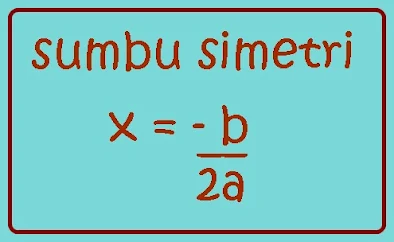
     x=-(-30)/2(3)
       =30/6
     x=5
     

11. Fungsi f(x)=2x²+ bx + 9 memiliki sumbu simetri x=3, maka nilai b=....
a. -12
b. -6
c. 6
d. 12

     Pembahasan : 
     sumbu simetri x=-b/2a
     3=-b/2(2)
     3=-b/4
     b=-12

12. Nilai minimum fungsi f(x)=x² - 6x - 16 adalah...
a. y=-25
b. y=-16
c. y=-9
d. y=-7

     Pembahasan : 

 
     
       y=(-6)² - 4.1.-16
               -4.1
       =36+64
           -4
       =-25

13. Fungsi f(x)=ax²+6x+8 mempunyai nilai minimum 5, maka nilai a²+a=....
a. 8
b. 9
c. 12
d. 16

     Pembahasan : 
     6² - 4.a.8 =5
        -4.a
     36 -32a   =5(-4a)
     36         =-20a + 32a
     36         =12a
     a=3

     a²+a=3² + 3
           =12

14. Grafik fungsi f(x)=x² + 7x – 18 akan ….

a. memotong sumbuy di dua titik

b. tidak memotongsumbu x

c. menyinggungsumbu x

d. memotong sumbux di dua titik

     Pembahasan :
     D=b² - 4.a.c
       =7² - 4.1.-18
       =49 + 72
       =121
     D > 0, memotong sumbu x di dua titik

15. Pernyataan berikut yang tidak sesuai dengan grafik fungsi f(x) =-4x² + 8x - 3 adalah...
a. memotong sumbu x di dua titik
b. persamaan sumbu simetri x=1
c. nilai minimum y=1
d. nilai maksimum y=1

     Pembahasan : 
     D=b² - 4.a.c
       =8² - 4.-4.-3
       =16 (memotong di dua titik) memenuhi
     sumbu simetri
      x=-b/2a
       =-8/2(-4)
       =1 memenuhi
     Nilai optimum
     y=b²-4ac
             -4a
       =    16   
          -4(-4)
       =1 
     nilai a < 0
     kurva terbuka ke bawah, maka nilai optimum adalah nilai maksimum
     c. nilai minimum y=1 tidak memenuhi

16. Pernyataan berikut yang sesuai dengan fungsi y=x²-5(2x-5) adalah...
a. memotong sumbu y di titik (0,-5)
b. memotong sumbu x di titik (2,0) dan (5,0)
c. menyinggung sumbu x di titik (5,0)
d. mempunyai nilai maksimum y=5

     Pembahasan : 
     y=x²-5(2x-5)
       = x² - 10x + 25
     Titik potong sumbu y, maka x=0
     y=0² - 10(0) + 25
     y=25, titik potong (0,25)
     Titik potong sumbu x, maka y=0
     x² - 10x + 25=0
     (x - 5) (x - 5)=0
      x=5, menyinggung sumbu x di (5,0)

17. Koordinat titik puncak grafik y=x²-4x-12 adalah...
a. (-2,-16)
b. (-2,16)
c. (2,-16)
d. (2,16)

     Pembahasan : 
     Titik puncak suatu fungsi kuadrat adalah titik yang dicapai ketika nilai x merupakan sumbu simetri dan nilai y merupakan nilai optimum.
     y=x²-4x-12 
     x=-b/2a
       =-(-4)/2.1
       =2
     y=b² - 4.a.c
            -4a
       =(-4)²- 4.1.(-12)
              -4.1
       =-16
     titik puncak (2,-16)

18. Tentukan persamaan fungsi yang mempunyi titik puncak (4,-1) dan melalui titik (1,8) !
a. y = x² - 8x + 17
b. y = x² - 8x + 16
c. y = x² - 8x + 15
d. y = x² + 8x +17

     Pembahasan : 
     Menentukan persamaan fungsi jika diketahui titik puncak dan satu titik lain yang dilalui adalah menggunakan rumus

      (xp,yp)=(4,-1), (x,y)=(1,8)
      substitusi ke dalam rumus untuk mendapatkan nilai a
      8 - (-1)=a (1 - 4)²
               9=9a
               a=1
      substitusi kembali nilai a dan titik puncak ke rumus
      y -(-1)=1 (x - 4)²
      y + 1   =x² - 8x + 16
      y         =x² - 8x + 15

19. Tentukan persamaan fungsi kuadrat yang grafiknya digambarkan seperti di bawah

a. y=-x² + 2x + 8

b. y=-x² - 2x + 8

c. y=x² - 2x - 8

d. y=x² - 2x + 8

     Pembahasan :

     Dari gambar kita ketahui bahwa kurva memotong sumbu x di dua titik.

     Jika diketahui dua titik potong sumbu x, kita gunakan rumus

     

     x₁=-2, x₂=4 dan (x,y)=(0,8)

     substitusi ke rumus untuk mendapatkan nilai a

     8=a (0 -(-2)) (0 - 4)

     8=a (2) (-4)

     8=-8a

     a=-1

     substitusi kembali nilai a dan titik potong sumbu x

     y=-1 (x-(-2))(x-4)

     y=-1(x+2)(x-4)

     y=-1(x²-2x-8)

     y=-x² + 2x + 8    

20. Tentukan persamaan fungsi yang melalui titik-titik (0,15), (1,6) dan (3,0)!
a. y=x² + 3x + 15
b. y=2x² + 11x + 5
c. y=-2x² - 11x + 15
d. y=2x² - 11x + 15


     Pembahasan :
     Substitusi tiap titik ke persamaan umum fungsi kuadrat
     y=ax² + bx + c

     (0,15) ➤ 15=a(0)² + b(0) + c
                  15=c
     (1,6)   ➤  6=a(1)² + b(1) + c
                   6=a + b + 15
            6 - 15=a + b    
                 -9=a + b   (I)
     (3,0)   ➤  0=a(3)² +b(3) + c
                   0=9a + 3b + 15
                -15=9a + 3b  (bagi 3 untuk menyederhanakan)
                 - 5=3a + b   (II)
     eliminasi (I) dan (II)
       a + b=-9
     3a + b=-5  -
     -2a     =-4
        a     =2
      a + b=-9
      2 + b=-9
           b=-9-2
           b=-11

     y=ax² + bx + c, maka
     y=2x² - 11x + 15

    

Semoga Bermanfaat

Artikel yang mungkin kamu perlu baca

Persamaan Kuadrat

Latihan Soal Persamaan Kuadrat

Mencari Akar-akar Persamaan Kuadrat

Grafik Fungsi Kuadrat

https://www.radarhot.com/2019/09/soal-fungsi-kuadrat-kelas-9.html