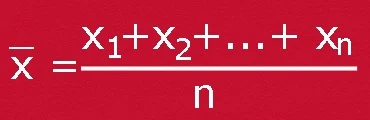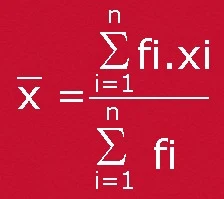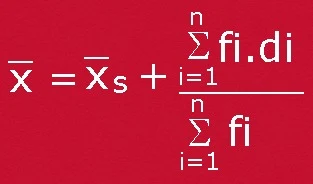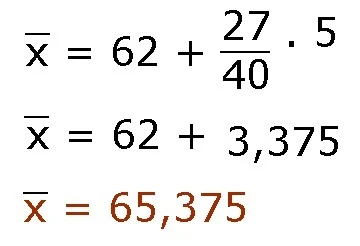Berikut adalah beberapa cara menghitung rata-rata dan soal yang berkenaan dengan rata-rata.
Rata-rata data tunggal
Data tunggal adalah data yang disusun sendiri dan belum dikelompokkan dalam kelas-kelas interval. Untuk menghitung rata-rata pada data tunggal maka semua data yang ada dijumlahkan lalu hasilnya dibagi banyaknya data.
contoh :
1. Tentukan rata-rata dari data nilai berikut : 8, 7, 8, 9, 10, 6, 7, 8, 9 ,10
Jawab :
2. Jika rata-rata dari data 59, a, 59, 58, 60, 63, 60 dan 59 adalah 60, maka tentukan nilai a!
Jawab :
Banyaknya data adalah 8 dan rata-rata adalah 60, maka
Jawab :
Banyaknya data adalah 8 dan rata-rata adalah 60, maka
3. Perhatikan tabel frekuensi di bawah !
Jika rata-rata dari data di atas adalah 164,75 maka tentukan nilai a !
Jawab :
Untuk mendapatkan jumlah seluruh nilai maka setiap datum dikalikan dengan frekuensinya. Banyaknya data adalah jumlah seluruh frekuensi.
Contoh :
1. Nilai rata-rata ulangan Matematika dari 32 orang adalah 7,5. Jika digabungkan dengan 8 orang lagi yang nilai rata-ratanya 8, maka nilai rata-rata sekarang menjadi.....
Jawab :
n₁=32, x₁=7,5, n₂=8, x₂=8
xgab . ngab =x₁.n₁+x₂.n₂
xgab . (32+8)=7,5.32+8.8
xgab . 40 =240 + 64
xgab =304 : 40
xgab =7,6
2. Rata-rata umur pegawai di suatu perusahaan adalah 36 tahun. Jika rata-rata umur pegawai pria adalah 40 dan rata-rata umur pegawai wanita adalah 30 tahun, maka perbandingan jumlah pegawai pria dan pegawai wanita adalah...
Jawab :
Misalkan jumlah pegawai pria= n₁, jumlah pegawai wanita= n₂
xgab =36, x₁=40, x₂= 30
xgab . ngab =x₁.n₁+x₂.n₂
36 . (n₁+n₂)=40n₁+30n₂
36n₁+ 36n₂ =40n₁+30n₂
36n₂ - 30n₂= 40n₁ - 36n₁
6 n₂ =4 n₁
6/4 = n₁/n₂
Perbandingan jumlah pegawai pria dan pegawai wanita
n₁/n₂ =6/4 =3/2 = 3 : 2
Contoh :
Tentukan rata-rata dari data kelompok di bawah
Jawab :
Untuk mendapatkan jumlah seluruh nilai maka setiap datum dikalikan dengan frekuensinya. Banyaknya data adalah jumlah seluruh frekuensi.
Rata-rata gabungan
Jika diketahui beberapa kelompok yang masing-masing mempunyai jumlah data dan rata-rata, maka ketika digabung akan dapat kita tentukan rata-rata gabungannya dengan rumus berikut :atau
xgab . ngab =x₁.n₁+x₂.n₂+...
Contoh :
1. Nilai rata-rata ulangan Matematika dari 32 orang adalah 7,5. Jika digabungkan dengan 8 orang lagi yang nilai rata-ratanya 8, maka nilai rata-rata sekarang menjadi.....
Jawab :
n₁=32, x₁=7,5, n₂=8, x₂=8
xgab . ngab =x₁.n₁+x₂.n₂
xgab . (32+8)=7,5.32+8.8
xgab . 40 =240 + 64
xgab =304 : 40
xgab =7,6
2. Rata-rata umur pegawai di suatu perusahaan adalah 36 tahun. Jika rata-rata umur pegawai pria adalah 40 dan rata-rata umur pegawai wanita adalah 30 tahun, maka perbandingan jumlah pegawai pria dan pegawai wanita adalah...
Jawab :
Misalkan jumlah pegawai pria= n₁, jumlah pegawai wanita= n₂
xgab =36, x₁=40, x₂= 30
xgab . ngab =x₁.n₁+x₂.n₂
36 . (n₁+n₂)=40n₁+30n₂
36n₁+ 36n₂ =40n₁+30n₂
36n₂ - 30n₂= 40n₁ - 36n₁
6 n₂ =4 n₁
6/4 = n₁/n₂
Perbandingan jumlah pegawai pria dan pegawai wanita
n₁/n₂ =6/4 =3/2 = 3 : 2
Rata-rata data kelompok
Data kelompok adalah data yang telah dikelompokkan dalam kelas-kelas yang memiliki interval. Hal pertama yang dilakukan untuk menghitung rata-rata data kelompok adalah menentukan nilai tengah tiap kelas (xi). Sehingga rata-rata dari data kelompok ditentukan dengan rumus berikutContoh :
Tentukan rata-rata dari data kelompok di bawah
Interval pada kelas pertama adalah 50-54, maka nilai tengahnya 52
Interval pada kelas kedua adalah 55-59, maka nilai tengahnya 57
Interval pada kelas ketiga adalah 60-64, maka nilai tengahnya 62
dan seterusnya
Interval pada kelas kedua adalah 55-59, maka nilai tengahnya 57
Interval pada kelas ketiga adalah 60-64, maka nilai tengahnya 62
dan seterusnya
Lalu kita hitung masing-masing nilai tengah kelas dengan frekuensi kelas. Setelah itu hitung jumlahnya seperti pada tabel berikut :
Jika data yang akan dihitung memiliki bilangan berjumlah banyak, seringkali membuat kita malas menghitungnya atau mungkin juga tidak teliti. Ada cara untuk lebih menyederhanakan penghitungan rata-rata, yaitu dengan menggunakan simpangan rata-rata sementara dan cara coding.
Kita tentukan rata-rata sementara dari nilai tengah kelas yang berada di tengah. Lalu hitung simpangan rata-rata sementara masing-masing kelas yaitu di, dimana di=xs - xi
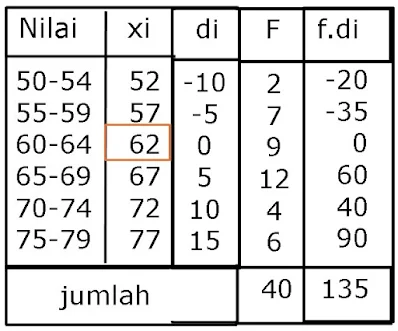
Sekarang kita coba contoh soal sebelumnya tetapi menggunakan cara ini. Kita ambil rata-rata sementara yaitu 62.
Simpangan rata-tara sementara kelas pertama=52-62=-10
Simpangan rata-tara sementara kelas kedua =57-62=-5
Simpangan rata-tara sementara kelas ketiga =62-62=0
Simpangan rata-tara sementara kelas keempat=67-62=5
dan seterusnya
Penyajian data selain dengan menulis nilainya satu persatu, bisa juga dengan mendaftarnya pada tabel frekuensi juga bisa berupa diagram contohnya diagram batang atau histogram. Sebenarnya perhitungan rata-ratanya sama saja, hanya kita harus bisa menganalisa data pada histogram. Untuk lebih mudah, bisa terlebih dahulu kita transformasi data pada histogram ke tabel frekuensi.
Contoh :
1. Tentukan rata-rata nilai ulangan berikut
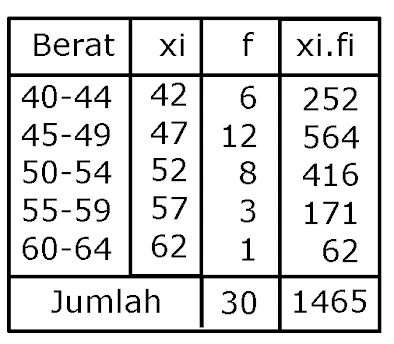
2. Tentukan rata-rata berat badan berikut
maka rata-ratanya=2615 : 40
=65,375
Jika data yang akan dihitung memiliki bilangan berjumlah banyak, seringkali membuat kita malas menghitungnya atau mungkin juga tidak teliti. Ada cara untuk lebih menyederhanakan penghitungan rata-rata, yaitu dengan menggunakan simpangan rata-rata sementara dan cara coding.
Menggunakan simpangan rata-rata sementara
Kita tentukan rata-rata sementara dari nilai tengah kelas yang berada di tengah. Lalu hitung simpangan rata-rata sementara masing-masing kelas yaitu di, dimana di=xs - xi
Sekarang kita coba contoh soal sebelumnya tetapi menggunakan cara ini. Kita ambil rata-rata sementara yaitu 62.
Simpangan rata-tara sementara kelas pertama=52-62=-10
Simpangan rata-tara sementara kelas kedua =57-62=-5
Simpangan rata-tara sementara kelas ketiga =62-62=0
Simpangan rata-tara sementara kelas keempat=67-62=5
dan seterusnya
Dari hasil di atas, kita substitusi ke rumus
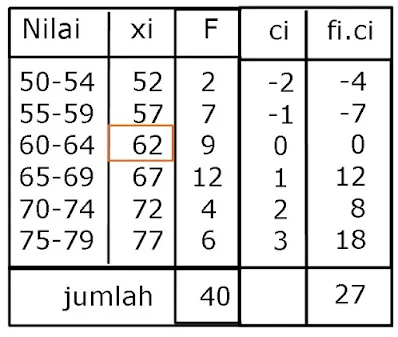
Menggunakan cara coding
Cara ini tetap menggunakan nilai tengah tiap kelas juga rata-rata sementara. Pada cara coding, nilai ci pada kelas rata-rata sementara adalah 0. Kode untuk kelas sebelumnya adalah -1, -2,-3 dan seterusnya, sedangkan kode untuk kelas setelahnya adalah 1,2,3 dan seterusnya.
Rumus rata-rata dengan cara coding atau kode adalah
Sekarang kita coba dari soal sebelumnya untuk kita selesaikan menggunakan cara coding.
Besarnya interval kita dapatkan dengan mengurangi tepi selisih tepi kelas.
i=55-50=5
Rata-rata data bentuk histogram
Penyajian data selain dengan menulis nilainya satu persatu, bisa juga dengan mendaftarnya pada tabel frekuensi juga bisa berupa diagram contohnya diagram batang atau histogram. Sebenarnya perhitungan rata-ratanya sama saja, hanya kita harus bisa menganalisa data pada histogram. Untuk lebih mudah, bisa terlebih dahulu kita transformasi data pada histogram ke tabel frekuensi.
Contoh :
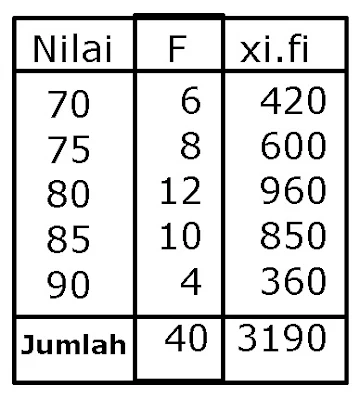
1. Tentukan rata-rata nilai ulangan berikut
Data pada histogram disajikan dalam tabel frekuensi data tunggal berikut
Maka didapatkan rata-rata nilai ulangan adalah 3.190 : 40=79,75
Kelas I
tepi bawah=39,5 ; tepi atas=44,5 ; interval kelas=40-44
Kelas II
tepi bawah=44,5 ; tepi atas=49,5 ; interval kelas=45-49
Kelas III
tepi bawah=49,5 ; tepi atas=54,5 ; interval kelas=50-54
Kelas IV
tepi bawah=54,5 ; tepi atas=59,5 ; interval kelas=55-59
Kelas V
tepi bawah=59,5 ; tepi atas=64,5 ; interval kelas=60-64
Tabel frekuensinya
Maka didapatkan rata-rata berat badan 1.465 : 30=48,83 kg