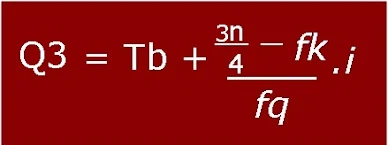Median atau nilai tengah adalah salah satu ukuran pemusatan data. Median merupakan nilai di tengah sekumpulan data yang nilainya berurutan.
Median Data Tunggal
Langkah pertama dalam menentukan median data tunggal adalah mengurutkan angka-angka yang ada dari yang nilainya terkecil hingga terbesar.Langkah kedua adalah menemukan angka yang letaknya di tengah. Jika jumlah angka pada data adalah ganjil, maka angka yg di tengah adalah median. Jika angka pada data jumlahnya genap, maka ada dua angka yang berada di tengah. Nilai mediannya adalah jumlah kedua data dibagi 2.
Contoh :
1. Median dari data 7, 6, 9, 8, 9 adalah....
2. Median dari data 17, 11, 15, 16, 12, 18, 15, 19, 13, 17 adalah...
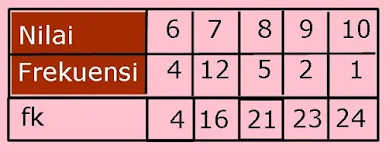
3. Tentukan median dari data pada tabel frekuensi berikut
Pertama kita tentukan frekuensi kumulatif tiap kelas
Frekuensi kumulatif=24
Median berada di datum (24+1) : 2=12,5 (datum 12 dan 13)
Median=7
Median Data Kelompok
1. Hal penting dalam menentukan median data kelompok adalah menentukan frekuensi kumulatif.
2. Setelah itu tentukan kelas median yaitu letak datum yang ditengah atau n/2.
3. Tentukan nilai-nilai yang akan kita substitusi ke dalam rumus median berikut:
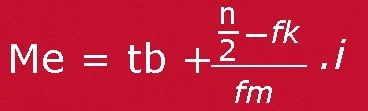 |
| Rumus Median |
tb=tepi bawah
n=jumlah data
fk=frekuensi kumulatif di atas kelas median
fm=frekuensi kelas median
i=interval kelas
Contoh :
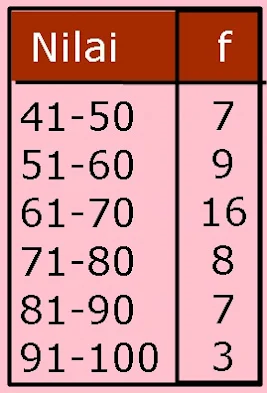
1. Tentukan median data berikut
Tentukan frekuensi kumulatif tiap kelas
Kelas median adalah letak datum ke n/2=50/2=25 yaitu kelas ke 3
Tb=60,5
fk =16
fm=16
i =10
maka
Me=60,5 + 25 - 16 . 10
16
=60,5 + 5,625
=66,125
Kuartil adalah bilangan yang membagi data yang sudah berurutan dari yang terkecil sampai terbesar menjadi empat bagian. Ada tiga jenis kuartil, yaitu kuartil bawah atau kuartil pertama (Q1), kuartil tengah atau kuartil kedua (Q2) dan kuartil atas atau kuartil ketiga (Q3). Kuartil tengah juga merupakan median. Untuk lebih jelasnya perhatikan gambar berikut
Kuartil Data Tunggal
Langkah pertama untuk menentukan kuartil juga dengan mengurutkan angka-angka pada data dari yang terkecil sampai terbesar.
Kuartil bawah adalah 1/4 dari data=1/4 (n+1)
Kuartil tengah adalah 1/2 dari data=1/2 (n+1)
Kuartil atas adalah 3/4 dari data=3/4 (n+1)
Contoh :
1. Diketahui data 80, 72, 75, 73, 77, 79, 74. Tentukan kuartil bawah, kuartil tengah dan kuartil atasnya !
Urutan data : 72, 73, 74, 75, 77, 79, 80
Cara mengelompokkan data
Tetapkan yang posisi di tengah sebagai Q2. Terbentuk dua kelompok yang dipisahkan oleh Q2. Posisi tengah dari kelompok pertama adalah Q1, dan posisi tengah dari kelompok kedua adalah Q3.
Maka Q1=73
Q2=75, dan
Q3=79
Cara posisi datum
n=7
Q1=datum ke 1/4 (n+1)
=1/4 (7+1)
=datum ke-2
=73
Q2=datum ke 1/2 (7+1)
=datum ke-4
=75
Q3=datum ke 3/4 (7+1)
=datum ke-6
=79
Kuartil Data Kelompok
Seperti telah disebutkan sebelumnya bahwa kuartil tengah atau Q2 juga merupakan median. Rumus untuk mencari Q2 adalah sama juga dengan rumus median. Ini berlaku pada data tunggal maupun data kelompok. Lalu bagaimana dengan rumus untuk mencari kuartil bawah (Q1) dan kuartil atas (Q3)? Pada prinsipnya kita menggunakan rumus yang sama, hanya saja angka yang berbeda.
 |
| Rumus Kuartil Bawah |
Rumus Kuartil Atas
tb=tepi bawah
n=jumlah data
fk=frekuensi kumulatif di atas kelas kuartil
fq=frekuensi kelas kuartil
i=interval kelas
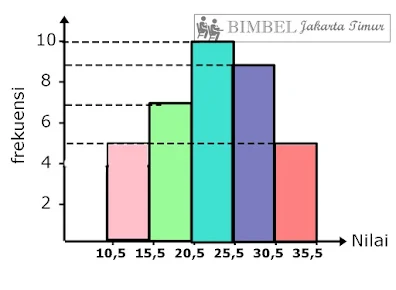
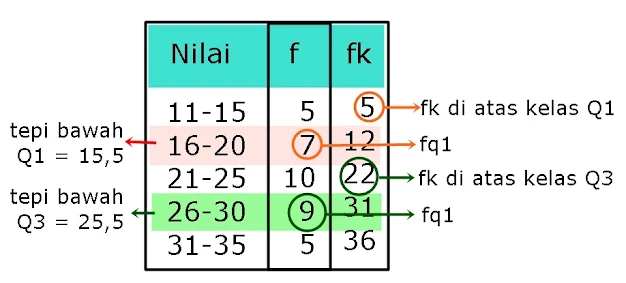
Mari berlatih dengan menentukan kuartil bawah dan kuartil atas pada data histogram berikut
Jika data tersebut kita buat dalam bentuk tabel frekuensi maka di dapat seperti berikut
Interval=5
Frekuensi total (n)=36
Q1=1/4 (36)=9
ada di kelas ke-2 dengan tepi bawah 15,5
Q3=3/4 (36)=27
ada di kelas ke-4 dengan tepi bawah 25,5
Substitusi ke rumus
Q1=15,5 + 9 - 5 . 5
7
=15,5 + 2,857
=18,357
Q3=25,5 + 27-22 . 5
9
=25,5 + 2,778
=28,278
Hamparan atau jangkauan antar kuartil adalah nilai selisih dari kuartil atas (Q3) dengan kuartil bawah (Q1).
H=Q₃ - Q₁
Simpangan Kuartil atau jangkauan semi interkuartil adalah nilai setengah dari selisih dari kuartil atas (Q3) dengan kuartil bawah (Q1). Maka nilai Simpangan Kuartil adalah setengah dari hamparan.
Qd=½ (Q₃ - Q₁)
Contoh :
1. Tentukan hamparan dan simpangan kuartil dari 30, 55, 40, 45, 35, 50, 40, 35, 45, 45
Jawab :
Urutan data dari yang terkecil 30, 35, 35, 40, 40, 45, 45, 45, 50, 55
H=Q3 - Q1
=45 - 35
=10
Qd=½ (Q3 - Q1)
=½ (10)
=5
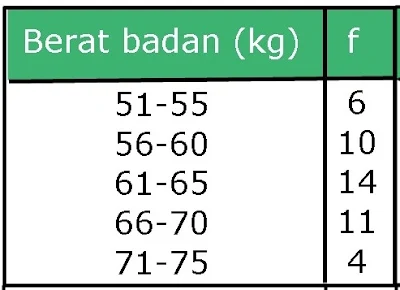
2. Tentukan hamparan dan simpangan kuartil dari tabel frekuensi berikut
Tentukan frekuensi kumulatif lalu kelas Q1 dan Q3
n=48
Q1=¼ (48)=12 ( kelas ke dua)
Q1=55,5 + 12 - 6 . 5
10
=55,5 + 3
=58,5
Q3=¾ (48)=36 (kelas ke 4)
Q3=65,5 + 36 - 30 . 5
11
=65,5 + 2,727
=68, 227
Maka H=Q3 - Q1
=68,227 - 58,5
=9,272
Qd=½ (Q3 - Q1)
=½ (9,272)
=4,636