Materi Relasi Dan Fungsi dipelajari di kelas 8 semester 1. Dengan mempelajari materi ini, diharapkan mengerti cara mengamati, mengolah data dan mengkomunikasikan data yang diberikan.Relasi adalah hubungan yang memasangkan antara anggota suatu himpunan dengan anggota himpunan lainnya. Relasi antara dua himpunan bisa dinyatakan dengan tiga cara, yaitu : diagram panah, himpunan pasangan berurutan dan diagram cartesius.

1. Diagram panah
Diagram panah adalah diagram yang menggambarkan dua himpunan yaitu himpunan daerah asal dan daerah kawan lalu dihubungkan dengan garis berpanah yang menunjukkan relasinya.contoh :
a. Empat orang anak yaitu Ali, Burhan, Candra dan Damai ditanyakan tentang jenis olahraga yang disukai. Ali menyukai futsal dan karate, Burhan hanya menyukai basket, Candra menyukai futsal dan basket, sedangkan Damai menyukai karate. Diagram panah dengan relasi menyukai digambarkan sebagai berikut:
Maka relasi diagram panah di atas adalah anggota himpunan A menyukai anggota himpunan B
b. Perhatikan diagram di bawah dan tentukan relasinya
Dari diagram panah di atas kita bisa melihat bahwa
2 dipasangkan dengan 8 dan 103 dipasangkan dengan 9
4 dipasangkan dengan 8
5 dipasangkan dengan 10
Bisa kita simpulkan relasi tersebut adalah relasi "faktor dari" karena anggota himpunan A adalah faktor dari anggota himpunan B yang dipasangkannya.
2. Himpunan pasangan berurutan
Himpunan pasangan berurutan adalah himpunan yang berisi daftar pasangan dari suatu realsi yang dituliskan dalam bentuk (x,y) dimana x adalah anggota daerah asal dan y adalah anggota daerah hasil.contoh
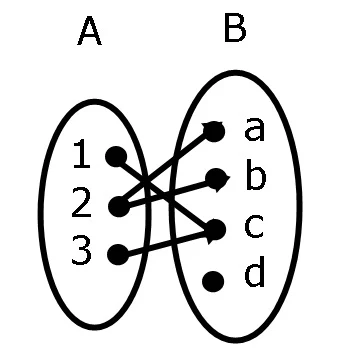
Perhatikan diagram panah berikut!
Himpunan pasangan berurutannya adalah :
{(1,c), (2,a), (2,b), (3,c)}
3. Diagram cartesius
Diagram cartesius adalah sistem kordinat yang digunakan untuk meletakkan titik pada penggambaran objek berdasarkan pemasukan nilai sumbu x dan nilai sumbu y dimana titik pertemuan ini nilai sumbu x dan sumbu y titik kordinat dibentuk.contoh :
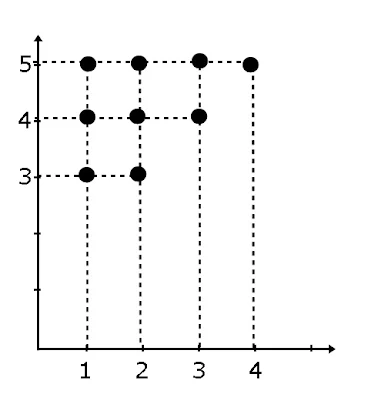
Diagram cartesius dari relasi "kurang dari" himpunan A{1, 2, 3, 4}ke himpunan B{3, 4, 5}
Fungsi (pemetaan) adalah relasi khusus dari himpunan A dan himpunan B yang memasangkan setiap anggota A dengan tepat satu anggota B. Ingat ya, tepat satu artinya tidak boleh kurang ataupun lebih.
Dari definisi di atas bisa kita simpulkan bahwa pada fungsi himpunan A ke himpunan B harus memenuhi syarat :
1. setiap anggota himpunan A atau daerah asal harus memiliki pasangan
2. setiap anggota A hanya mempunyai satu pasangan ke anggota B
contoh bukan pemetaan
a.
karena ada anggota A yang tidak memiliki pasangan
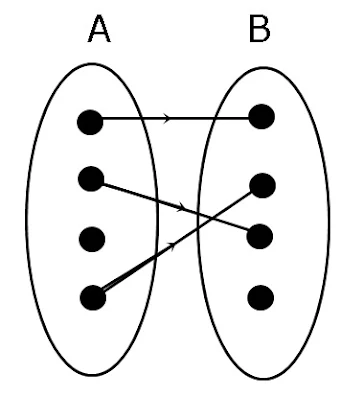
b.
karena ada anggota A yang memiliki lebih dari satu pasangan
Daerah kawan (kodomain) adalah semua anggota himpunan B pada pemetaan himpunan A ke himpunan B
Daerah hasil (range) adalah anggota himpunan B yang merupakan pasangan dari anggota himpunan A pada pemetaan himpunan A ke himpunan B
contoh :
Istilah-istilah dalam pemetaan
Daerah asal (domain) adalah semua anggota himpunan A pada pemetaan himpunan A ke himpunan BDaerah kawan (kodomain) adalah semua anggota himpunan B pada pemetaan himpunan A ke himpunan B
Daerah hasil (range) adalah anggota himpunan B yang merupakan pasangan dari anggota himpunan A pada pemetaan himpunan A ke himpunan B
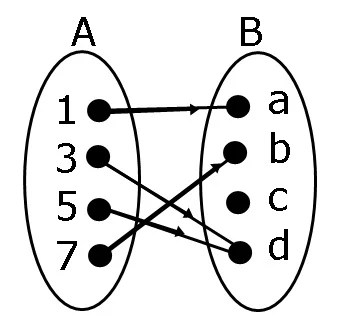
contoh :
Daerah asal={1,3,5,7}
Daerah kawan={a,b,c,d}
Daerah hasil={a,b,d}
Banyaknya pemetaan
Jika banyaknya anggota himpunan A adalah n(A)=a dan banyaknya anggota himpunan B adalah n(B)=b, maka :
⇒ Banyaknya pemetaan yang mungkin dari himpunan A ke himpunan B adalah ba
Contoh
Tentukan banyaknya pemetaan dari himpunan A={1, 4, 9}ke himpunan B={a, b}!
Jawab:
A={1, 4, 9}, n(A)=3
B={a, b}, n(B)=2
Banyaknya pemetaan yang mungkin dari himpunan A ke himpunan B adalah ba
= 23 =8
contoh :
Pada suatu pemetaan f :x → 2x + 1 dengan daerah asal{0, 1, 2, 3}, tentukan :
a. bayangan dari 2 pada fungsi f
b. daerah hasil
jawab:
a. rumus fungsi f(x)=2x + 1
bayangan 2
f(2)=2(2) + 1
=4 + 1
=5
b. Daerah asal{0, 1, 2, 3}
f(0)=2(0) + 1=1
f(1)=2(1) + 1=3
f(2)=2(2) + 1=5
f(3)=2(3) + 1=7
Maka daerah hasil={1, 3, 5, 7}
2) Tentukan daerah hasil dengan mensubstitusi anggota daerah asal ke rumus fungsi
3) Tentukan pasangan berurutan dari fungsi
4) Gambar sumbu datar x dan sumbu tegak y
5) Tentukan letak pasangan berurutan (x,y) pada bidang tersebut lalu beri noktah (titik)
6) Buat kurva yang menghubungkan semua noktah yang telah digambar
contoh :
Buatlah grafik fungsi dengan daerah asal{0, 1, 2, 3, 4}yang rumus fungsinya f(x)=3x - 2
Jawab :
{0, 1, 2, 3, 4, 5}
f(x)=3x - 2
f(0)=3(0) - 2=-2
f(1)=3(1) - 2=1
f(2)=3(2) - 2=4
f(3)=3(3) - 2=7
f(4)=3(4) - 2=10
Pasangan berurutan{(0,-2), (1,1), (2,4), (3,7), (4,10)}
Daerah kawan={a,b,c,d}
Daerah hasil={a,b,d}
Banyaknya pemetaan
Jika banyaknya anggota himpunan A adalah n(A)=a dan banyaknya anggota himpunan B adalah n(B)=b, maka :
⇒ Banyaknya pemetaan yang mungkin dari himpunan A ke himpunan B adalah ba
Contoh
Tentukan banyaknya pemetaan dari himpunan A={1, 4, 9}ke himpunan B={a, b}!
Jawab:
A={1, 4, 9}, n(A)=3
B={a, b}, n(B)=2
Banyaknya pemetaan yang mungkin dari himpunan A ke himpunan B adalah ba
= 23 =8
Menghitung nilai fungsi
Jika anggota daerah asal dipetakan pada suatu aturan fungsi f : x → ax + b, maka rumus fungsinya adalah f(x)=ax + b dan nilai fungsi ditentukan dengan mensubstitusi anggota daerah asal pada nilai x dalam rumus fungsi tersebut.contoh :
Pada suatu pemetaan f :x → 2x + 1 dengan daerah asal{0, 1, 2, 3}, tentukan :
a. bayangan dari 2 pada fungsi f
b. daerah hasil
jawab:
a. rumus fungsi f(x)=2x + 1
bayangan 2
f(2)=2(2) + 1
=4 + 1
=5
b. Daerah asal{0, 1, 2, 3}
f(0)=2(0) + 1=1
f(1)=2(1) + 1=3
f(2)=2(2) + 1=5
f(3)=2(3) + 1=7
Maka daerah hasil={1, 3, 5, 7}
Membuat grafik fungsi
1) Tentukan daerah asal2) Tentukan daerah hasil dengan mensubstitusi anggota daerah asal ke rumus fungsi
3) Tentukan pasangan berurutan dari fungsi
4) Gambar sumbu datar x dan sumbu tegak y
5) Tentukan letak pasangan berurutan (x,y) pada bidang tersebut lalu beri noktah (titik)
6) Buat kurva yang menghubungkan semua noktah yang telah digambar
contoh :
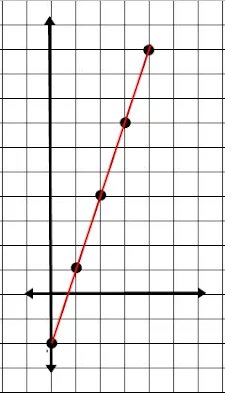
Buatlah grafik fungsi dengan daerah asal{0, 1, 2, 3, 4}yang rumus fungsinya f(x)=3x - 2
Jawab :
{0, 1, 2, 3, 4, 5}
f(x)=3x - 2
f(0)=3(0) - 2=-2
f(1)=3(1) - 2=1
f(2)=3(2) - 2=4
f(3)=3(3) - 2=7
f(4)=3(4) - 2=10
Pasangan berurutan{(0,-2), (1,1), (2,4), (3,7), (4,10)}
Korespondensi satu-satu adalah relasi di mana setiap anggota di A dipasangkan dengan satu anggota di B dan setiap anggota di B dipasangkan dengan satu anggota di A. Maka jumlah anggota himpunan A sama dengan jumlah anggota himpunan B atau n(A)=n(B)
Contoh korespondensi satu-satu antara lain siswa dengan tempat duduknya, negara dengan lagu kebangsaannya dan lain-lain.
n!=n x (n-1) x (n-2)... x 2 x 1
contoh :
Berapa banyak korespondensi satu-satu dari himpunan A={huruf vokal}dan himpunan B={jari tangan kanan}?
Jawab :
n(huruf vokal)=n(jari tangan)=5
banyaknya korespondensi satu-satu yang mungkin adalah
5!=5 x 4 x 3 x 2 x 1=120
Demikian materi Relasi Dan Fungsi yang dapat kami sajikan. Semoga membantumu untuk lebih memahaminya.
Contoh korespondensi satu-satu antara lain siswa dengan tempat duduknya, negara dengan lagu kebangsaannya dan lain-lain.
Banyaknya korespondensi satu-satu
Jika n(A)=n(B)=n, maka banyaknya semua korespondensi satu-satu yang mungkin adalah n ! (n faktorial)n!=n x (n-1) x (n-2)... x 2 x 1
contoh :
Berapa banyak korespondensi satu-satu dari himpunan A={huruf vokal}dan himpunan B={jari tangan kanan}?
Jawab :
n(huruf vokal)=n(jari tangan)=5
banyaknya korespondensi satu-satu yang mungkin adalah
5!=5 x 4 x 3 x 2 x 1=120
Demikian materi Relasi Dan Fungsi yang dapat kami sajikan. Semoga membantumu untuk lebih memahaminya.