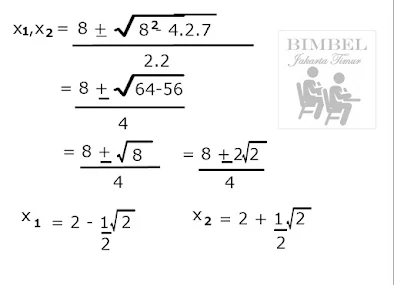Persamaan kuadrat adalah persamaan yang variabelnya memiliki pangkat tertinggi sama dengan dua. Secara umum bentuk persamaan kuadrat adalah
Contoh - contoh persamaan kuadrat
2x² + 5x + 4=0
3x² - 12x =0
x² + 8 =0
x² - 4x + 3 =0
2x² =0
Akar-akar persamaan kuadrat adalah nilai penyelesaian yang memenuhi suatu persamaan kuadrat sehingga persamaan itu bernilai nol. Ada tiga cara untuk mencari akar- akar persamaan kuadrat, yaitu dengan cara faktorisasi, melengkapkan kuadrat sempurna dan rumus abc.
1. Faktorisasi
Cara faktorisasi digunakan pada persamaan kuadrat yang memiliki akar-akar bilangan rasional. Sebelum melakukan faktorisasi, kita perhatikan terlebih dahulu bentuk persamaan kuadratnya. Berapa suku yang ada dalam persamaan tersebut serta nilai koefisien dari suku x².
- Persamaan kuadrat dengan dua suku
a. 3x² - 6 =0 nilai b=0, a dan c dapat dibagi angka yang sama
3 (x²- 2)=0
x²-2=0
x² =2
x =土 √2
b. 2x² - 6x =0 nilai c=0, a dan b dapat dibagi angka yang sama
2x (x - 3)=0
2x=0 dan x - 3=0
x =0 dan x =3
c. 4x² - 81=0 nilai b=0, a dan c dapat diakar
(2x + 9) (2x - 9)=0 2x adalah akar dari 4x² dan 9 adalah akar dari 81
2x + 9=0 dan 2x - 9=0
2x =-9 dan 2x =9
x =-⁹/₂ dan x = ⁹/₂
- Persamaan kuadrat dengan tiga suku
a. Jika a=1
x² + (p+q) x + (p.q)=0
(x+p)=0 dan (x+q)=0
contoh : x² + 7x + 12=0
7=3 + 4 dan 12=3x4
(x+3) (x+4)=0
x+3=0 dan x+4=0
x =-3 dan x =-4
b. Jika a > 1
ax² + bx + c=0 dengan axc=pxq dan b=p+q
a (x+p/a) (x+q/a)=0
contoh : 3x² + 4x - 4=0
x+2=0 dan x-2/3=0
x =-2 dan x =2/3
2. Melengkapkan kuadrat sempurna
Prinsip umumnya adalah
Contoh :
a. x² - 8x + 12 =0
Langkah 1. Pindahkan c ke ruas kanan
x² - 8x = -12
Langkah 2. Tambahkan kedua ruas dengan (b/2)²
x² - 8x + (-4)²= -12 + (-4)²
Langkah 3. Ubah ruas kiri ke bentuk (x+p)²
(x-4)² =4
Langkah 4. Kedua ruas diakar
√(x-4)² = √4
(x-4) =土 2
x-4=-2 dan x-2=2
x=-2+4 dan x=2+2
x =2 dan x =4
b. 3x² - 10x + 8 =0 jika a > 1, maka bagi dulu dengan a
(3x² - 10x + 8=0) : 3
x² - ¹⁰/₃x + ⁸/₃ =0 langkah selanjutnya sama seperti contoh a
x² - ¹⁰/₃x =-⁸/₃
x² - ¹⁰/₃x + (-⁵/₃)² =- ⁸/₃ + (-⁵/₃)²
(x - ⁵/₃)² =¹/₉
x - ⁵/₃ =±¹/₃
x=- ¹/₃ + ⁵/₃ dan x= ¹/₃ + ⁵/₃
x=⁴/₃ dan x=2
3. Rumus abc
Berdasarkan rumus umum persamaan kuadrat kita dapatkan nilai a dan b sebagai koefisien suku x² dan x, serta c sebagai konstanta. Rumus abc untuk menentukan akar-akar persamaan kuadrat adalah :
 |
| rumus abc |
Rumus abc ini bisa kita gunakan untuk mencari akar-akar persamaan kuadrat yang merupakan bilangan irrasional.
Contoh :
a. x² - 7x + 5=0
maka a=1, b=-7 dan c=5
b. 2x² + 8x + 7=0
maka a=2, b=6 dan c=11
Diskriminan adalah suatu nilai pembeda untuk menentukan jumlah dan jenis akar-akar persamaan kuadrat. Diskriminan suatu persamaan kuadrat ax²+ bx + c=0 dapat ditentukan dengan rumus berikut :
 |
| diskriminan |
- Jika D > 0, maka persamaan kuadrat mempunyai dua akar real yang berbeda. Jika digambar dalam bidang kartesius maka kurva persamaan kuadrat tersebut memotong sumbu x di dua titik. Persamaan kuadrat bisa difaktorkan.
- Jika D=0, maka persamaan kuadrat mempunyai dua akar real yang sama. Jika digambar dalam bidang kartesius maka kurva persamaan kuadrat tersebut menyinggung sumbu x di satu titik. Persamaan kuadrat bisa difaktorkan.
- Jika D < 0, maka persamaan kuadrat mempunyai dua akar yang tidak real. Jika digambar dalam bidang kartesius maka kurva persamaan kuadrat tersebut tidak memotong sumbu x. Persamaan kuadrat tidak bisa difaktorkan.
 |
| kurva dan diskriminan |
Contoh :
1. Tentukan nilai diskriminan dari persamaan berikut
a. x2 – 6x + 8=0
b. x2 + 7x – 10=0
c. 2x2 – 9x + 15=0
2. Tentukan jenis akar persamaan berikut
a. 4x² - 81=0
b. x² - 11x + 24=0
c. 2x²+ 7x + 9=0
Jawab :
1 a. x2 – 6x + 8=0
a=1, b=-6, c=8
D=b² - 4.a.c
=(-6)² - 4.1.8
=36 - 32
=4
b. x2 + 7x – 10=0
a=1, b=7, c=-10
D= b² - 4.a.c
=7² - 4.1.-10
=49 + 40
=89
c. 2x2 – 9x + 15=0
a=2, b=-9, c=15
D=b² - 4.a.c
=(-9)² - 4.2.15
=81 - 120
=- 39
2. a. x² - 6x +9=0
a=1, b=-6, c=9
D=b² - 4.a.c
=(-6)² - 4.1.9
=36 - 36
=0
D=0, akar-akarnya real dan sama
b. x² - 11x + 24=0
a=1, b=-11, c=24
D=b² - 4.a.c
=(-11)² - 4.1.24
=121 - 96
=125
D > 0, akar-akarnya real dan berbeda
c. 2x²+ 7x + 9=0
a=2, b=7, c=9
D=b² - 4.a.c
=7² - 4.2.9
=49 - 72
=-23
D < 0, akar-akarnya tidak real
Jumlah dan hasil kali akar-akar
Jika suatu persamaan kuadrat memiliki akar- akar x₁ dan x₂, maka kita dapatkan rumus-rumus berikut :
 |
| jumlah dan hasil kali akar |
Contoh :
Dari persamaan 3x2 – 11x + 6=0 tentukan nilai dari :
a. x₁²+x₂²
b. x₁ - x₂
Jawab :
a=3, b=-11, c=6
x₁+x₂=-b/a=11/3
x₁.x₂ =c/a=6/3
a. x₁²+x₂²=(x₁+x₂)² - 2x₁.x₂
=(11/3)² - 2. 6/3
=121/9 - 12/3
=121/9 - 36/9
=85/9
b. x₁ - x₂=√D/a
=√[(-11)²-4.3.6]/3
=√[121-72] /3
=√49/3
=7/3
Menentukan persamaan kuadrat jika diketahui akar-akarnya yaitu α dan β bisa dengan dua cara, yaitu :
1. x² - (α+β)x + αβ=0
2. (x - α) (x - β)=0
Contoh :
1. Tentukan persamaan kuadrat yang akar-akarnya adalah -2 dan 5
2. Tentukan persamaan kuadrat yang akar-akarnya kembar yaitu 3
3. Tentukan persamaan kuadrat baru yang akar-akarnya 2 kali dari persamaan 2x² -8x + 15
4. Jika akar-akar persamaan kuadrat x² -5x + 6=0 adalah x₁ dan x₂, tentukan persamaan kuadrat baru yang akar-akarnya (x₁ + 2) dan (x₂ + 2)
Jawab
1. α=-2 dan β=5
x² - (α+β)x + αβ=0
x² - (-2+5)x + (-2.5)=0
x² - 3x - 10=0
2. α=β=3
(x - α) (x - β)=0
(x - 3) (x - 3)=0
x² - 3x - 3x + 9=0
x² - 6x + 9=0
3. 2x² -8x + 15=0
x₁+x₂=-b/a=-8/2=-4
x₁.x₂ =c/a =15/2
α=2x₁ dan β=2x₂
α+β= 2x₁ + 2x₂
=2 (x₁+x₂)
=2 (-4)
= -8
αβ= 2x₁.2x₂
=4.x₁.x₂
=4. 15/2
=30
Persamaan baru
x² - (α+β)x + αβ=0
x² - (-8)x + 30=0
x² + 8x + 30=0
4. x² -5x + 6=0
x₁+x₂=-b/a=-5/1=-5
x₁.x₂ =c/a =6/2 =3
α=x₁ +2 dan β=x₂ + 2
α+β= x₁ +2 + x₂ + 2
= x₁+x₂ + 4
=-5 + 4
=-1
αβ=(x₁+2) (x₂+2)
= x₁.x₂ + 2(x₁+x₂) + 4
=3 + 2(-5) + 4
=3 - 10 + 4
=-3
Persamaan baru
x² - (α+β)x + αβ=0
x² - (-1)x + (-3)=0
x² + x - 3=0
Demikian materi persamaan kuadrat yang dapat kami uraikan.
Semoga bermanfaat