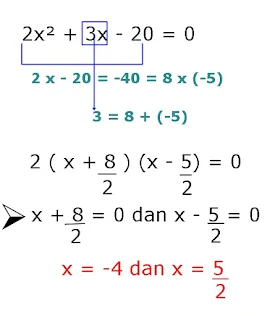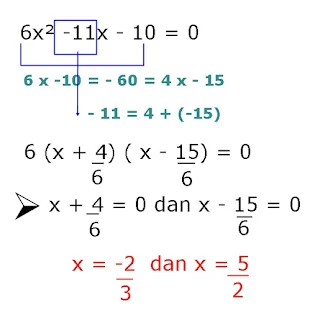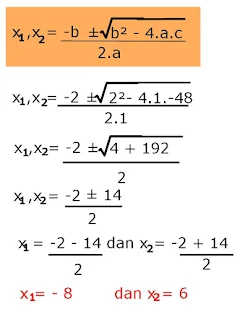Persamaan kuadrat sangat penting untuk dipahami karena bukan hanya digunakan untuk mencari penyelesaian dalam sebuah pelajaran matematika, tetapi juga dalam ilmu fisika, kimia maupun ekonomi. Dalam materi persamaan kuadrat kita harus menguasai cara mencari akar-akarnya untuk mendapatkan penyelesaian.
Ada tiga cara dalam mencari akar-akar persamaan kuadrat yaitu dengan cara memfaktorkan, melengkapkan kuadrat sempurna dan rumus abc. Untuk lebih memahaminya, kami sajikan soal-soal latihan berikut untukmu berlatih.
Tentukan akar-akar persamaan Kuadrat berikut dengan cara memfaktorkan !
1. x² - 16=0
Pembahasan :
rumus a² - b²=(a+b) (a-b)
x² - 16=0
x² - 4²=0
(x+4) (x-4)=0
➤ x + 4=0 dan x - 4=0
x=-4 dan x=4
2. 4x² - 81=0
Pembahasan :
rumus a² - b²=(a+b) (a-b)
4x² - 81=0
(2x)² - 9²=0
(2x + 9) (2x-9)=0
➤ 2x + 9=0 dan 2x - 9=0
2x=-9 dan 2x=9
x=-9/2 dan x=9/2
3. x² + 7x + 10=0
Pembahasan :
7=2 + 5
10=2 x 5
(x+2) (x+5)=0
➤ x + 2=0 dan x + 5=0
x=-2 dan x=-5
4. x² + 3x - 40=0
Pembahasan :
3=8 + (-5)
-40=8 x (-5)
(x + 8) dan (x - 5)=0
➤x + 8=0 dan x - 5=0
x=-8 dan x=5
5. x² - 3x - 28=0
Pembahasan :
-3=4 + (-7)
-28=4 x (-7)
(x+4) (x -7)=0
➤ x+4=0 dan x-7=0
x=-4 dan x=7
6. x² - 11x + 30=0
Pembahasan :
-11=-5 + (-6)
30 =-5 x (-6)
(x-5) (x-6)=0
➤ x - 5=0 dan x - 6=0
x=5 dan x=6
7. x² + 7x - 144=0
Pembahasan :
7=16 + (-9)
-144=16 x (-9)
(x+16) (x - 9)=0
➤ x + 16=0 dan x - 9=0
x=- 16 dan x=9
8. 2x² + 3x - 20=0
Pembahasan :
9. 3x² - 17x - 28=0
Pembahasan:
10. 6x² -11x - 10=0
Pembahasan :
Tentukan akar-akar persamaan kuadrat berikut dengan cara melengkapkan kuadrat sempurna !
1. x² + 6x + 8=0
Pembahasan :
x² + 6x + 8 =0 1. pindahkan konstanta ke ruas kanan
x² + 6x =- 8 2. kedua ruas ditambah (b/2)²
x² + 6x + 3²=-8 + 3² 3. ruas kiri diubah ke bentuk kuadrat sempurna
(x + 3)² =1 4. kedua ruas diakar
√(x + 3)² = √1
(x + 3) =± 1
➤ x + 3=-1 dan x + 3=1
x=-1 -3 dan x=1 - 3
x=-4 dan x=-2
2. x² - 8x + 15=0
Pembahasan :
x² - 8x + 15 =0
x² - 8x =-15
x² - 8x + (-4)²=-15 + (-4)²
(x - 4)² =1
x -4 =± 1
➤ x - 4=-1 dan x - 4=1
x=-1 +4 dan x=1 + 4
x=3 dan x=5
3. x² + 5x - 36=0
Pembahasan :
x² + 5x - 36 =0
x² + 5x =36
x² + 5x + (2,5)²=36 + (2,5)²
x² + 5x + (2,5)²=36 + 6,25
(x + 2,5)² =42,25
x + 2,5 =± 6,5
➤ x + 2,5=- 6,5 dan x + 2,5=6,5
x=- 6,5 - 2,5 dan x=6,5 - 2,5
x=- 9 dan x=4
4. 3x² - 10x + 8=0
Pembahasan :
3x² - 10x + 8 =0 1. bagi dengan a
x² - (10/3)x + 8/3 =0 2. pindahkan konstanta ke ruas kanan
x² - (10/3)x =- 8/3 3. kedua ruas ditambah (b/2)²
x² - (10/3)x +(-5/3)²=- 8/3 + (-5/3)² 4. ubah ke bentuk kuadrat sempurna
(x - 5/3)² =-24/9 + 25/9
(x - 5/3)² =1/9 5. kedua ruas diakar
x - 5/3 =± 1/3
➤ x - 5/3=-1/3 dan x -5/3=1/3
x=-1/3 + 5/3 dan x=1/3 + 5/3
x=4/3 dan x=6/3=2
5. 2x² - 5x - 42=0
Pembahasan :
2x² - 5x - 42 =0
x² - 5/2x - 21 =0
x² - 5/2x =21
x² - 5/2x + (-5/4)²=21 + (-5/4)²
(x - 5/4)² =336/16 + 25/16
(x - 5/4)² =361/16
(x - 5/4) =± 19/4
➤ x - 5/4=-19/4 dan x - 5/4=19/4
x=-19/4 + 5/4 dan x=19/4 + 5/4
x=-14/4=-3,5 dan x=24/4=6
Tentukan akar-akar persamaan kuadrat berikut dengan menggunakan rumus abc !
1. x² + 2x - 48=0
Pembahasan :
a=1, b=2 dan c=-48
2. x² - 12x + 27=0
Pembahasan :
a=1, b=-12 dan c=27
3. x² - 4x + 1=0
Pembahasan :
a=1, b=-4 dan c=1
4 2x² + x - 45=0
Pembahasan:
a=2, b=1 dan c=-45
5. 3x² - 17x + 20=0
Pembahasan :
a=3, b=-17 dan c=20
Semoga Bermanfaat