Logaritma adalah merupakan kebalikan (invers) dari bentuk eksponen. Materi logaritma mulai dipelajari pada Matematika peminatan kelas 10. Sudahkah kamu memahami sifat-sifat pada logaritma?
Pada kesempatan kali ini kita akan membahas latihan soal logaritma, semoga membantumu lebih memahami materi tersebut.
1. Pernyataan 2³=8 jika diubah ke dalam bentuk logaritma adalah....
a. ²log 3=8
b. ²log 8=3
c. ³log 2=8
d. ³log 8=2
Pembahasan :
2³=8 dalam bentuk logaritma ²log 8=3
2. Nilai dari ³log 9=....
a. 2
b. 3
c. 12
d. 27
Pembahasan :
³log 9=³log 3²
=2 x ³log 3
=2 x 1
=2
3. Nilai dari ²log 32 + ³log 27 - ⁵log 625=....
a. 2
b. 3
c. 4
d. 5
Pembahasan :
²log 32 + ³log 27 - ⁵log 625
= ²log 2⁵ + ³log 3³ - ⁵log 5⁴
=5 x ²log 2 + 3 x ³log 3 - 4 x ⁵log 5
=5 + 3 - 4
=4
4. Nilai dari ⁵log 0,04 + ²log (1/4) - ³log (1/81)=....
a. 0
b. 1
c. 2
d. -1
Pembahasan :
⁵log 0,04 + ²log (1/4) - ³log (1/81)
= ⁵log (1/25) + ²log (1/4) - ³log (1/81)
=⁵log 5⁻² + ²log 2⁻² - ³log 3⁻⁴
=-2 x ⁵log 5 + (-2)x ²log 2 - (-4)x ³log 3
=-2 + (-2) - (-4)
=0
5. Nilai dari ⁴log 32 + ⁹log 27=....
a. 2,5
b. 3
c. 3,5
d. 4
Pembahasan :
6. Nilai dari ³log √243=....
a. 2,5
b. 3,5
c. 4,5
d. 5,5
Pembahasan :
7. Diketahui ²log 3=1,6 dan ²log 5=2,3. Nilai dari ²log 90 adalah....
a. 5.5
b. 5.6
c. 6,5
d. 6,6
Pembahasan :
²log 90=²log (2x3x3x5)
=²log 2 + ²log 3 + ²log 3 + ²log 5
=1 + 1,6 + 1,6 + 2,3
=6,5
Pembahasan :
9. Jika log 2=a dan log 3=b, maka nilai dari log 45 adalah....
a. 5a + 2b
b. 2b + 1
c. 2b+1 - 5a
d. 2b+1 - a
Pembahasan :
log 45=log (3²x10 :2)=log 3²+log 10 - log 2=2 x log 3 + log 10 - log 2
=2b + 1 - a
10. Diketahui ²log 3=a dan ³log 7=b. Nilai ⁶log 98=....
a. (1+2b)/a
b. (1+2ab)/a
c. (1+2ab/(1+a)
d. (1+2ab)/ab
Pembahasan :
11. Himpunan penyelesaian dari ²log (x²- 7x + 18)=3 adalah....
a.{-2, -5}
b.{2,5}
c.{-3,5}
d.{3,6}
Pembahasan :
²log (x²- 7x + 18)= ²log 2³
(x²- 7x + 18)=8
x²- 7x + 18 - 8=0
x²- 7x + 10=0
(x-2) (x-5)=0
x=2 atau x=5
HP={2,5}
adalah....
a. 2
b. 3
c. 7
d. 9
Pembahasan :
a. 1
b. 2
c. 3
d. -2
Pembahasan :
14. Nilai dari ¹²⁵log 243 x ⁴log 25 x ³log 16=.....
a. 4/3
b. 15/2
c. 10/3
d. 20/3
Pembahasan :
Pembahasan :
16. Nilai x yang memenuhi persamaan log log x=log (3 - log x) + log 2 adalah.....
a. 2
b. 6
c. 50
d. 100
Pembahasan :
log log x=log (3 - log x) + log 2
log log x=log ((3 - log x) . 2)
log x=(3 - log x) . 2
log x=6 - 2.log x
log x + 2.log x=6
3.log x=6
log x=6:3=2
log x=log 10² x=100
17. Jika diketahui log (x+y)=2.log 2 dan log (x-y)=3.log 12 - 3.log 6, maka nilai dari xy adalah....
a.-12
b.-6
c. 6
d. 12
Pembahasan :
log (x+y)=2.log 2
log (x+y)=log 2²
log (x+y)=log 4
x+y =4 ..........(1)
log (x-y)=3.log 12 - 3.log 6log (x-y)=3(log 12 - log 6)
log (x-y)=3.log (12:6)
log (x-y)=3.log 2
log (x-y)=log 2³
x-y =8 ...........(2)
Eliminasi (1) dan (2)
x+y =4
x-y =8 +
2x =12
x =6
x+y =4
x-y =8 -
2y=-4
y=-2
maka xy=6(-2)=-12
adalah.....a.-2
b. 2
c. -2 dan 2
d. -1 dan 2
Pembahasan :
2x+5=(x+1)²
2x+5=x²+2x+1
0=x²+2x+1-2x-5
0=x²-4
0=(x+2) (x+2)
x=-2, x=2
syarat logaritma,
x+1 > 0
x > -1
maka x yang memenuhi adalah 2
19. Nilai x yang memenuhi pertidaksamaan
adalah....
a. ¼ < x < 64
b -4 < x < 64
c. 0 < x < ¼
d. 0< x < 64
Pembahasan :
²log x=-2 atau ²log x=6
²log x=²log 2⁻² atau ²log x=²log 2⁶
x=¼ atau x=64
maka ¼ < x < 64
20. Nilai x yang memenuhi adalah...
adalah...
a. 2 dan 6
b. hanya 2
c. hanya 6
d. 2 atau 6
Pembahasan :
➤ syarat 1
2x + 3 > 0
2x > -3
x > -3/2
➤ syarat 2
x² - 3x + 2 > 0
(x-1) (x-2) > 0
x < 1 atau x > 2
5x - 10 > 0
5x > 10
x > 2
➤ syarat 3
x² - 3x + 2 =5x - 10
x² - 3x - 5x + 2 + 10=0
x² - 8x + 12 =0
(x - 2) (x - 6) =0
x=2 atau x=6
➤ Nilai x yang memenuhi syarat 1, 2 dan 3 adalah hanya 6
Demikian beberapa latihan soal logaritma dan pembahasan yang dapat kami berikan. Semoga bermanfaat.
a.{-2, -5}
b.{2,5}
c.{-3,5}
d.{3,6}
Pembahasan :
²log (x²- 7x + 18)= ²log 2³
(x²- 7x + 18)=8
x²- 7x + 18 - 8=0
x²- 7x + 10=0
(x-2) (x-5)=0
x=2 atau x=5
HP={2,5}
adalah....
a. 2
b. 3
c. 7
d. 9
Pembahasan :
a. 1
b. 2
c. 3
d. -2
Pembahasan :
14. Nilai dari ¹²⁵log 243 x ⁴log 25 x ³log 16=.....
a. 4/3
b. 15/2
c. 10/3
d. 20/3
Pembahasan :
Pembahasan :
16. Nilai x yang memenuhi persamaan log log x=log (3 - log x) + log 2 adalah.....
a. 2
b. 6
c. 50
d. 100
Pembahasan :
log log x=log (3 - log x) + log 2
log log x=log ((3 - log x) . 2)
log x=(3 - log x) . 2
log x=6 - 2.log x
log x + 2.log x=6
3.log x=6
log x=6:3=2
log x=log 10² x=100
17. Jika diketahui log (x+y)=2.log 2 dan log (x-y)=3.log 12 - 3.log 6, maka nilai dari xy adalah....
a.-12
b.-6
c. 6
d. 12
Pembahasan :
log (x+y)=2.log 2
log (x+y)=log 2²
log (x+y)=log 4
x+y =4 ..........(1)
log (x-y)=3.log 12 - 3.log 6log (x-y)=3(log 12 - log 6)
log (x-y)=3.log (12:6)
log (x-y)=3.log 2
log (x-y)=log 2³
x-y =8 ...........(2)
Eliminasi (1) dan (2)
x+y =4
x-y =8 +
2x =12
x =6
x+y =4
x-y =8 -
2y=-4
y=-2
maka xy=6(-2)=-12
adalah.....a.-2
b. 2
c. -2 dan 2
d. -1 dan 2
Pembahasan :
2x+5=(x+1)²
2x+5=x²+2x+1
0=x²+2x+1-2x-5
0=x²-4
0=(x+2) (x+2)
x=-2, x=2
syarat logaritma,
x+1 > 0
x > -1
maka x yang memenuhi adalah 2
19. Nilai x yang memenuhi pertidaksamaan
adalah....
a. ¼ < x < 64
b -4 < x < 64
c. 0 < x < ¼
d. 0< x < 64
Pembahasan :
²log x=-2 atau ²log x=6
²log x=²log 2⁻² atau ²log x=²log 2⁶
x=¼ atau x=64
maka ¼ < x < 64
20. Nilai x yang memenuhi
a. 2 dan 6
b. hanya 2
c. hanya 6
d. 2 atau 6
Pembahasan :
➤ syarat 1
2x + 3 > 0
2x > -3
x > -3/2
➤ syarat 2
x² - 3x + 2 > 0
(x-1) (x-2) > 0
x < 1 atau x > 2
5x - 10 > 0
5x > 10
x > 2
➤ syarat 3
x² - 3x + 2 =5x - 10
x² - 3x - 5x + 2 + 10=0
x² - 8x + 12 =0
(x - 2) (x - 6) =0
x=2 atau x=6
➤ Nilai x yang memenuhi syarat 1, 2 dan 3 adalah hanya 6
Demikian beberapa latihan soal logaritma dan pembahasan yang dapat kami berikan. Semoga bermanfaat.










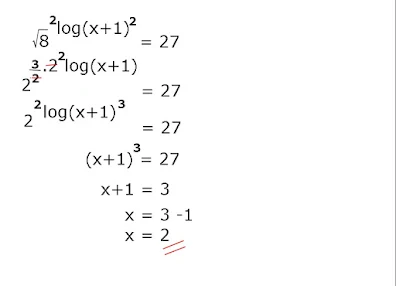








%20By%20Bimbel%20Jakarta%20Timur.webp)


