Pola bilangan adalah bagian dari materi barisan dan deret bilangan sebagai suatu susunan barisan bilangan yang membentuk pola yang teratur. Pola bilangan selain dipelajari pada kelas 8, juga seringkali digunakan dalam banyak soal ujian masuk perguruan tinggi maupun dalam ujian penerimaan pegawai.
Ada banyak jenis pola bilangan yang bisa kita pahami secara logika. Akan tetapi ada juga pola bilangan yang perlu kita ketahui rumus sukunya maupun jumlah deret bilangan dalam pola tersebut. Berikut ini adalah beberapa pola bilangan yang umumnya dipelajari.
1. Pola bilangan ganjil
Sesuai dengan namanya, pola bilangan ini adalah susunan bilangan ganjil berurutan dengan suku pertamanya adalah 1. Perhatikan pola jumlah lingkaran pada gambar di bawah ini!
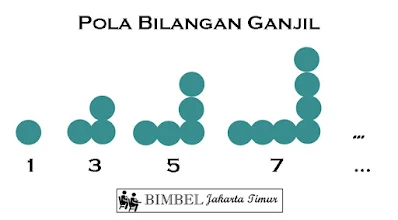 |
| Pola Bilangan Ganjil |
Bilangan ke-n kita tuliskan sebagai Un, maka bilangan pertama (U₁)=1, bilangan kedua (U₂)=3, bilangan ketiga (U₃) dan seterusnya. Bagaimana kita menentukan rumus suku ke-n (Un) pada pola bilangan ganjil?
Perhatikan bahwa dari U₁ ke U₂ ke U₃ dan seterusnya selalu bertambah 2. Maka kita tentukan sebagai berikut
U₁=1=2(1) - 1
U₂=3=2(2) - 1
U₃=5=2(3) - 1
sehingga
Un=2n - 1
Contoh soal
a. Tentukan bilangan ganjil ke 25 !
Jawab :
U₂₅=2(25) -
=50 - 1
=49
b. 99 adalah bilangan ganjil ke berapa?
Jawab :
2n - 1=99
2n =99 + 1
2n =100
n =100 : 2
n =50
Sekarang mari kita pelajari cara mencari rumus jumlah deret bilangan ganjil melalui contoh berikut!
a. Nilai dari 1 + 3 + 5 + 7 + ... + 15=....
Jawab :
Pertama tentukan dulu 15 adalah suku ke berapa dari pola bilangan ganjil dengan rumus Un=2n - 1
2n - 1=15
2n =15 + 1
2n =16
n =16 : 2=8
Perhatikan uraian berikut !
Jumlah seluruhnya adalah 16 x 4=64
Dari jawaban di atas kita bisa tentukan rumus jumlah n suku pertama bilangan ganjil (Sn)
angka 16 didapat dari 1 + 15 yaitu U₁ + U₈
angka 4 didapat dari 8 : 2 yaitu n : 2
Maka jumlah 8 bilangan ganjil
=16 x 4
=16 x 8 : 2
=(U₁ + U₈) x 8 : 2
Jumlah n bilangan adalah
Sn=(U₁ + Un) x n : 2
b. Tentukan jumlah 11 bilangan ganjil pertama
Jawab :
U₁₁=2(11) - 1=21
S₁₁=(U₁ + U₁₁) x 11 : 2
=(1 + 21) x 11 : 2
=22 x 11 : 2
=11 x 11
=121
Karena 121=11² maka bisa kita simpulkan bahwa
S₁₁=11² dan rumus jumlah n bilangan ganjil pertama adalah Sn=n²
2. Pola bilangan genap
Perhatikan pola jumlah lingkaran pada gambar berikut !
 |
| Pola Bilangan Genap |
Pola bilangan genap adalah 2 , 4 , 6, 8 dan seterusnya. Seperti juga bilangan ganjil, bilangan genap memiliki selisih dari satu bilangan ke bilangan berikutnya sebesar 2. Sekarang mari kita tentukan rumus suku ke-n bilangan genap.
U₁=2= 2(1)
U₂=4= 2(2)
U₃=6= 2(3)
Sehingga
Un=2n
Contoh soal
a. Tentukan bilangan genap ke 50 !
Jawab :
Un=2n
U₅₀=2(50)=100
b. Tentukan jumlah 10 bilangan genap pertama !
Jawab :
U₁₀=2(10)=20
Sama seperti pada pola bilangan genap, jumlah n bilangan adalah
Sn=(U₁ + Un) x n : 2
S₁₀=(U₁ + U₁₀) x 10 : 2
=(2 + 20) x 10 : 2
=22 x 10 : 2
=110
Dari jawaban soal di atas bisa kita tentukan rumus jumlah n bilangan genap pertama adalah
S₁₀=110
=10 x 11
Sn=n x (n+1)
3. Pola bilangan segitiga
Perhatikan pola jumlah lingkaran pada gambar berikut !
 |
| Pola Bilangan Segitiga |
Pola bilangan segitiga adalah 1, 3, 6, 10, ...
Untuk menentukan rumus pola bilangan segitiga, kita harus ingat terlebih dahulu rumus luas segitiga yaitu alas x tinggi : 2. Alas kita misalkan dengan n dan tinggi adalah (n+1), maka rumus bilangan ke n dari pola segitiga adalah
Un=n x (n+1) : 2
U₁=1 x (1+1) : 2=1 x 2 : 2=1
U₂=2 x (2+1) : 2=2 x 3 : 2=3
U₃=3 x (3+1) : 2=3 x 4 : 2=6
dan seterusnya
Contoh soal
a. Tentukan bilangan ke 7 dari pola bilangan segitiga
Jawab :
U₇=7 x (7+1) : 2
=7 x 8 : 2
=28
b. Suatu bilangan adalah anggota pola bilangan segitiga. Jika bilangan tersebut adalah 78, maka bilangan tersebut merupakan bilangan ke berapa?
Jawab :
Un =n x (n+1) : 2
78 =(n² + n) : 2
78 x 2 = n² + n
156 = n² + n
0 = n² + n - 156
0 =(n+13) (n-12)
n+13=0 atau n-12=0
n=- 13 atau n=12
nilai yang memenuhi adalah 12 karena positif
Rumus jumlah n bilangan segitiga adalah Sn=¹/₆ (n+1) (n+2)
4. Pola bilangan persegi
Perhatikan pola jumlah persegi kecil pada gambar berikut !
 |
| Pola Bilangan Persegi |
Pola bilangan persegi adalah 1, 4, 9, 16, ...
U₁=1=1²
U₂=4=2²
U₃=9=3²
U₄=16=4²
maka rumus bilangan ke-n pada pola bilangan persegi adalah sesuai dengan rumus persegi yaitu sisi x sisi atau s²
Un=n²
Sedangkan rumus jumlah n bilangan persegi adalah Sn= ¹/₆ (n+1) (2n+2)
Contoh soal
Tentukan bilangan ke 15 dari pola bilangan 1, 4, 9, ....
Jawab :
Un=n²
U₁₅=15²
=225
5. Pola bilangan persegipanjang
Perhatikan pola jumlah persegi kecil pada gambar berikut !
 |
| Pola Bilangan Persegi Panjang |
Pola bilangan persegi panjang adalah 2, 6, 12, 20, ....
Jika pola di atas kita sesuaikan dengan rumus luas persegi panjang yaitu Luas=panjang x lebar, maka
U₁=2 =1 x 2
U₂=6 =2 x 3
U₃=12=3 x 4
U₄=20=4 x 5
Sehingga Un= n x (n+1)
Sedangkan rumus jumlah n bilangan persegi panjang adalah
Sn=¹/₃ (n+1) (n+2)
Contoh soal
Suku ke n dari pola bilangan 2, 6, 12, 20, ... adalah 380. Tentukan nilai n!
Jawab :
Un =n x (n+1)
380=19 x 20
maka nilai n=19
6. Pola bilangan pangkat tiga (kubik)
Perhatikan pola jumlah kubus satuan pada gambar berikut !
 |
| Pola Bilangan Pangkat Tiga |
Pola bilangan pangkat tiga adalah 1, 8, 27, ....
U₁=1 =1³
U₂=8 =2³
U₃=27=3³
maka Un=n³
Contoh :
Bilangan ke 11 dari pola bilangan pangkat tiga adalah 11³=1331
7. Pola bilangan Pascal
Pola segitiga Pascal ditemukan oleh ilmuwan Perancis bernama Blaise Pascal. Pola ini sangat unik karena dapat diaplikasikan dalam banyak materi matematika. Untuk lebih jelasnya perhatikan polanya seperti di bawah ini.
Bilangan- bilangan pada tiap baris segitiga Pascal menunjukkan koefisien ekspansi bilangan cacah binomial.
(a + b)⁰=1
(a + b)¹=1.a + 1.b
(a + b)²=1.a² + 2.a.b + 1.b²
(a + b)³=1.a³ + 3.a².b + 3.a.b² + 1.b³
(a + b)⁴=1.a⁴ + 4.a³.b + 6.a².b² + 4.a.b³ + 1.b⁴
dan seterusnya
Pola jumlah bilangan segitiga Pascal pada baris ke n adalah 2n-1
Contoh
a. Tentukan koefisien x³y³ dari hasil penjabaran (x - y)⁶
Jawab :
(x - y)⁶=1.x⁶ - 6.x⁵y + 15.x⁴.y² - 20.x³y³ + 15.x²y⁴ - 6.x.y⁵ + 1.y⁶
➤ tanda (+) dan(-) berselang-seling
maka koefisien dari x³y³ adalah -20
b. Tentukan jumlah bilangan Pascal pada baris ke 8
jumlah bilangan Pascal pada baris ke 8 adalah 28-1=27=128
 |
| Pola Bilangan Pascal |
Bilangan- bilangan pada tiap baris segitiga Pascal menunjukkan koefisien ekspansi bilangan cacah binomial.
(a + b)⁰=1
(a + b)¹=1.a + 1.b
(a + b)²=1.a² + 2.a.b + 1.b²
(a + b)³=1.a³ + 3.a².b + 3.a.b² + 1.b³
(a + b)⁴=1.a⁴ + 4.a³.b + 6.a².b² + 4.a.b³ + 1.b⁴
dan seterusnya
Sekarang kita coba analisa cara menentukan jumlah bilangan Pascal pada suatu baris tertentu.
Baris pertama=1 =2⁰ = 21-1Pola jumlah bilangan segitiga Pascal pada baris ke n adalah 2n-1
Contoh
a. Tentukan koefisien x³y³ dari hasil penjabaran (x - y)⁶
Jawab :
(x - y)⁶=1.x⁶ - 6.x⁵y + 15.x⁴.y² - 20.x³y³ + 15.x²y⁴ - 6.x.y⁵ + 1.y⁶
➤ tanda (+) dan(-) berselang-seling
maka koefisien dari x³y³ adalah -20
b. Tentukan jumlah bilangan Pascal pada baris ke 8
jumlah bilangan Pascal pada baris ke 8 adalah 28-1=27=128
8. Pola bilangan Fibonacci
Pola bilangan Fibonacci pertama kali dipelajari oleh Leonardo da Pisa. Ayah beliau yang bernama William da Pisa dikenal dengan sebutan Bonacci, sehingga Leonardo da Pisa disebut Fibonacci yang merupakan singkatan dari filius Bonacci yang artinya anak dari Bonacci.
Pola bilangan Fibonacci adalah suatu pola di mana suku ke-n barisan itu merupakan jumlah dari dua suku sebelumnya yaitu suku ke-(n-1) dan suku ke-(n-2). Pola bilangan Fibonacci biasa ditulis dengan dua suku pertama lalu suku ketiga yang merupakan jumlah dari suku pertama dan kedua sehingga kita bisa kita tentukan suku-suku berikutnya.
Contoh soal
Tentukan tiga suku berikutnya dari barisan Fibonacci berikut !
a. 1, 1, 2, ...
b. 1, 3, 4, ...
Jawab :
a. 1, 1, 2, 3, 5, 8
Pola bilangan Fibonacci adalah suatu pola di mana suku ke-n barisan itu merupakan jumlah dari dua suku sebelumnya yaitu suku ke-(n-1) dan suku ke-(n-2). Pola bilangan Fibonacci biasa ditulis dengan dua suku pertama lalu suku ketiga yang merupakan jumlah dari suku pertama dan kedua sehingga kita bisa kita tentukan suku-suku berikutnya.
Contoh soal
Tentukan tiga suku berikutnya dari barisan Fibonacci berikut !
a. 1, 1, 2, ...
b. 1, 3, 4, ...
Jawab :
a. 1, 1, 2, 3, 5, 8
b. 1, 3, 4, 7, 11, 18
Demikian macam-macam pola bilangan yang dapat kami berikan pada artikel ini. Selain pola-pola bilangan di atas, masih ada barisan aritmatika, barisan geometri yang telah kami bahas sebelumnya dalam artikel Barisan Dan Deret.
SEMOGA BERMANFAAT


