Salah satu materi Bimbel Jakarta Timur yang diajarkan di kelas 9 adalah tentang bangun ruang sisi lengkung. Bangun ruang sisi lengkung adalah kelompok bangun ruang.
Kelompok bangun ruang yang memiliki bagian-bagian dan selimut yang berbentuk lengkungan. Di antara yang termasuk ke dalam bangun ruang sisi lengkung adalah tabung, kerucut, dan bola.
Berikut adalah contoh soal dan pembahasannya.
Bangun Ruang sisi lengkung
1. Diketahui tabung dengan diameter 7 cm dan tinggi12 cm. Tentukan :
a. Volume tabung
b. Luas permukaan tabung
Pembahasan
Diketahui : d = 7 cm, maka r =3,5 cm
t = 12 cm
a. Volume tabung = π x r² x t
= 22/7 x 3,5² x 12
= 462 cm³
b. Luas permukaan = 2 π r (r + t)
= 2 x 22/7 x 3,5 ( 3,5 + 12 )
= 22 x 15,5
= 341 cm²
2. Luas selimut tabung yang tingginya 15 cm adalah 471 cm2.
Tentukan volume tabung ! ( π=3,14)
Pembahasan :
Diketahui : t = 15 cm
Ls = 471 cm²
Tentukan dulu panjang jari-jari dari rumus luas selimut tabung
Luas selimut = 471
2 x π x r x t = 471
2 x 3,14 x r x 15 = 471
94,2 x r = 471
r = 471 : 94,2
r = 5 cm
Maka volume tabung didapat,
Volume= π x r² x t
=3,14 x 5² x 15
=1.177,5 cm³
Pembahasan
Diketahui : d = 21 cm, maka r = 10,5 cm
V = 13.860 cm³
Tentukan dulu tinggi tabung dari rumus volume
Volume =13.860
π x r² x t=13.860
22/7 x 10,5² x t = 13.860
346,5 x t = 13.860
t = 13.860 : 346,5
t = 40
Luas permukaan tabung tanpa tutup adalah
Luas permukaan= π x r (r +2t)
= 22/7 x 10,5 x (10,5 + 2.40)
= 33 (10,5 + 80)
= 33 x 90,5
= 2.986,5 cm²
a. Tinggi kerucut
Pembahasan
Diketahui : r = 7 cm
s = 25 cm
a. t² = s² - r²
= 25² - 7²
= 625 - 49
=576
t = 24 cm
b. Volume =1/3 x π x r² x t
=1/3 x 22/7 x 7² x 24
=1.232 cm³
a. Volume kerucut
Pembahasan
Diketahui : r = 6 cm
t = 8 cm
a. Volume = 1/3 x π x r² x t
= 1/3 x 3,14 x 6² x 8
= 301,44 cm³
b. Tentukan dulu panjang garis pelukis
s² = r² + t²
= 6² + 8²
= 36 + 64
= 100
s = 10
Maka luas permukaan kerucut
Lp = п x r (r + s)
= 3,14 x 6 (6 + 10)
= 301,44 cm²
Pembahasan
Diketahui : r =8 cm
Ls =427,04 cm2
Tentukan dulu garis pelukis dan tinggi kerucut dari rumus luas selimut
Luas selimut = 427,04
п x r x s = 427,04
3,14 x 8 x s = 427,04
25,12 x s = 427,04
s = 427,04 : 25,12
s = 17 cm
t² = s² - r²
= 17² - 8²
= 289 - 64
= 225
t =15 cm
Volume = 1/3 x π x r² x t
= 1/3 x 3,14 x 8² x 15
= 1.004,8 cm³
a. Volume bola
Pembahasan
Diketahui : r = 15 cm
a. Volume = 4/3 x π x r³
= 4/3 x 3,14 x 15³
= 14.130 cm³
b. Luas permukaan = 4 x π x r²
= 4 x 3,14 x 15²
= 2.826 cm²
Pembahasan
Diketahui : V = 38.808 cm³
Menentukan panjang jari-jari terlebih dahulu
Volume = 38.808
4/3 x π x r³ =38.808
4/3 x 22/7 x r³=38.808
r³ =38.808 x 3/4 x 7/22
r³ =9.261
r =21 cm
Luas permukaan bola= 4 x π x r²
=4 x 22/7 x 21²
=5.544 cm²
Pembahasan
Diketahui : Luas belahan bola padat= 942 cm2
Belahan bola padat memiliki luas permukaan yaitu setengah belahan bola dan luas di belahannya yang berupa luas lingkaran. Sehingga luas permukaan keseluruhan adalah :
(2 x л x r²) + (п x r² )=3 x π x r²
3 x π x r² = 942
3 x 3,14 x r² = 942
9,42 x r² = 942
r² = 942 : 9,42
r² = 100
r = 10 cm
Volume bola = 4/3 x π x r³
= 4/3 x 3,14 x 10³
= 4.186,67 cm³
Diketahui : t = 15 cm
Ls = 471 cm²
Tentukan dulu panjang jari-jari dari rumus luas selimut tabung
Luas selimut = 471
2 x π x r x t = 471
2 x 3,14 x r x 15 = 471
94,2 x r = 471
r = 471 : 94,2
r = 5 cm
Maka volume tabung didapat,
Volume= π x r² x t
=3,14 x 5² x 15
=1.177,5 cm³
3. Sebuah tabung tanpa tutup memiliki diameter 21cm dan volume 13.860 cm3. Tentukan luas permukaan tabung tersebut ! (π=22/7)
Pembahasan
Diketahui : d = 21 cm, maka r = 10,5 cm
V = 13.860 cm³
Tentukan dulu tinggi tabung dari rumus volume
Volume =13.860
π x r² x t=13.860
22/7 x 10,5² x t = 13.860
346,5 x t = 13.860
t = 13.860 : 346,5
t = 40
Luas permukaan tabung tanpa tutup adalah
Luas permukaan= π x r (r +2t)
= 22/7 x 10,5 x (10,5 + 2.40)
= 33 (10,5 + 80)
= 33 x 90,5
= 2.986,5 cm²
4. Sebuah kerucut mempunyai panjang jari-jari 7 cmdan garis pelukis 25 cm. Tentukan :
a. Tinggi kerucut
b. Volume kerucut
Pembahasan
Diketahui : r = 7 cm
s = 25 cm
a. t² = s² - r²
= 25² - 7²
= 625 - 49
=576
t = 24 cm
b. Volume =1/3 x π x r² x t
=1/3 x 22/7 x 7² x 24
=1.232 cm³
5. Jika panjang jari-jari sebuah kerucut adalah 6 cm dan tingginya 8 cm, tentukan :
a. Volume kerucut
b. Luas permukaan kerucut
Pembahasan
Diketahui : r = 6 cm
t = 8 cm
a. Volume = 1/3 x π x r² x t
= 1/3 x 3,14 x 6² x 8
= 301,44 cm³
b. Tentukan dulu panjang garis pelukis
s² = r² + t²
= 6² + 8²
= 36 + 64
= 100
s = 10
Maka luas permukaan kerucut
Lp = п x r (r + s)
= 3,14 x 6 (6 + 10)
= 301,44 cm²
6. Luas selimut kerucut dengan jari-jari 8 cmadalah 427,04 cm2.. Jika π =3,14, maka tentukan volume kerucut tersebut!
Pembahasan
Diketahui : r =8 cm
Ls =427,04 cm2
Tentukan dulu garis pelukis dan tinggi kerucut dari rumus luas selimut
Luas selimut = 427,04
п x r x s = 427,04
3,14 x 8 x s = 427,04
25,12 x s = 427,04
s = 427,04 : 25,12
s = 17 cm
t² = s² - r²
= 17² - 8²
= 289 - 64
= 225
t =15 cm
Volume = 1/3 x π x r² x t
= 1/3 x 3,14 x 8² x 15
= 1.004,8 cm³
7. Sebuah bola memiliki panjang jari-jari 15 cm. Jika π=3,14, maka tentukan :
a. Volume bola
b. Luas permukaan bola
Pembahasan
Diketahui : r = 15 cm
a. Volume = 4/3 x π x r³
= 4/3 x 3,14 x 15³
= 14.130 cm³
b. Luas permukaan = 4 x π x r²
= 4 x 3,14 x 15²
= 2.826 cm²
8. Sebuah bola volumenya 38.808 cm3.Jika π=22/7 , tentukan luas permukaan bola tersebut!
Pembahasan
Diketahui : V = 38.808 cm³
Menentukan panjang jari-jari terlebih dahulu
Volume = 38.808
4/3 x π x r³ =38.808
4/3 x 22/7 x r³=38.808
r³ =38.808 x 3/4 x 7/22
r³ =9.261
r =21 cm
Luas permukaan bola= 4 x π x r²
=4 x 22/7 x 21²
=5.544 cm²
9. Belahan setengah bola padat memiliki luas permukaan 942 cm2. Jika π=3,14, tentukan volume bola tersebut !
Pembahasan
Diketahui : Luas belahan bola padat= 942 cm2
Belahan bola padat memiliki luas permukaan yaitu setengah belahan bola dan luas di belahannya yang berupa luas lingkaran. Sehingga luas permukaan keseluruhan adalah :
(2 x л x r²) + (п x r² )=3 x π x r²
3 x π x r² = 942
3 x 3,14 x r² = 942
9,42 x r² = 942
r² = 942 : 9,42
r² = 100
r = 10 cm
Volume bola = 4/3 x π x r³
= 4/3 x 3,14 x 10³
= 4.186,67 cm³
 |
| Soal Nomer 10 |
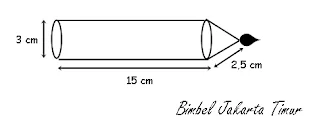
10. Sebuah lilin seperti gambar di samping berbentuk gabungan tabung dan kerucut.
Jika lilin terbakar 3 cm3 setiap menit, berapa lama lilin akan habis terbakar?
Pembahasan
Diketahui : r tabung=r kerucut=3 cm : 2=1,5 cm
t tabung=15 cm
s kerucut=2,5 cm
kecepatan pembakaran=3 cm³/menit
Mencari tinggi kerucut
t² = s² - r²
= 2,5² - 1,5²
= 6,25 - 2,25 = 4
t = 2 cm
Volume lilin = volume tabung + volume kerucut
= ( π x r² x t ) + (1/3 x π x r² x t)
= 105,975 + 4,71
= 110,685 cm³
Waktu yang dibutuhkan = 110,685 : 3
= 36,895 menit dibulatkan menjadi 37 menit
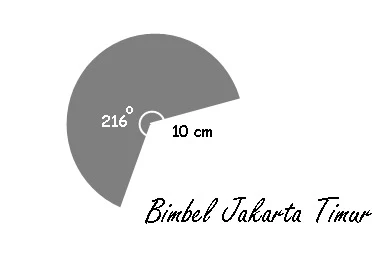
11. Sebuah selimut kerucut dibuat dari kertas karton berbentuk juring dengan sudut 216o dan jari-jari 10 cm. Tentukan jari-jari kerucut yang terbentuk dan volumenya !
Perhatikan gambar di samping !
 |
| Soal Nomer 11 |
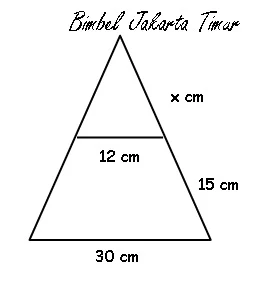
12.Sebuah kap lampu terbuat dari bentuk potongan kerucut seperti gambar. Jika diameter atas 12 cm dan diameter bawah adalah 30 cm, tentukan luas permukaan kap lampu !
Pembahasan
Perhatikan gambar berikut sebagai sketsa kerucut !
 |
| Soal Nomer 12 |
Tentukan nilai x sebagai garis pelukis kerucut kecil dengan menggunakan kesebangunan.
13. Sebuah bak air berbentuk tabung dengan jari-jari16 cm dan tinggi 40 cm akan diisi air menggunakan wadah berbentuk belahan bola yang jari-jarinya 8 cm. Berapa kali air harus dituang dari wadah supaya bak air penuh?
Pembahasan
Diketahui : tabung r = 16 cm, t = 40 cm
belahan bola r = 8 cm
Banyaknya volume belahan bola yang harus dituang
= Volume tabung : volume belahan bola
= ( п x r² x t ) : (1/2 x 4/3 x п x r³)
= (r² x t ) : (2/3 x r³)
= 16² x 40 x 3/2 : 8³
= 30 kali
14. Sebuah bandul terbentuk dari kerucut dan belahan bola dengan panjang jari-jari 3 cm. Jika tinggi kerucut 4 cm, tentukan luas permukaan dan volume bandul tersebut!
Pembahasan
Diketahui : r kerucut = r bola = 3 cm
t kerucut = 4 cm
Menentukan garis pelukis kerucut
s² = r² + t²
s² = r² + t²
= 3² + 4²
= 9 + 16
= 25
s = 5 cm
Luas permukaan bandul
= Luas kerucut + luas belahan bola
= (п x r x s) + (2 x п x r²)
= п x r x (s + 2r)
= 3,14 x 3 (5 + 6)
= 103,62 cm²
Volume bandul
= volume kerucut + volume belahan bola
= (1/3 x п x r²x t) + (2/3 x п x r³)
= 1/3 п x r² (t + 2r)
= 1/3 x 3,14 x 9 (4 +6)
= 94,2 cm³
Contoh soal bandul :
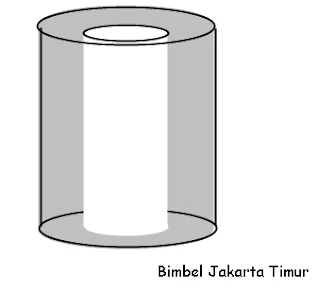
15. Gambar di samping adalah sebuah saluran air yang terbuat dari beton yang berlubang di dalamnya. Panjang jari-jari luar 15 cm, jari-jari dalam 10 cm dan tingginya 50 cm.
Jika berat 1 cm3 adalah 5 gram, berapa kilogram berat saluran air tersebut?
Pembahasan
Diketahui r besar = 15 cm
r kecil = 10 cm
t = 50 cm
berat 1 cm³ = 5 gram
Volume saluran air
= Volume tabung besar - volume tabung kecil
= (п x rb²x t) - (п x rk² x t)
= п x t (rb² - rk²)
= 3,14 x 50 (15² - 10²)
= 157 (225 - 100)
= 19.625 cm³
Berat beton = volume x 5 gram
= 19.625 x 5
= 98.125 gram
= 98,125 kg





%20By%20Bimbel%20Jakarta%20Timur.webp)



